Photonics Modeling: Optical Ising machines solve complex engineering, science, and even business problems
DAVIDE PIERANGELI, GIULIA MARCUCCI, and CLAUDIO CONTI
Combinatorial optimization problems are ubiquitous in science, engineering, and business. Examples include resource allocation, community detection, and bitcoin generation. In the traveling salesman problem, for example, a traveler planning his or her trip tries to find the shortest route to visit a given list of many cities. To find the optimal solution, the traveler must compare all possible paths—a computation that becomes exponentially harder as the number of cities increases.
Sudoku, the popular combinatorial number-placement puzzle, is another difficult problem. While it is easy to verify if all the numbers are in place, finding the solution can take an extremely long time, even for an experienced player. On large scales (that is, with several thousands of variables), these combinatorial problems cannot be efficiently solved by modern electronic computers, prompting researchers to explore novel approaches.
One strategy is to map all the relevant problems to a particular problem—named “NP-complete”—that can be efficiently solved by dedicated hardware. An intensely studied NP-complete problem is a system of interacting classical spins called an Ising model. Ising machines, as they are known, are special-purpose processors that solve the Ising model.
Recently, much effort by several researchers worldwide is aimed at developing a photonic version of an Ising machine that can exploit the unique wave properties of light: high speed, parallelization, and energy efficiency. To date, optical Ising machines can tackle computations with a few thousand spins.
A research group at the University of Rome La Sapienza has now realized the largest optical Ising machine to date by using active display technology to represent more than 10,000 spins with a spatially modulated light field.1, 2 Compared to existing Ising machines, our device can be further scaled to accommodate many more spins. With larger and programmable Ising machines, researchers could potentially tackle complex optimization problems like determining a protein’s structure based on its amino acid sequence.
How does a photonic Ising machine work?
The Ising model, first considered by physicists Wilhelm Lenz and Ernst Ising in 1920 to model magnetic materials, describes a network of interacting spins that can point only in two directions—up or down. The energy of spin depends on the interaction with the others’ spins.
In a ferromagnet, neighboring spins have all the same couplings and will prefer to align in the same direction. In a spin glass, all the spins are randomly coupled and align in disordered configurations in many different states with very similar energy. An Ising machine finds the spin configuration that minimizes the energy of the interacting spins and can be programmed for specific Ising problems, as ferromagnets or spin glasses.
The machine evolves towards the optimal spin state, which is the outcome of the computation. This solution, by a proper mathematical procedure, also furnishes the optimal solution of some other hard optimization problems.
Optical Ising machines use the phase of light fields to encode the spin configuration. The phase of the wave in a given spatiotemporal point is a spin 1 if the phase is 0, or is a spin -1 if the phase is π. Therefore, to implement a photonic Ising machine, three key ingredients are necessary: 1) binary optical degrees of freedom, such as the phases in a train of pulses; 2) a wave-mixing mechanism that provides programmable linear couplings between spins; and 3) low temperature (low noise) to ensure that the observed spin configuration corresponds to the desired solution.
Optical Ising machines can be much faster than similar machines realized by ultracold atoms, polaritons, or nanomagnets, as they can potentially process information at the speed of light and are inherently parallel with multiple spatial and frequency channels. They also take advantage of passive components for mathematical operations such as large matrix multiplications and Fourier transforms at fixed energy cost. Quantum optical Ising machines are also possible by using non-classical states of light.
Photon-based Ising machines have been developed using networks of time-multiplexed optical parametric oscillators.3, 4 Promising alternative photonic platforms are nanophotonic circuits, optical fiber, and free-space optical networks.5-7 These photonic machines have been used to solve very difficult optimization problems and to study the complex phases of spin glass systems.8 So far, however, these prototypes have not been scalable beyond a few hundred or a few thousand spins.
The effects of decoherence and dispersion limit hardware are based on pulses in optical cavities, as in the “coherent Ising machine.” Integrated optical circuits as directional couplers and phase modulators make the scaling to large numbers of spins very demanding. Realizing a large-scale, all-optical Ising machine is currently one of the most important open challenges in photonic computing.
Large-scale Ising machine by spatial light modulation
A different and innovative perspective to perform optical computing uses the spatial degrees of freedom of light. This proof-of-principle optical Ising machine breaks previous size records and relies on a highly scalable technology. The spatial-photonic processor handles tens of thousands of spins—and possibly more.
By using spatial multiplexing, the machine encodes and processes the spins and their interactions all at once by surprisingly simple free-space optics. This approach avoids complex optical fabrication requirements and eliminates assembly of numerous tiny components.
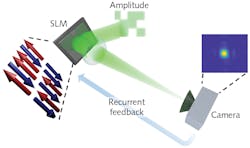
The critical element in the system is a spatial light modulator (SLM)—an active display that locally changes the phase of the optical field. This technological solution takes advantage of the massive parallelization and high-pixel densities of modern technology for light modulation: high-resolution SLMs contain millions of pixels in 1 cm. Each pixel may encode a spin, and groups of pixels act as a reconfigurable optical computation unit.
In the experimental setup, the SLM imprints a phase of 0 or p on distinct spatial points of the wavefront of a laser beam (see Fig. 1). The interaction between the optical spins is set by spatially modulating the beam intensity and occurs through optical propagation by linear interference.
To run the machine, researchers use a recurrent strategy (Roques-Carmes et al. have recently proposed this general type of architecture for evolving the spins). In its present realization, an intensity-modulated laser beam impinges on the SLM, where the spins are encoded as a binary phase pattern. The shaped beam propagates in free space, and its intensity distribution is detected on a camera. At each step, the spin configuration is updated to optimize the intensity detected in a single point, corresponding to energy minimization of the spin system. After many cycles, the optical field becomes stationary, and the spin configuration that corresponds to the ground state is obtained by simply reading the phases on the SLM.
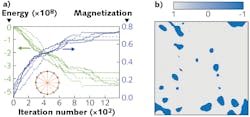
In the initial experimental demonstration, the spin interactions were first considered for a simple ferromagnet and machine outputs for different realizations of 40,000 spins all-to-all positively coupled were revealed (see Fig. 2). The initial random spin distribution under recurrent feedback evolves to a configuration having maximum magnetization and minimum energy. In a ground-state solution, analysis of the distribution of the spin clusters can prove that the machine yielded the ground state expected at low temperature from theoretical calculations. Various noise sources in the experiment determine the temperature.To demonstrate that the spin interaction can be tuned, a second set of experiments were performed. In this case, the spin couplings were adjusted to simulate an optical neural network known as Mattis spin glass. By larger wavefronts, we analyzed how physical observables like the phase’s magnetization and correlation lengths scaled with the number of spins using up to 75,076 spins—a machine size at least one order of magnitude larger than in any other previous system.
Current progress and connections with deep learning
In addition to being the physically biggest ever developed, this Ising machine is ready for further developments in scalability to tackle complex optimization problems on a large scale. Parallel processing of a further increasing number of spins can be obtained by using larger laser wavefronts and SLMs.
One exciting feature of the proposed computing architecture is the use of intrinsic optical noise as a controllable temperature for photonic simulations of phase transition phenomena. The idea of using dynamic noise to find optimal solutions more efficiently has recently been used to investigate phase transitions and complex phases of spin systems.9 An Ising machine can be a form of dynamic artificial neural network that is recurrently trained to identify a target ground state, linking the machine to deep learning. This artificial intelligence (AI) paradigm relies on several large-scale matrix multiplications—operations that occur at low power and high speed on an optical processor like an Ising machine (see Fig. 3).For these applications, the SLM of the machine should operate at higher speed. With the most recent active display technologies, the iteration time reduces computations to hundreds of microseconds. On the other hand, broader applications will require the inclusion of wave-mixing devices along the optical path and more involved architectures. For example, an effective “bias” magnetic field on the spins is needed to map the Ising model to the traveling salesman problem.
But even with these open challenges, the demonstration of novel and scalable photonic computing devices like this have brought optical Ising machines closer to solving real-world problems. The fascinating journey towards a large-scale all-optical Ising machine has now begun.
REFERENCES
1. D. Pierangeli, G. Marcucci, and C. Conti, Phys. Rev. Lett., 122, 213902 (2019).
2. C. Roques-Carmes and M. Soljačić, Physics, 12, 61 (2019).
3. P. L. McMahon et al., Science, 354, 6312, 614–617 (2016).
4. T. Inagaki et al., Science, 354, 6312, 603–606 (2016).
5. Y. Shen et al., Nat. Photonics, 11, 441–446 (2017).
6. K. Wu et al., J. Light Sci. Appl., 3, 2, e147 (2014).
7. R. Hamerly et al., Phys. Rev. X, 9, 021032 (2019).
8. D. Pierangeli et al., Nat. Commun., 8, 1501 (2017).
9. C. Roques-Carmes et al., arxiv:1811.02705 (2018); https://arxiv.org/abs/1811.02705.
Davide Pierangeli is a postdoctoral scientist, Giulia Marcucci is a PhD scientist, and Claudio Conti is a professor, all at the University of Rome La Sapienza and Institute for Complex Systems CNR, Rome, Italy; e-mail: [email protected]; www.uniroma1.it/it.