In the 1950s, researchers discovered that light could propagate along the surface of a metal placed next to a dielectric material. This type of electromagnetic surface wave—surface plasmon polariton (SPP)—is a quasiparticle formed by the interaction of electrons and photons. In physics, the term plasmon is a short form of quantum of plasma oscillation and refers to the coherent oscillation of electrons in the metal. Polariton, on the other hand, refers to the electromagnetic wave, or photons, which this electron oscillation couples with.
SPPs offer a way to compress light. The wavelength of a polariton wave is shorter than that of an electromagnetic wave propagating in free space. Because of this shorter wavelength, plasmon technology (plasmonics) has the potential to manipulate light at the nanoscale, one of the draws of SPPs.
While SPPs are well suited for applications such as biosensors, optical switching, and surface-controlled electrochemical reactions, plasmonic devices operating at telecommunication and optical frequencies face significant challenges due to the losses experienced in the plasmonic materials. SPPs can readily be modeled and simulated with numerical methods used for solving Maxwell’s equations. For example, the well-known finite element method can be used to gain a deeper understanding of plasmonic structures.
Modes of propagation
In free space, an unguided electromagnetic wave typically propagates as a transverse electromagnetic (TEM) wave. This is a mode of propagation where the electric and magnetic field components are restricted to directions perpendicular, or transverse, to the direction of propagation.
One of the characteristics of TEM waves is that light waves of all wavelengths travel at the same speed; therefore, the wave is nondispersive. In a waveguide, however, the constraints imposed by its boundaries often mean the mode of propagation is different than TEM. Similarly, for a SPP wave, the mode of propagation is transverse magnetic (TM) rather than TEM. The magnetic field components of a TM wave only exist perpendicularly to the direction of propagation, whereas the electric field components exist in both the direction of propagation and the transverse plane. Consequently, with this mode of propagation, light waves of different wavelengths will travel at different speeds. This phenomenon—called dispersion—breaks up white light into rainbow colors. Light waves of different wavelengths travel at different speeds through the prism and exit it at different times. One of the uses of optics simulation software is to understand dispersion relationships in various optical media, including guided waves such as polariton waves.
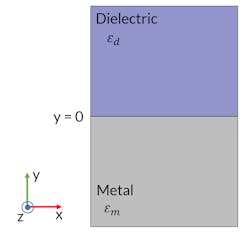
Polariton waves along a silver-air interface
A surface polariton wave travels parallel to the metal-dielectric interface, and the field strength decreases rapidly in the direction perpendicular to it. Several types of material configurations can support this type of wave, the simplest being a bulk metal-dielectric interface (see Fig. 1). Consider this configuration in a 3D coordinate system where the material interface is in a plane at y = 0. The region where the dielectric is present is y > 0, and the metal region is y < 0.
The exponential decay in the direction perpendicular to the surface directs the electromagnetic energy in the direction along the interface, which is what allows the wave to propagate. By matching the mathematical expressions for the wave on either side of the material interface, we can show that exponential decay in the y direction can only happen if the real part of the complex-valued electric permittivity has a different sign on either side of the interface. This happens if one of the materials is a metal (negative permittivity) and the other is a dielectric material (positive permittivity).
When analyzing the polariton wave, several important wavelengths are involved. First, the free-space wavelength, λ0, of the light being fed into the system where we excite the polariton wave. Second is the propagating wavelength, λprop, which, in this example, is in the x direction. A propagating TM wave will make this wavelength shorter than the free-space wavelength. This is a dispersive property of the wave, and it corresponds to compressing light.
In the computational results shown in Figures 2 and 3, the metal is silver and the dielectric material is air. It is also important to note that the wave propagates from left to right. These and the other simulations cited were created using COMSOL Multiphysics and its wave optics add-on module.
Be careful when exciting the structure since the free-space and propagating wavelengths are different—shining light directly at the material interface and hoping the polariton wave will start propagating is not effective, because the wave will just be reflected. Mathematically speaking, the reciprocal of the wavelength (known as the wave vector) must match the surrounding dielectric material that the wave is coming from—in this case, air—as well as the air-silver configuration. To ensure matching wave vectors in the models shown here, the software’s port boundary condition feature was used. In a practical setup, we could, for example, carefully position a prism to achieve a match.
Dispersion and Q factors
For a polariton wave, the propagation wavelength is always shorter than the free-space wavelength used to feed the system. We get light compression due to dispersion for shorter wavelengths. This can be visualized by plotting the free space vs. the propagating wavelength, as shown in Figure 4. For comparison, the free-space light dispersion curve, which has no dispersion, is plotted and a straight line called the light line.
The study of SPP waves typically involves defining the Q factor, a quantity representing the ratio of the real and imaginary parts of the propagation wave vector. Polariton waves with a larger Q factor, or a relatively smaller imaginary part, can propagate for a longer distance relative to their wavelength before they decay. For practical applications such as optical switches and biosensors, a larger Q factor is usually required.
A Q factor can be plotted as the coloring of a dispersion curve. This can be seen in Figures 4 and 5, where a brighter color represents the higher Q factor, and the lower Q factor is in a darker color. For comparison, an analytical expression for the dispersion and Q factor is plotted as a solid curve.
While simulating SPP waves in a metal-dielectric interface is a useful introduction to polariton wave propagation and dispersion, a more compelling scenario is that of a thin metal film overlayed by dielectric layers. In this case, the coupling between the top and bottom surfaces’ polariton waves creates symmetric and antisymmetric modes reminiscent of coupled mechanical harmonic oscillators. By modeling a 12-nm-thick aluminum film surrounded by dielectric layers that are 4 nm thick and have a refractive index of 2, we can identify two SPP mode branches (see Fig. 5). The symmetric mode has a greater Q factor and corresponds to the upper branch, whereas the lower branch corresponds to the antisymmetric mode with a smaller Q factor.
SPPs in graphene
As the electronics and optoelectronics industry shifts toward miniaturization, 2D materials such as graphene are becoming increasingly popular. Graphene supports SPPs in the infrared (IR) regime and can be advantageous for metamaterials and harvesting IR radiation. The conductivity of graphene can be tuned by changing its Fermi energy via electric tuning or chemical doping, making SPPs tunable, which is not easily achievable in metals.
Graphene’s SPP dispersion curves differ based on their conductivity, with a steep light line due to graphene having a much larger SPP wave vector than the free-space photon wave vector. In graphene, the SPP wavelength is smaller, achieving significant wavelength compression. Still, the Q factor is low, which can be improved by refining the graphene’s crystalline quality or cooling it down. In the graphene dispersion curves shown in Figure 6, the frequency is plotted against the magnitude of the propagation wave vector. The absence of a SPP in the dispersion plots around 33 THz (the empty horizontal band) may appear unusual, but the absence occurs because the substrate material, SiO2, has a negative permittivity owing to its phonon resonance.
The scientific community is making extensive efforts to discover plasmonic devices and designs with commercial potential. Optical simulation software has become indispensable in the design and development of plasmonic devices, because it enables virtual experimentation with various designs and materials, optimizes performance, and provides insight into physical mechanisms at play. Through simulation software, researchers can accelerate the exploration of new plasmonic designs, improve existing designs, and enhance their fundamental understanding of plasmonic devices.