Quantum Photonics Research: Birth and death of time crystals predicted for quantum computing
In May 2018, Aalto University (Espoo, Finland) researchers said they had demonstrated the existence of quantum time crystals in May 2018, defined in simple terms as structures that do not repeat in space (like snowflakes), but repeat in time—offering long-term coherence that could be useful for quantum computing operations.1 Time crystals were first proposed by Nobel Laureate Frank Wilczek in 2012.
Adding to this emerging research field, professor C. H. Wu from the Missouri University of Science and Technology (Rolla, MO) has now proved a special type of quantum computing, executed by an array of entangled atoms under periodic external perturbation (from periodic laser pulsing), that allows these time crystals to exist in the form of periodic space-time blocks.2
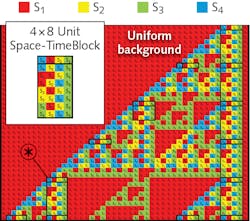
The signature of these time crystals from an array of N entangled atoms is a periodic space-time block of the sizes between N × 2N and N × 4N, independent of the period of the external perturbation. Such a periodic space-time block is the quantum computing result, performed by the N entangled atoms. Here, each atom is manifest as a quantum processor and the N-atom chain forms a parallel quantum computing machine in the cellular automata architecture.3
Space-time blocks
All parallel computing performs spatial transformations and there are billions of varieties. For general-purpose parallel computing, one must start with an addition operation of two bit-strings with four states.
A space-time block obtained from such an addition operation is just a simple finite rectangular block wherein the last row of the computational state contains the addition result. There are 16 cellular automata transition rules associated with any addition operation and it is performed on a Euclidean chain—the most singular situation. The quantum processor needed to perform those 16 rules is a man-made quantum network (U.S. Patent #8,525,544). If this quantum processor is wired differently, then the chain becomes helical and biological birth-and-death of a different type of space-time block is produced.
The size of the space-time blocks is always N × N, in the form of square helical time crystals. This applies to DNA, for example, with its four CGTA “computational states.” The 16 cellular automata rules for birth-and-death of space-time blocks are different from those used in the addition rules, even though the same quantum processor is used in both cases.
For the space-time crystals proposed by Frank Wilczek and the subsequent experimental verifications, Wu says that the explanations published so far are quite awkward, because the Hamiltonian is a “sum” of several terms. That means “addition rules” in cellular automata must be used because the Hamiltonian is in “additive” form.
An entanglement theory
In Wu’s formulation, the components of the Hamiltonian of atoms and those of the entanglements are automatically built in. When a man-made quantum processor is replaced by a four-state free-electron atom, the four orthogonal states are linked to the four computational states through a proper unitary transformation that is well known in textbooks.
When an orthogonal vector is transported from one cell to act on its neighboring state, a proper “phase counting” or “a quantum computation” has occurred. It also means in cellular automata of parallel computing, an orthogonal state is simultaneously an operator and a state at the same time, depending on its location. Those requirements are reflected back to the computational state as the observable of the quantum computing process. Wu then shows the computational states must be cyclic and with an equal probability of transitions (see figure). Note that additional rules do not have an equal probability.
Time crystals are simply manifestations of the fact that the computational states can exhibit the inner quantum mechanical operations of any entangled atoms as an observable. When the entanglement is in a large system, birth and death of identical time crystals can be reproduced at a different location of the chain. Essentially, this birth-and-death process provides the foundation for true artificial intelligence and quantum teleportation applications.
REFERENCES
1. S. Autti et al., Phys. Rev. Lett., 120, 21, 215301 (May 25, 2018).
2. C. H. Wu, Int. J. Eng. Sci. Invention, 8, 5, 1–6 (May 2019).
3. See http://bit.ly/TimeCrystalsRef.
About the Author

Gail Overton
Senior Editor (2004-2020)
Gail has more than 30 years of engineering, marketing, product management, and editorial experience in the photonics and optical communications industry. Before joining the staff at Laser Focus World in 2004, she held many product management and product marketing roles in the fiber-optics industry, most notably at Hughes (El Segundo, CA), GTE Labs (Waltham, MA), Corning (Corning, NY), Photon Kinetics (Beaverton, OR), and Newport Corporation (Irvine, CA). During her marketing career, Gail published articles in WDM Solutions and Sensors magazine and traveled internationally to conduct product and sales training. Gail received her BS degree in physics, with an emphasis in optics, from San Diego State University in San Diego, CA in May 1986.