Image Fusion: Spatial-domain filtering techniques dictate low-light visible and IR image-fusion performance
Image fusion is the art of combining multiple images from different sensors to enhance the overall information content as compared to the limited data found in a single-sensor image. For visible and infrared (IR) images, the difference lies in the fact that visible images are the result of reflected light while IR images result from the emission of radiation from the object being viewed. That is, visible images can be seen by the naked eye whereas IR images reveal concealed features. The fused visible-IR image provides supplementary information that improves the perception of the object for the viewer.
Categories of domain-based image fusion include transform domain, spatial domain, and a combination of the two called hybrid domain image fusion. In every category, image fusion involves the decomposition of the source images through some appropriate technique. This process is also termed multiscale decomposition, wherein the low- and high-frequency information present within the source images are separated. This information is then processed separately and fused to get a high-quality image.
The transform domain-based method uses certain transforms, including wavelet, discrete cosine, curvelet, and shearlet transforms, to achieve the task of multiscale decomposition. An averaging filter constitutes a window that is used to calculate the mean of the intensities of the pixels; afterwards, the value of the pixel under consideration (center of the window) is replaced with the calculated mean value. This filter can be used to remove small traces of high-frequency noise present in the 2D signal under consideration.
In the spatial domain, filters are used to achieve the task of decomposition through iterative smoothing. Layers of information are extracted (low-frequency or base layer, and high-frequency or detail layer) with the help of conventional filters, including mean, median, average, bilateral, and Gaussian, for example. These layers are then modified and fused to maximize the transfer of information from the source images to the fused image. The modifications lead to the efficient extraction of various features of an image that are used to enhance the performance of overall image fusion algorithms that in turn modify spatial information such as pixel intensity, mean, root-mean-square values, and standard deviation to quantify the performance of the overall fusion algorithm.
In our image-processing experiments, we have tested and compared various spatial domain filters for fusion of images captured under low-light conditions. In addition to being very noisy, these images also have very limited perceptibility, as they lack detail due to poor illumination of objects in the scene. That is, the images captured using visible-light sensors may lack some high-frequency details of the objects, but the images captured using IR sensors can provide that data as complimentary information. The fusion of information gathered from these two sensors solves the low-light problem and has found myriad uses in civil and military surveillance, concealed weapons detection, and analysis of geographical landscapes over time.
Filtering basics
All spatial-domain filters discussed in this section are used to decompose the visible and IR source images into a base layer and a detail layer. The base layer contains large-scale variations in intensity, while the detail layer captures small-scale intensity variations within the image. These filters have evolved over time in the following order: average, median, Gaussian, bilateral, cross/joint bilateral, and guided.
The average filter is the simplest and is implemented using a simple low-pass finite impulse response (FIR) filter. As the name indicates, it replaces the pixel value under consideration with the average of the pixel intensities considered over a particular window of a particular size.1
Defined as a nonlinear edge-aware filter, the median filter aims to provide the best possible representative to the pixel under consideration by considering its surrounding pixels according to the window size of the filter. This filter replaces the pixel under consideration by the median values of the pixels in that window—consequently, no pixel value is changed in the filtering process, facilitating its edge-preserving abilities.2
A simple spatial filter with a Gaussian kernel is termed a Gaussian filter. It is the most basic filter with a Gaussian function as its impulse response. Specifically, a 2D Gaussian kernel is used to achieve a “blur” operation and results in images with a unique smoothing behavior, depending on the standard deviation of the pixel intensities in the image.3
The nonlinear bilateral filter is used to overcome the drawbacks of the Gaussian filter in that it preserves edge information by preventing the averaging operation on the edges while smoothing the low-frequency areas by performing an averaging operation. The two factors that are taken into consideration for designing the bilateral filter are the weighted spatial (Euclidean) distance and the photometric distance between the pixels, hence providing a local adaptability to the changes in the signal or an image in this case.4
The main drawback of the nonlocal cross/joint bilateral filter approaches is that they perform over-smoothing of the edge information. This avoids further processing of the image, whether it is a de-noising or image-fusion or image-enhancement procedure. Basically, this filter is used to synthesize a high-quality image from multiple low-quality images.5, 6
Finally, the guided filter was proposed to deal with the drawbacks of the bilateral filter. Not only is the bilateral filter known to introduce gradient-reversal artefacts, but it is also computationally complex. For the guided filter option, a guidance image is used to build the filter kernel. The output of the filter also depends on the guidance image and on its linear transform.7
Image fusion methodology and experiments
From visible and IR images of a scene captured in low-light conditions, we used various spatial filters to decompose the two source images and then fused them together using a maximum fusion rule in which the pixel having more intensity is chosen for the final fused image.
Using a common image dataset and Matlab R2015b software, grayscale images measuring 512 × 512 pixels are fused and compared.8 The first step is to decompose the source images using one of the spatial filters discussed previously to obtain a smooth version of the input source image (see Fig. 1).
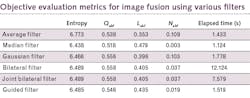
From this smooth version, which is free of noise and lacking significant edge information, a detailed image is obtained by subtracting the filter output from the original image. This detail image consists of all the relevant edge information and lacks the common low-frequency information. These layers, which are obtained from the filtering operation, can be enhanced to improve the overall fusion performance both objectively and subjectively.The experiments show that loss of information is quite high for average-filter-based image fusion, although entropy is highest in this case. Also, in terms of the time taken to implement the process of fusion for each algorithm, the median-filter-based fusion method performs the best.
By analyzing a real-time application of image-fusion algorithms in low-light conditions, the visible image does not clearly reveal the presence of a human form. However, the IR image clearly displays the outline and presence of the human body, although the characteristic details are missing. Image fusion helps to merge these two datasets for improved target detection and recognition.
In general, spatial-domain filtering is very useful in understanding the dynamics of an efficient image fusion algorithm. In general, the joint bilateral filter outperforms all other filters in terms of objective metrics as well as visual inspection. This observation, however, is subjective in that the success of the various filtering methods depends on the image dataset presented; different images can be fused with different degrees of success, depending on what objects need to be extracted from a particular scene.
REFERENCES
1. D. P. Bavirisetti and R. Dhuli, Infrared Phys. Technol., 76, 52–64 (May 2016).
2. A. Hameed and H. Mohammed, Int. J. Comput. Appl., 178, 2, 22–27 (Nov. 2017).
3. B. S. Kumar, Signal Image Video P., 6, 7, 1159–1172 (2013).
4. L. Caraffa, J. Tarel, and P. Charbonnier, IEEE Trans. Image Process., 24, 4, 1199–1208 (Apr. 2015).
5. Z. Farbman et al., ACM Trans. Graph., 27, 67 (2008).
6. B. K. Shreyamsha Kumar, Signal Image Video P., 9, 5, 1193–1204 (Jul. 2015).
7. K. He and J. Sun, “Fast guided filter,” arXiv:1505.00996 [cs] (May 2015).
8. See http://bit.ly/imageprocessing8.
9. C. S. Xydeas and V. Petrovic´, Electron. Lett., 36, 4, 308 (2000).
About the Author
Ayush Dogra
Assistant Professor - Senior Grade, Chitkara University Institute of Engineering and Technology
Dr. Ayush Dogra is an assistant professor (research) - senior grade at Chitkara University Institute of Engineering and Technology (Chitkara University; Punjab, India).
Apoorav Maulik Sharma
Research Fellow, Department of Electronics & Communication Engineering (ECE)
Apoorav Maulik Sharma is a research fellow in the Department of Electronics & Communication Engineering (ECE) in the University Institute of Engineering & Technology (UIET) at Panjab University (Chandigarh, India).
Bhawna Goyal
Assistant Professor, UCRD and ECE departments at Chandigarh University
Dr. Bhawna Goyal is an assistant professor in the UCRD and ECE department at Chandigarh University (Punjab, India), and in the Faculty of Engineering at Sohar University (Sohar, Oman).
Sunil Agrawal
Professor and Coordinator, Department of Electronics & Communication Engineering (ECE)
Sunil Agrawal is professor and coordinator in the Department of Electronics & Communication Engineering (ECE) in the University Institute of Engineering & Technology (UIET) at Panjab University (Chandigarh, India).
Renu Vig
Professor, Department of Electronics & Communication Engineering (ECE)
Renu Vig is a professor in the Department of Electronics & Communication Engineering (ECE) in the University Institute of Engineering & Technology (UIET) at Panjab University (Chandigarh, India).