Ultrafast Lasers: Numerical simulation aids design of fiber-based ultrafast laser sources
Optical fibers are widely used in laser technology. In the area of ultrafast lasers, optical fibers as gain media have some advantageous properties, such as a large gain in combination with a large gain bandwidth. On the other hand, both nonlinear and dispersive effects are far stronger in optical fibers compared with bulk laser crystals and glasses.
Strong nonlinear effects often set limits for achievable performance. The physical details can be quite involved, and this has consequences for the design process—performance potentials can usually be realized only based on a comprehensive quantitative understanding. Note that even for continuous-wave (CW) devices, the operation of fiber lasers and amplifiers is more difficult to understand and analyze than that of bulk devices. For example, this happens because of strong saturation effects, high gains, amplified spontaneous emission, and the quasi-three-level nature of most fiber gain media.
Mode-locked fiber lasers
Although one can in principle start with very low-energy pulses and then apply a lot of gain from a fiber amplifier, it is usually advantageous to start with seed pulses of higher energy. This is essentially because a very high required amplifier gain enforces the use of multiple amplifier stages and some intermediate devices like filters, isolators, or modulators, making the system more complex. In addition, noise issues may become more severe.
Another aspect is that the average intracavity power in any laser should be several times the gain-saturation power to operate a few times above the laser threshold. That, in combination with a typical pulse repetition rate and pulse duration, leads one into a regime with substantial peak power and thus substantial nonlinear effects.
Traditional concepts like soliton mode-locking are thus hardly usable, as soliton pulse energies are usually quite low. Modern mode-locked fiber lasers are often based on more-sophisticated operation principles. All-normal-dispersion laser resonators are often used, in which strongly up-chirped pulses circulate. The intracavity pulse duration is substantially increased in conjunction with the strong chirp. The substantial optical bandwidth allows one to obtain very short pulses using a dispersive compressor outside the laser resonator. The significant increase of pulse bandwidth because of self-phase modulation is compensated in every resonator round trip by an intracavity bandpass filter. This technique was pioneered by Frank Wise and his research group at Cornell University (Ithaca, NY).
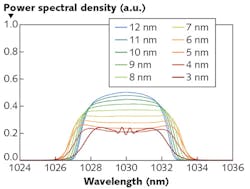
For example, we consider a fiber ring laser, which essentially comprises an output coupler, a bandpass filter, a passive fiber, a ytterbium (Yb)-doped fiber, a Faraday isolator, and a saturable absorber. When we gradually reduce the filter bandwidth, the spectrum of the steady-state output pulses first becomes more and more flat in the middle. Reducing the bandwidth further, we obtain maxima near the edges (see Fig. 1).
Curiously, the output bandwidth increases if the filter bandwidth is decreased, essentially because initially narrowband pulses exhibit less temporal broadening in the fiber and thus reach a higher peak power later. However, instability results if we go too far—for the lowest filter bandwidth in our example, the laser is close to that stability limit and the pulse energy is decreased because of the losses at the intracavity filter. Raising the pump power has an effect similar to decreasing the filter bandwidth, except that of course it increases the pulse energy.
The performance limits resulting from the mentioned instability, which depend on various design details (for example, on the parameters of the saturable absorber), cannot be properly explored without acquiring a comprehensive quantitative understanding of the operation. Numerical simulations are the only practical method for creating that understanding. They allow one to look into the device to, for example, explore the temporal and spectral evolution of the pulses within the fibers. Before purchasing and assembling the required optical components, one can answer important questions—for instance, how much saturable absorption is required and what dispersion map is suitable.
High-repetition-rate amplifiers
It may seem easy to strongly amplify ultrashort pulses in an active fiber, providing high gain with a substantial gain bandwidth. However, fiber nonlinearity in particular is a limiting factor.
The technical challenges depend very much on the operation regime. We first consider ultrafast sources with a high pulse repetition rate of tens or hundreds of megahertz. Here, one directly amplifies the output of a mode-locked laser (which may itself be a fiber laser or in some cases a gain-switched laser diode), which can also be used to produce picosecond seed pulses.
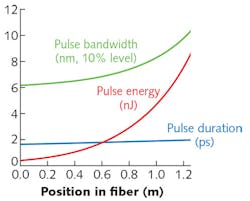
As an example, we take the output pulses of the previously discussed fiber laser and amplify them further in a 1.25-m-long, Yb-doped single-mode fiber with 5 µm core radius, backward-pumped with 800 mW at 975 nm. Figure 2 shows that we can substantially increase the pulse energy and at the same time obtain a significantly increased pulse bandwidth because of self-phase modulation, while the pulse duration increases only slightly. A dispersive compressor after the amplifier can reduce the pulse duration from approximately 2 ps to 290 fs. In fact, because of their increased bandwidth, the obtained pulses are substantially shorter than those possible via direct compression of the laser pulses (517 fs).High-pulse-energy amplifiers
For obtaining substantially higher pulse energies, one typically reduces the pulse repetition rate with a pulse picker, which transmits only every nth laser pulse. A lower repetition rate of, for example, 100 kHz allows for substantial pulse energies without excessive average powers. However, we then need to deal with two additional challenges.
First, the required amplifier gain will be correspondingly higher, which can lead to problems with strong amplified spontaneous emission (ASE). This often forces one to use additional amplifier stages and means to suppress ASE between them—for example, bandpass filters or optical switches in addition to Faraday isolators to suppress backward-propagating light.
And second, the increased peak powers further increase the strength of nonlinear effects well into the regime where, for example, stimulated Raman scattering becomes detrimental. A hard limit is set by nonlinear self-focusing at peak power levels of several megawatts.
The challenge arising from the fiber nonlinearity often forces one to apply the method of chirped pulse amplification (CPA). One first needs to dispersively stretch the pulses to durations of, for example, hundreds of picoseconds or even a few nanoseconds to limit the peak power in the following amplifier stage(s). Subsequent dispersive compression then becomes substantially more challenging since one requires a compressor that can deal with a wide range of group delays within the pulse. Chirped volume Bragg gratings (VBGs) can be a compact solution, but for the longest stretched pulse durations, one requires bulk diffraction gratings, which consume far more space and involve sensitive alignment.
The need for numerical simulations becomes even stronger for CPA devices. For example, simulations can be used for checking the match of the chromatic dispersions of stretcher and compressor, also taking into account nonlinear phase changes in the amplifier fiber. In addition, other aspects such as ASE need to be checked carefully. Quite obviously, a trial-and-error approach is not suitable for such design tasks, particularly when high performance is required.
About the Author
Dr. Rüdiger Paschotta
Founder and Managing Director, RP Photonics Consulting
Dr. Rüdiger Paschotta has done a Ph.D. and a habilitation in physics. He is author or coauthor of more than 100 articles in scientific journals, and of several books and book chapters. His best known publication is the online Encyclopedia of Laser Physics and Technology. He is also well known as a course instructor at conferences.
In 2004, he founded the company RP Photonics Consulting, offering technical consultancy, staff training courses, and simulation and design software for fiber optics, lasers, ultrashort pulse generation, and multilayer optics.