Interferometry: Radial shearing interferometer algorithm handles square apertures

Standard wavefront-measuring interferometers operate by combining the wavefront under test with an unaberrated reference beam; the two beams interfere, producing fringes that provide information on the shape of the test wavefront (the Fizeau interferometer is the most common configuration, due to its simplicity). While the sensitivity of this method is very high, it has one problem: because of the fact that a reference beam is required, such an interferometer cannot be simply placed somewhere into an optical beam to measure the wavefront at that point.

Interferometric and noninterferometric methods exist that do allow measurement of a wavefront without the requirement for a reference beam. A noninterferometric approach is the well-known Shack-Hartmann wavefront sensor (SHWFS) used in adaptive optics. Unlike interferometric approaches, however, a SHWFS samples a wavefront only at a relatively low number of discrete points.

One form of interferometer that can directly accept a test wavefront with no reference wavefront is the shearing interferometer: here, the test wavefront is interfered with a positionally shifted duplicate of itself—either translationally (lateral shear) or by changing the size of the duplicate (radial shear).

A group of laser-fusion researchers at Sichuan University (Chengdu, China) and the Research Center of Laser Fusion at the China Academy of Engineering Physics (Mianyang, China) want to use a so-called cyclic radial shearing interferometer (CRSI) to spot-check the beam wavefront in their laser system, and have developed a wavefront-reconstruction algorithm for the interferometer that is based on Legendre polynomials.¹ The system allows diagnosis of transient pulses with high speed and accuracy.

Legendre polynomials for square aperture

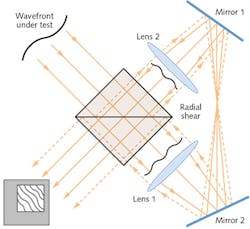
In a CRSI, light cycles in both directions through the interferometer because of a triangular light path (see figure); radial shear is provided by an asymmetric arrangement of focusing lenses (actually, a Keplerian telescope). Lateral shear can also exist. A software algorithm is used to reconstruct the wavefront.

Because many laser-fusion system apertures are rectangular rather than circular, the Chinese researchers chose to use Legendre polynomials rather than other types, as the x- and y-based Legendre polynomials are orthogonal with respect to a rectangle while, for example, radial Zernike polynomials aren’t. Certain low-order terms of the orthonormal Legendre polynomials are directly related to common aberrations such as piston, x and y tilt, x and y defocus, x and y primary coma, and so on. The researchers aim was to test their new algorithm against an older iterative nonpolynomial algorithm that, although accurate, was slow.

To numerically test their algorithm, the researchers generated an arbitrary wavefront consisting of six orders (28 terms) of Legendre polynomials with random coefficients; the modeled CRSI had both radial and lateral (in both x and y) shear. The peak-to-valley residual error between the generated and reconstructed wavefront was very small—on the order of 10–14 nm.

The researchers then experimentally tested the algorithm on a real CRSI, slightly tilting its beamsplitting cube to create a carrier frequency fringe pattern. A crosshair was inserted at the input plane of the CRSI and was imaged, along with the fringes, onto a CCD camera. The lateral shear added was about 15 pixels in y and -1 pixel in x. The interferogram of a 4-mm-thick piece of standard window glass was taken, and the interferogram without the window glass subtracted from it to eliminate system error. The new algorithm reconstructed the wavefront similarly to that of the older, accurate-but-slow algorithm.

For the future, the group plans to increase the number of polynomial terms as much as possible (although this increases noise), while using as small a shear as they can (which reduces noise).

REFERENCE

1. E. Kewei et al., Opt. Express (2015); doi:10.1364/OE.23.020267.