Adaptive Optics: Laser beam control takes advantage of advanced wavefront sensing
MICHAEL J. STEINBOCK, JASON D. SCHMIDT, and MILO W. HYDE IV
On any given night, people can see the distorting effects of atmospheric turbulence in the twinkling of the stars. With that said, adaptive optics (AO) systems can remove this twinkling in real time. These AO systems typically feature a wavefront sensor (WFS) and deformable mirror (DM) configured in a feedback-control loop. The WFS measures the phase, and the surface of the DM is adjusted so that the wavefront is flattened upon reflection. This greatly improves astronomers' views of the universe and the scientific research that can be accomplished with those sharper, brighter images. The first real-time AO system for compensating a bright star was demonstrated at the Air Force Maui Optical Site on a 1.6 m telescope in 1982.
Branch points pose a challenge
By today's standards, compensating a bright star overhead is an easy problem to solve. New problems, like compensating wide fields of view, dim objects, and very strong turbulence present novel challenges for researchers. When the object is almost directly overhead, the light merely accumulates phase delays at the very end of its propagation path in the dense, turbulent ground layer. In contrast, when the path becomes more horizontal, significant phase aberrations are accumulated throughout the path. As the light propagates further, different parts of the beam converge and diverge, leading to bright and dark spots across the beam.
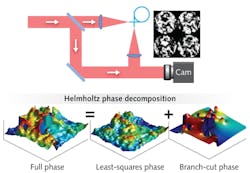
This spatial self-interference is called scintillation, and it arises in many applications of laser beam projection, like actively illuminated imaging, free-space optical communication, and laser weapons. Figure 1 shows a diagram of an AO system for beam projection including a fast-steering mirror (FSM), deformable mirror (DM), wavefront sensor (WFS), tracking/imaging camera, controllers, and drivers.
In 1992, David Fried and Jeffrey Vaughn at the Optical Sciences Company (Anaheim, CA) described so-called branch points and branch cuts that appear in the phase when the scintillation is strong enough.1 Branch points are points within the entrance pupil where the light wave amplitude is zero and the phase is undefined. Circulating about any branch point is a characteristic rotational phase. Since rotational fields are nonconservative, a sharp 2π cut must be arbitrarily placed within the rotation in order to be conjugated by a DM. The right side of Figure 1 shows a hypothetical branch point and the surrounding rotational phase, along with an associated branch cut.
In 1998, Fried presented many of the difficulties that AO faces due to branch-point effects.2 Of great importance is the reconstruction of measured wavefront gradients into a smooth wavefront surface to apply to the DM for correction. Fried showed that traditional least-squares reconstruction is unable to reconstruct the rotational wavefronts associated with branch points. Without the ability to reconstruct the branch-point wavefront contributions, AO correction is likewise greatly limited.
Since then, more advanced algorithms for reconstructing the branch-cut portion of the wavefront have been developed. Yet even with advanced algorithms, researchers have found that AO systems based around the traditional Shack-Hartmann WFS do not perform well in strong scintillation.3 Further work was needed.
A new sensor to handle branch points
In the early 2000s, Jeffrey Barchers and Troy Rhoadarmer at the U.S. Air Force Research Laboratory's (AFRL's) Starfire Optical Range (Kirtland Air Force Base; Albuquerque, NM) adapted the widely known point diffraction interferometer into an instrument called a self-referencing interferometer (SRI), as shown in Figure 2.In an SRI, the received light is split along two paths, one of which couples into a single-mode fiber to spatially filter the beam. When light from the two paths is recombined, an interference pattern is formed. Typically, the light that traverses the fiber leg of the SRI is further split so that four interferograms are made. A common approach is depicted in Figure 2, where four interferograms, formed from phase delays of 0, π/2, π, and 3π/2, are shown. In this way, the phase surface φ can be estimated using a standard four-bin phase-shifting algorithm given by
φ = tan-1 (I1 – I3, I4 – I2), (1)
where I1, I2, I3, and I4 are the interferograms at phase shifts 0, π/2, π, and 3π/2, respectively, and a four-quadrant inverse tangent operator is used.4
The SRI provides a near-direct measurement of the phase wrapped within a 2π interval. Two AO design paths can be taken from here. A segmented DM can be quite successfully controlled from the wrapped outputs using an exponential controller. However, segmented DMs are considered unsuitable for high-power applications because of absorption at the intersegment gaps and diffraction off of the sharp segment edges. Continuous face-sheet DMs are proven for high-power applications, but they have difficulty matching sharp features in the phase surface, such as branch cuts. Use with an SRI requires a reconstruction algorithm to eliminate the sharp unwrapping cuts and also minimize the impact of any branch cuts in the field.
Computing the phase difference between adjacent rows and columns provides an estimate of the wavefront slopes that can be reconstructed into an unwrapped least-squares wavefront. The Helmholtz decomposition theorem allows expressing the full phase as the sum of irrotational (least-squares) and rotational (branch points) components, as depicted at the bottom of Figure 2. The branch-point component can be recovered by subtracting the least-squares phase from the wrapped phase computed in Eq. (1). The full, reconstructed phase φR is finally written as:
φR=φLS+W{φBP}=φLS+W{φSRI–φLS}, (2)
where φLS is the irrotational, least-squares component; φBP is the rotational, branch-point component; and W is an operator that wraps its argument into the interval (-π, π]. This method is termed the least-squares principal value (LSPV) method. In some literature, it is also called the "postprocessing congruence operation" or colloquially, "least-squares plus branch-point" reconstruction.5 The unwrapped phase is the input provided to the AO system's integral controller.
In 2006, the U.S. Air Force Scientific Advisory Board issued a challenge to AFRL's Directed Energy directorate and its collaborators. The challenge was to devise an effective laser beam control method in "deep turbulence" conditions. Compensating branch points due to scintillation is one aspect of the challenge, and it began to gain more attention.
At the Air Force Institute of Technology (AFIT), Jason Schmidt and Todd Venema realized that if an offset value h was added to φBP inside the wrapping operator in Eq. (2), the branch cuts would move. Their new technique computed the unwrapped phase with h = 0, π/2, π, and 3π/2, much like in the four phase-shifted interferograms shown in Figure 2. From these four options, they selected the one with the shortest total intensity-weighted branch-cut length, which has a high correlation to the Strehl ratio.6
Subsequently, Schmidt's Master's student, C. Pellizzari, conducted an exhaustive study of 16 distinct adaptations of the LSPV+4 algorithm. In 2010, Pellizzari and Schmidt showed that their best method, based on a Golden Section Search to select the h value for each frame, used seven intensity-weighted cut-length calculations and almost completely avoided the frequent, short-duration decreases exhibited by the original LSPV method.7
In 2014, M. Steinbock et al. further refined the LSPV-based variants for robust performance in the presence of shot and readout noise, which was absent from Pellizzari's earlier proof-of-concept studies. Consideration was given to the data-flow pipeline, noise-induced branch-point effects, and coupling between the tracking system and higher-order system. A new LSPV+7 variant was published in 2014, finding average improvements of 120% relative to traditional least-squares-based AO in the strong turbulence scenarios tested.8
For all of its successes, the LSPV-based methods face skepticism about whether or not there will be branch points present in outdoor field tests of beam projection systems in deep turbulence. When the AO system can sense a laser cooperatively transmitted from the other end of the path (as in free-space optical communication), most agree that branch points will manifest. However, when the AO system must use its own laser to illuminate an uncooperative target, the reflected spot can be quite broad, at least initially.As shown in Figure 3, widely spaced points can travel through portions of the atmosphere that impart fluctuations with little correlation between the two points. This is known as atmospheric anisoplanatism. The scintillation patterns and branch-point locations can be so different that the information is effectively "washed out" and the WFS becomes ineffective. It remains for researchers to study this problem for specific applications with relevant target sizes, measured turbulence conditions, and AO system architectures to truly determine the extent of the anisoplanatism effect and devise new ways to compensate for turbulence when the techniques described here become ineffective.
Authors' note
The technical results and conclusions expressed in this article are those of the authors and do not necessarily reflect the official policy or position of the sponsors, U.S. Air Force, the U.S. Department of Defense, or the U.S. government.
References
1. D. L. Fried and J. L. Vaughn, "Branch cuts in the phase function," Appl. Opt. 31, 2865–2882 (1992).
2. D. L. Fried, "Branch point problem in adaptive optics," J. Opt. Soc. Am. A 15, 2759–2768 (1998).
3. J. D. Barchers et al., "Performance of wavefront sensors in strong scintillation," Proc. SPIE 4839, 217–227 (2003).
4. D. Malacara, M. Servín, and Z. Malacara, Interferogram Analysis for Optical Testing (CRC Press, 2010).
5. D. C. Ghiglia and M. D. Pritt, Two-Dimensional Phase Unwrapping: Theory, Algorithms, and Software (Wiley, 1998).
6. T. M. Venema and J. D. Schmidt, "Optical phase unwrapping in the presence of branch points," Opt. Express 16, 6985–6998 (2008).
7. C. J. Pellizzari and J. D. Schmidt, "Phase unwrapping in the presence of strong turbulence," in Proc. IEEE Aerospace Conf. (IEEE, 2010), pp. 1–10.
8. M. J. Steinbock, M. W. Hyde, and J. D. Schmidt, "LSPV+7, a branch-point-tolerant reconstructor for strong turbulence adaptive optics," Appl. Opt. 53, 3821–3831 (2014).
Michael J. Steinbock is a PhD student and Milo W. Hyde IV is an assistant professor at the Air Force Institute of Technology, WPAFB, OH; email: [email protected]. Jason D. Schmidt is a senior scientist at MZA Associates Corp., Dayton, OH; www.mza.com.