PHOTONIC FRONTIERS: OPTICAL SINGULARITIES: Optical singularities range from black holes to laser speckle and rainbows
In mathematics, a singularity occurs when some quantity is not definable, not differentiable, or otherwise behaving badly. For example, a graph of y=1/x has a singularity at x=0 because dividing by zero yields an infinite result. The best-known physical singularity is the center of a non-rotating black hole, where theory predicts that the curvature of space becomes infinite.
Optics has its own singularities that occur where optical field quantities such as phase and polarization parameters cannot be defined. Those singularities are "a matter of semantics, not a region where Maxwell's equations don't behave," says Grover Swartzlander of the Rochester Institute of Technology (Rochester, NY). Destructive interference of two waves leaves a region where light has no amplitude, and therefore no definable phase—an optical singularity called an optical vortex because light swirls around the dark zone. Constructive interference of reflected or refracted light can produce bright lines called caustics, where in theory the amplitude is infinite, and the phase thus also indeterminate and singular. Polarization singularities also are possible.
Now developers are trying to tame optical singularities. Optical vortices offer ways to increase fiber-optic transmission capacity or to spot planets orbiting other stars. Optics also can simulate the physics of black holes, which could lead to more efficient light trapping in integrated photonic devices, says Ulf Leonhardt of the Weizmann Institute of Science (Rehovot, Israel)
Wave effects and singularities
Studies of peculiar wave effects in the nineteenth century laid the groundwork for optical singularities.
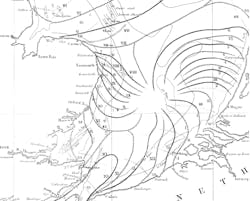
In the 1830s, William Whewell plotted lines in the North Sea to identify where tides were high at a particular time in the tidal cycle. He found that the lines of common tidal height revolved around a central point in the sea where there was no tide (see Fig. 1).1 "What Whewell discovered were the phase singularities of the tide waves...now recognized as important features of all waves," wrote Michael Berry of the University of Bristol (Bristol, England) in a Nature retrospective.2 "In acoustics, the singularities are threads of silence; in light they are optical vortices."
Berry traced polarization singularities back to an 1832 discovery of optical axes in anisotropic crystals by William Rowan Hamilton. Those are the two singular zones where light with different polarizations has speeds that are identical, not different as in the rest of an anisotropic crystal.
Berry also cited George Biddell Airy's 1838 discovery that the existence of the second-order (double) rainbow meant the rainbow was a caustic, a line along which light rays are focused from a range of angles. Ray optics predict infinite brightness along caustics, but only for an infinitely small wavelength; in practice, wave optics blur the lines to make the intensity finite.
Optical vortices and singularities
Light waves that interfere destructively circulate around the zero-intensity region like air around the center of a hurricane, says Swartzlander. As in the North Sea tides, the circulation pattern looks like a vortex, and gives the light an optical angular momentum. Properly speaking, the light contains an optical vortex if the gradient of its phase is a vector pointing either clockwise or counterclockwise along a closed path. This optical angular momentum can be transferred to particles illuminated by the light, so it can spin particles trapped by optical tweezers.
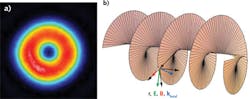
The donut mode of a laser looks like a ring of light with a central dark spot, but it actually is an optical vortex. The light waves circle the dark center in a screw-thread pattern (see Fig. 2). The waves interfere constructively in the bright outer zone, and destructively in the inner dark area, forming the central vortex where the amplitude is zero and the phase is thus undefined. Vortex beams also can be produced by passing light through a suitable computer generated hologram or spatial light modulator (see Fig. 2b).Light can produce vortices everywhere, but our eyes average over time and wavelength so we miss most of them. One example is laser speckle. "Each one of the dark nodes between the light speckles is an optical vortex, where the light waves are crossing and interfering," says Swartzlander.
Vortices can be given different amounts of angular momentum by passing the light through different masks, creating distinct modes that could be used for modal-division multiplexing in high-capacity optical communications. The idea has attracted considerable attention. In June 2012, Alan Wilner's group at the University of Southern California combined vortex modal division multiplexing with polarization multiplexing to transmit 1.37 Tbit/s through free space with an impressive spectral efficiency of 25.6 bit/s/Hz.3
The USC experiment sent light only a meter through air in the laboratory, but its success was an important milestone. Adaptive optics could be used to overcome air turbulence to allow longer free-space links. Signals also could be transmitted through multimode optical fibers, but not the singlemode fibers used in most existing networks. The USC group suggests trying novel multimode fibers containing annular rings with high refractive index.
An optical vortex also can be used as a coronagraph, which blocks light from a central star to look for faint nearby objects.4 By coupling one to an astronomical telescope, Swartzlander reduced the light received from the primary star in a resolvable binary pair by 97%. In 2010, a group at the Jet Propulsion Laboratory (Pasadena, CA) imaged three exoplanets orbiting one star using an optical vortex coronagraph with a 1.5 m telescope.5 The coronagraph is now used on the 200-inch Hale Telescope at Palomar Observatory (San Diego County, CA).
Polarization singularities also are being studied. Normally, polarization is measured as the angle of the major axis of a polarization ellipse. However, with circular polarization, the ellipse becomes a circle, so the major axis does not exist, and its direction cannot be measured—creating a singularity, although that can be regarded as a singularity in the material rather than in the light itself.
Optical black holes
Optical black holes are not true singularities. They use optical effects to simulate gravitational black holes, which are singularities. The distinction is important.Gravitational black holes have two key characteristics—a horizon some distance from the center which traps light, and a central singularity with density that may be infinite at the very center. Under suitable conditions, optics can simulate either the singularity or the event horizon, but not both simultaneously.
Massive objects distort space, as Sir Arthur Eddington famously demonstrated by measuring how stellar positions changed from their normal values when the Sun stood between the Earth and the stars during a 1919 solar eclipse. "Refractive index changes the measure of space for passing light in the same way that gravity modifies it for light. Consequently it is easy to understand a great deal of general relativity by simply picturing a curved space-time as a medium with a gradually varying refractive index," writes Ulf Leonhardt in the November 2013 issue of Nature Photonics.6
Earlier experiments showed that transformation optics could change refractive index in a way that mirrored gravitational effects, but they were not accurate enough for simulations. Now Dentcho Genov at Louisiana Tech University (Ruston, LA) and colleagues at the National Center of Microstructures and Quantum Manipulation (Nanjing, China) have modeled both far-field gravitational lensing and near-field light trapping using a microstructured optical waveguide and microsphere (see Fig. 3).7 They say high-index microstructures could serve as omnidirectional absorbers.
Stationary objects cannot simulate gravitational trapping within an event horizon, but moving materials can if they move faster than whatever is being trapped. "The horizon is the place where the velocity of the medium reaches the speed in the medium," says Leonhardt. For example, a fish trying to swim upstream would be trapped if it cannot swim faster than the water is flowing downstream. Likewise light could be trapped in a fast-moving medium with a refractive index n high enough to slow the velocity of light c/n below the velocity of the medium itself—modeling the behavior of a gravitational black hole.
Outlook
Optical singularities are fast approaching the technology stage. Swartzlander says they "are not just some exotic little phenomenon. By studying them deeper and deeper, you find a lot of uses." Like shifting between time and frequency domains to analyze signals, viewing wave interactions as singularities and vortices can be a powerful analytical tool for solving optical problems and can lead to new applications that otherwise would seem impossible, such as ways to control optical filamentation, improve communication channels, or directly observe Earthlike exoplanets. One fascinating concept is an optical black hole laser, which amplifies light trapped between two moving refractive-index perturbations simulating event horizons.8
Besides, it's fascinating to realize that optical singularities are crucial to such everyday wonders as watching bright and dark waves of light dancing on a shallow lake bed on a sunny day.
REFERENCES
1. W. Whewell, Researches on the Tides. - Sixth Series, 126, 238-336 (1836).
2. M. Berry, Nature V, 403, 21 (Jan. 6, 2000).
3. J. Wang et al., Nat. Photon., http://dx.doi.org/10.1038/ nphoton.2012.138 (2012).
4. G. Foo, D. M. Palacios, and G. A. Swartzlander, Jr., Opt. Lett., 30, 3308–3310 (2005).
5. E. Serabyn, D. Mawet, and R. Burruss, Nature, 464, 1018–1020 (April 15, 2010); doi:10.1038/nature09007.
6. U. Leonhardt, "Gravitational lens on a chip," Nat. Photon., 7 (Nov. 2013).
7. C. Sheng, H. Liu, Y. Wang, S. N. Zhu, and D. A. Genov, Nat. Photon., 7 (2013); doi:10.1038/nphoton.2013.247.
8. D. Faccio, T. Arane, M. Lamperti, and U. Leonhardt, Classical Quant. Grav., 29, 224009 (2012).
About the Author
Jeff Hecht
Contributing Editor
Jeff Hecht is a regular contributing editor to Laser Focus World and has been covering the laser industry for 35 years. A prolific book author, Jeff's published works include “Understanding Fiber Optics,” “Understanding Lasers,” “The Laser Guidebook,” and “Beam Weapons: The Next Arms Race.” He also has written books on the histories of lasers and fiber optics, including “City of Light: The Story of Fiber Optics,” and “Beam: The Race to Make the Laser.” Find out more at jeffhecht.com.