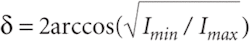Polarization metrology moves beyond 'home-brewed' solutions
MATTHEW SMITH
An ever-present engineering challenge in high-volume product development is to find the least expensive components with specifications that are “just good enough” for a product to function within specification when assembled. This task has been particularly difficult when it comes to polarization elements because of the lack of available polarization test equipment.
At the other end of the cost spectrum are engineers and scientists who design ultra-high-precision optical systems. These systems can require polarization elements with extremely tight tolerances, where a single out-of-specification part can cause system failure. And finding the offending component in a complex system is a difficult task without the proper metrology tools (see “Buyer beware”).
Testing polarization-testing optics
Throughout the industry, the most common form of polarization testing is based on “home-brewed” setups. Typically, these systems are built to measure a particular polarization property, and in most cases they work well.
A common system to measure the retardance of a waveplate, for instance, is made by rotating the waveplate in a collimated beam between two well-aligned linear polarizers. Careful measurement of the maximum and minimum collected power (Imax and Imin respectively) allows the retardance (δ) to be calculated as
While this technique can yield extremely accurate retardance measurements, it can’t differentiate between the fast and slow axes of the waveplate. Correctly identifying the fast axis is imperative in many applications, and manufacturers occasionally mark their waveplates incorrectly.
Furthermore, this simple retardance measurement technique gives the wrong retardance if the waveplate has an elliptical fast axis. The fast axis of a retarder defines the polarization state for which a beam of light propagates fastest through the retarder. The orthogonal polarization state necessarily propagates the slowest, and the retardance is the phase difference between these two states after propagation through the waveplate. For most waveplates, the fast axis is a linear polarization state, but in general, the fast axis can be any polarization state including linear, elliptical, or circular.
In cemented zero-order waveplates and in achromatic waveplates, an elliptical fast axis is an extremely common, but not widely known, defect. To first order, having a slightly elliptical fast axis is just like having a small optical rotation, as would be caused by some optical activity, following the waveplate. At Axometrics we are unaware of any manufacturer that publishes an optical rotation specification for their multiplate retarders.
And there are, of course, many other types of in-house polarization measurement systems designed for measuring parameters such as polarizer extinction ratio, polarizer transmission axis, and optical rotation. But these systems almost always make assumptions about the sample under test that, if incorrect, can produce erroneous measurements.
Mueller-matrix testing
The most comprehensive means of testing a polarization element is to measure its Mueller matrix. The Mueller matrix is a 4 × 4 matrix of a real-valued numbers that completely describes all possible polarization-altering properties of a sample for a particular optical beam (that is, a single wavelength or particular spectral distribution, a single incident angle or f/#, a particular position on the sample, and so on). In general, determining the Mueller matrix of a sample involves launching a variety of polarization states into the sample, and measuring the polarization state that emerges for each launched state. Several of these techniques have been described in the literature, and instruments for making Mueller-matrix measurements are now commercially available.1, 2, 3
Once the Mueller matrix of a sample is known, so is the manner in which the polarization state of light will change after propagation through the sample. And if the Mueller matrices of all the optical elements in the system are known, end-to-end system performance can be predicted, as can system sensitivity to variations and defects in polarization elements. However, being faced with the 16 numbers in a raw Mueller matrix is intimidating so it is more informative to perform some mathematical manipulations. Frequently, a polar decomposition of the Mueller matrix is performed.4 This operation breaks the Mueller matrix into the four fundamental polarization properties of retardance, diattenuation, polarizance, and depolarization.
Four basic polarization properties
The retardance of a sample describes the difference in phase between the fastest and slowest propagating polarization states. This phase difference can be expressed as an angle (in radians or degrees), or as a fraction of a wavelength (because there are 360° of phase in one wave, a quarter-wave retarder has 90° of retardance), or in units of length (typically nanometers). The fast axis is the polarization state that passes through the sample the fastest. This can be any polarization state: linear, elliptical, or circular.
Diattenuation (Diat) describes the difference in transmission (Tmax and Tmin) between different input polarization states, and is defined as:
Diattenuation can have values between zero and one, with Diat = 0 implying no difference in transmittance between various polarization states, and Diat = 1 implying total attenuation (through absorption or reflection) of one polarization state as in a perfect polarizer. Diattenuation is also described by a transmission axis that defines the polarization state that is maximally transmitted. This axis is frequently a linear polarization state, but in general can be any polarization state on the Poincaré sphere. Note that the minimally transmitted polarization will always be the orthogonal polarization state. The term diattenuation is frequently called polarizer efficiency, and can be converted into a variety of other terms including extinction ratio, contrast ratio, and polarization-dependent loss (PDL).
The polarizance is defined as the degree of polarization (DOP) of the transmitted light when unpolarized light is incident on the sample. A corresponding polarizance vector describes this output polarization state, and in general can be any polarization state on the Poincaré sphere.
It is interesting to note that the diattenuation magnitude and polarizance magnitude will be exactly the same if there are no depolarization effects in the sample. Conversely, if the diattenuation magnitude and polarizance magnitude are different in a sample, this always implies a depolarization effect.
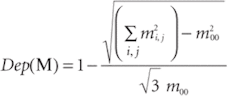
Depolarization effects are particularly complex to describe and interpret because different input polarizations are usually depolarized by different amounts. The depolarization index (Dep), defined for a Mueller matrix (M with elements mi,j) as
is something of a one-size-fits-all metric to identify the presence and magnitude of depolarization.5 Depolarization index can be in the range 0 ≤ Dep ≥ 1, where Dep = 0 implies no depolarization, and Dep = 1 implies a perfect depolarizer. Understanding all of the depolarization effects in the Mueller matrix remains an ongoing research topic in polarimetry.6
With a little practice, one can become skilled at quickly interpreting the whole of a sample’s polarization properties by looking at the four basic parameters of retardance, diattenuation, polarizance, and depolarization. And while it is true that for many samples, only one of these parameters will be significant, having metrology equipment that can measure all four parameters is important to identify unexpected polarization effects.
Measurements
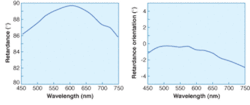
At Axometrics, we recently received a batch of Glan-Thompson polarizers intended for use in our polarimeter system. Glan-Thompson polarizers are known for their extremely high extinction ratio. They are manufactured by cementing two calcite prisms together. Our incoming quality-control inspection revealed a serious defect in one of the parts. The input polarizer axis was oriented horizontally (as expected), however the output polarizer axis was oriented at 5.6° to horizontal. Expressed in terms of our four basic polarization properties, the diattenuation axis and the polarizance axis were separated by 5.6° (see Fig. 1 at top of this page). Effectively, this polarizer rotated the transmitted polarization state by almost 6°, which could seriously compromise the performance of many optical systems. The cause: a serious misalignment of the crystal axes in the one of the polarizer’s calcite prisms.Another popular polarization element is the polymer achromatic quarter-wave retarder based on the Pancharatnum design. These elements achieve nearly quarter-wave performance across a broad wavelength range (see Fig. 2). The retardance in the illustrated example is within 3° of quarter-wave from 425 to 725 nm. However, a little-known problem with this type of retarder is that even when perfectly manufactured, the fast-axis orientation varies as a function of wavelength. The orientation in the illustrated example also varies by about 2.5° across the visible spectrum. In some applications, this variation will be unimportant. But in many precision applications, such as achieving a good dark state in a liquid-crystal projector, detailed knowledge of this retardance axis variation is absolutely vital.
REFERENCES
1. R. M. A. Azzam, Opt. Lett. 2, 148 (1987).
2. G. E. Jellison, F. A. Modine, Appl. Opt. 36 8184 (1997).
3. S. Krishnan, P. C. Nordine, Appl. Opt. 33, 4184 (1994).
4. S.-Y. Lu, R. A. Chipman, J. Opt. Soc. Am. A 13(5), 1106 (1996).
5. R. A. Chipman, Handbook of Testing optics II, 2nd Ed., Ch. 22, M. Bass ed., McGraw-Hill, New York (1995).
6. R. A. Chipman, in Proc. SPIE 5158, 184; Polarization Science and Remote Sensing, Joseph A. Shaw, J. Scott Tyo Eds. (2003).
Matthew Smith is the chief technology officer at Axometrics, 515 Sparkman Dr., Huntsville, AL 35816; e-mail: [email protected].