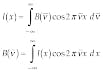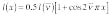Compact FT-IR spectrometers address real-world problems
The Fourier-transform infrared (FT-IR) spectrometer has, for many years, been the instrument of choice for the analysis of infrared spectra. In the laboratory, analytical chemists have grown to rely on these instruments for qualitative and quantitative analysis, in addition to the structural determination of complicated molecules. For example, the proceedings of the annual Pittcon meeting (March 1998; New Orleans, LA) and the Web sites of commercial FT-IR instrument manufacturers show the wide range of practical problems that can be addressed with these instruments. Unfortunately, the size, complexity, and cost of commercial FT-IR spectrometers has made it difficult to use them outside the laboratory.
Realizing that process and environmental monitoring represent large, untapped markets for FT-IR technology, several manufacturers have developed platforms that are smaller and easier to use than conventional laboratory instruments. This process has been aided substantially by optomechanical-design innovations and the continued development of dedicated hardware and software for data analysis and interferometer control.
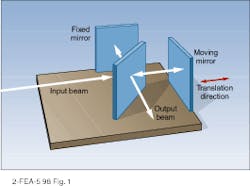
From an instrumental standpoint, FT-IR devices provide an excellent example of interferometry at work. Basically, an FT-IR spectrometer is nothing more than a movable-mirror Michelson interferometer that is equipped with a detector to monitor the output intensity (see Fig. 1). By plotting the detector output as a function of mirror displacement, one obtains a function that is related to the Fourier transform of the input spectrum. In a typical instrument, control of the mirror position, the measurement of output intensity, and the numerical calculations required to obtain a usable spectrum are performed by a microcomputer or custom digital-signal processing circuitry.This article examines the basic theory underlying Fourier-transform spectroscopy and briefly discusses the variables that affect spectral resolution and sensitivity. Subsequent sections deal with practical design issues and the directions for future engineering improvements.
Advantages in the infrared
Shortly after the invention of his amplitude-splitting interferometer, Michelson realized that it could be used to analyze complicated spectra. To better understand this capability, we first look at an idealized case where the instrument of Fig. 1 is illuminated by the perfectly collimated output of a single-frequency laser. When the instrumental response function is neglected and the mirrors are perfectly aligned, translation of the mirror on the right side of the figure results in a sinusoidal intensity variation at the detector that is described by the following expression1
[1]
where n-- is the input wavenumber, I(n--) is the source spectrum, and x is the displacement of movable mirror from the position of zero phase difference. When the instrument spectral response is included and the dc term neglected we find that
[2]
This expression is, however, the definition of the cosine Fourier transform indicating that the interferogram described by I(x) is equal to the Fourier transform of the input spectrum, weighted by the spectral response of the instrument.
In those cases in which multiple input frequencies are present, the output is equal to the integral of the contributions of each of the individual input frequencies. The resulting Fourier transform pair defines the relationship between I(x) and B( n--)
In a Fourier-transform spectrometer, the input spectrum is computed by digitizing the output intensity variation as the mirror is moved over the displacement range of the instrument. The resulting interferogram corresponds to I(x) in the above equation, and the input spectrum is calculated by computing its Fourier transform and subtracting out the known spectral properties of the instrument from the resulting B(n--) function. The instrumental response is determined from a knowledge of instrumental parameters and/or measurement of a known reference spectrum.
In a real interferometer, the movable mirror can only be translated through a finite distance, and it is impossible to evaluate the integral in Eq. 3 between infinite limits. While this fact fixes the theoretical wave number resolution of any instrument to a value that is approximately equal to the reciprocal of the translation range, the accuracy required for most practical applications can be achieved with relatively short translations. For example, gas-phase process monitoring requires a resolution between 0.2 and 2 cm-1 corresponding to approximate translation distances between 5 and 0.5 cm, respectively.
A more thorough analysis of the effect of finite translation distance on the interferogram recorded by an FT-IR spectrometer shows that secondary maxima are also produced. In commercial instruments, the magnitude of these secondary maxima is reduced by numerically weighting the interferogram with an apodization function. Numerous functions have been used for this purpose, each having certain trade-offs with respect to resolution and sensitivity.
Misalignment reduces resolution
While the basic theory of the Fourier-transform spectrometer is relatively straightforward, the practical design issues associated with fielding a commercial instrument are formidable. In a Michelson interferometer, the maximum resolution and accuracy are achieved when perfectly aligned mirrors are illuminated with a perfectly collimated source. Deviations from perfect collimation result in a circular fringe pattern at the output, and failure to limit the source image to the central fringe washes out the interferogram. For a fixed input wavelength, the radii of the output fringes are inversely proportional to the displacement of the movable mirror, and the divergence of the input source determines translation range over which an interferogram can be recorded. Mathematically, the acceptance half-angle of the instrument is approximately equal to the square root of the wavenumber resolution of the instrument divided by the maximum wavenumber in the source spectrum.
Mirror misalignment significantly reduces the contrast of the output fringes and can result in distorted line shapes. These effects are the most pronounced at high wavenumbers (short wavelengths), where misalignment can completely wash out the spectrum. The optomechanical problems associated with maintaining mirror alignment as an interferometer is repetitively cycled over its range of motion are formidable and partially dependent on the environment in which the FT-IR spectrometer is located. Laboratory instruments typically experience a narrower range of temperatures and are subjected to less vibration than those used for process and environmental monitoring. The major commercial instrument manufacturers have each spent a significant amount of development time designing ruggedized interferometers. Once developed, these designs form the basis of an entire family of instruments with similar resolution and stability.
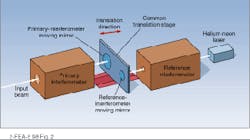
In addition to careful optomechanical design, instrument stability also can be increased through the use of active control of the mirror alignment. In a "dynamic alignment" approach used by Bomem (Quebec City, Canada), a HeNe laser beam is injected along the axis of the interferometer. By monitoring the shape of the HeNe interference pattern, it is possible to monitor the mirror alignment while the instrument is in operation and to correct for deviations from parallelism using piezoelectric elements on the fixed mirror. This feature was first incorporated into the company`s research instruments, making it possible to maintain accurate mirror alignment over comparatively long translation distances with a resulting increase in instrumental resolution.
Helium-neon lasers are also used to monitor the position of the moving mirror (see Fig. 2). In this scheme, a second mirror is mounted on the carriage used to translate the moving mirror of the measurement interferometer. This mirror is used as the moving element of a second reference interferometer that is illuminated by the output of a HeNe laser. By counting fringes at the output of this interferometer, it is possible to determine the relative position of the interferometer carriage (and hence the mirror of the primary interferometer) to subwavelength accuracy. The absolute location can be determined using a white-light input to the reference interferometer, thereby generating a narrow peak at the zero relative-displacement position.In addition to the Michelson design of Fig. 1, there are a number of other interferometer types used for specialized FT-IR applications. While a description of these designs is outside the scope of this article, they each have specialized advantages with respect to certain measurement parameters. In some cases, these advantages have to do with the long-term stability of the design, while in others they lead to increased measurement speed and/or resolution. For example, corner cubes have been used in place of plane mirrors in the basic Michelson design. Although more difficult to align initially, corner-cube reflectors significantly reduce the effect of mirror tilt on instrument performance.
Ruggedized FT-IR systems
While FT-IR instruments will continue to be manufactured for the research and analytical-laboratory markets, significant growth can only be achieved by moving FT-IR technology into the various applications found in the real world. Of particular interest are applications in industrial-process and environmental monitoring. This fact is recognized by a number of major instrument manufacturers who have developed small, ruggedized instruments for these applications.
A good example of this type of instrument is the Nicolet Avatar (see photo at top of this page). According to the manufacturer, this spectrometer is designed for a nonexpert end user, incorporating kinematically aligned optical subassemblies that can be changed without alignment. In addition, integrated monitors and fault-analysis software watch the performance of the instrument during operation, notifying the user of potential measurement errors. Based on a ruggedly constructed, dynamically aligned interferometer with a maximum resolution of 0.5 cm-1, the design is compatible with a number of input assemblies that allow the basic instrument to be used for a wide range of applications.
Instruments such as the Avatar reflect current trends in FT-IR design. Taking advantage of the rapid and continued progress in digital-signal processing (DSP) and computer hardware, the on-board electronics that are built into newer instruments do much more than calculate the Fourier transform of the output interferogram. In addition to continuously monitoring the instrument performance, they also provide output data in a form that is directly usable for particular applications. For example, the variable of interest in a process-monitoring application is not the sample spectrum but the numerical value of certain variables that are required to control the process. By programming custom data-analysis capabilities into an FT-IR instrument, the values of these variables can be output directly.
In addition to the development of customized software, interface modules are continuing to be developed for a wide range of applications. For example, Applied Spectral Instruments (Danbury, CT) has recently developed a diamond probe that allows an FT-IR instrument to be interfaced directly with a liquid process stream. This is significant because, in many cases, liquid processes take place at high temperatures and can involve corrosive chemicals. The diamond probe combines high transmission throughout the infrared region with immunity to both heat and chemical degradation.
Looking forward, one can expect the continued development of hardware and software packages that will make FT-IR instruments both more powerful and easier to use. In addition, new interface modules will allow a basic instrument to be used for a wide range of applications. Progress in the area of interferometer design is expected to be slower and less dramatic than with DSP and interface capabilities. This is partially due to the maturity of the base technology in addition to the expense associated with re-engineering the heart of the machine. Cost reductions will be the result of increased volume rather than major design advances and will hopefully accompany the increased use of FT-IR spectrometers for process monitoring and other applications outside the chemical laboratory.
ACKNOWLEDGMENTS
The author wishes to thank Don Sting of Applied Spectral Instruments (Danbury, CT), Chris Petty of Nicolet Instruments (Madison, WI), and Luc Rochette and Carl Mercier of Bomem/Hartmann & Braun (Quebec City, Quebec, Canada) for helpful discussions during the preparation of this article.
REFERENCE
1. Peter R. Griffiths and James A. de Haseth, Fourier Transform Infrared Spectrometry, Wiley, New York, NY (1986).