ADVANCES IN IMAGING: Fresnel incoherent correlation holography (FINCH): A different way of 3D imaging
JOSEPH ROSEN and GARY BROOKER
Holographic imaging offers a reliable and fast way to capture the complete 3D information of a scene from a single perspective. However, because white light is incoherent, holography is not widely applied to white-light imaging; in general, creating holograms requires a coherent interferometer system.
Here, we summarize seven years of research into a new method we invented for acquiring incoherent digital holograms. The term incoherent digital hologram means that incoherent light beams reflected or emitted from real existing objects interfere with each other. The resulting interferograms are recorded by a digital camera and digitally processed to yield a hologram. This hologram is reconstructed in the computer so that 3D images appear on the computer's screen.
The coherent optical recording of a classical holographic system is not applicable to incoherent objects, because interference between incoherent reference and object beams cannot occur. To generate incoherent digital holograms, a different holographic acquisition method is required.
Our incoherent digital hologram method is dubbed Fresnel incoherent correlation holography (FINCH). This approach is actually based on a single-channel, on-axis, incoherent, self-referenced interferometer. Like any Fresnel holography, in FINCH the object is correlated with quadratic phase functions, but the correlation is carried out without any scanning and without multiplexing the image of the scene.
FINCH can operate with a wide variety of light sources, and in principle could be made to work at any wavelength in the electromagnetic spectrum. Because of this flexibility, it can be used in high-resolution holographic applications that were not possible in the past because they were limited by the need for coherent laser light.
SLM-created diffractive element
FINCH makes use of the fact that every incoherent object is composed of many uncorrelated source points, each of which is self-spatially coherent and can therefore create an interference pattern with light coming from the point's mirrored image. Each interference pattern is in a shape of Fresnel rings, and thus the overall effect is of a set of rings projected onto the plane of a camera for each and every point at every plane of the object being viewed.
The depth of the object points is encoded by the density of the rings such that points closer to the system project rings that are denser than those from distant points. As a result, the 3D information in the volume being imaged is recorded by the digital camera. Therefore, each plane in the image space reconstructed from the Fresnel hologram is in focus at a different axial distance.
Our first published results in 2007 described a method to capture digital holograms of 3D objects illuminated by a white-light source.1 The basic setup of FINCH is simple and includes a collimation lens (in the case of a microscope, the objective), a spatial light modulator (SLM), a digital camera, and sometimes a few filters and polarizers. The principle of operation is also simple: Incoherent light emitted from each point in the object being imaged is split by a diffractive element created by the SLM into two beams that interfere with each other. The camera records the entire interference pattern of all the beam pairs emitted from every object point, creating a hologram.
Typically three holograms, each with a different phase constant encoded into the pattern of the diffractive element, are recoded sequentially and are superposed in a computer in order to eliminate the unnecessary bias illumination and the twin image from the reconstructed scene. The resulting complex-valued Fresnel hologram of the 3D scene is then reconstructed on the computer screen by the standard Fresnel back-propagation algorithm. Acquiring only three holograms is enough to reconstruct the entire 3D observed scene such that, at every depth along the z-axis, every object is in focus in its image plane.
Since 2007, we have been involved with several works on this topic, including color fluorescence FINCH,2 a study on a FINCH-based microscope,3 a method to suppress noise in FINCH,4 a polarization-based technique to split the incoherent light more efficiently,5 ways to improve the imaging resolution,6, 7 a method to extend the FINCH bandwidth,8 and FINCH operating in a synthetic-aperture mode.9,10 In the following sections we summarize some of these milestones of the short history of FINCH.
Fluorescence microscopy
A microscopy system based upon FINCH was used to record high-resolution 3D fluorescent images of biological specimens. Using high-numerical-aperture lenses, an SLM, a CCD camera, and some simple filters, the FINCH-based microscope enables the acquisition of 3D microscopic images without the need for scanning.
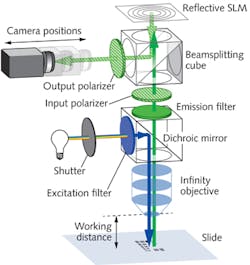
A diagram of FINCH for an upright microscope equipped with an arc-lamp source is seen in Fig. 1. The beam of light that emerges from an infinity-corrected microscope objective transforms each point of the object being viewed into a plane wave. A filter wheel was used to select excitation wavelengths from a mercury-arc lamp, and the dichroic mirror holder and the emission filter in the microscope were used to direct light to and from the specimen through infinity-corrected objectives.
As mentioned previously, the SLM in FINCH is responsible for splitting the beam coming from each and every object point. The beam is split by two different diffractive elements displayed on the SLM: one a constant valued phase distribution, and the other a transparency distribution of a positive spherical lens.
We have experimented with two methods to display these two elements on the same SLM. The older, and less efficient, method is to randomly allocate half of the SLM pixels to each of the two masks. The use of a constant phase mask presents certain disadvantages in that it requires the use of half the pixels on the SLM, and also degrades the resolution of the mask that creates the spherical wave.
More recently, we have learned that a better approach is to use a positive lens mask that covers all the SLM pixels, along with light having two mutually orthogonal polarization components, one parallel to the polarization of the SLM and the other orthogonal to it. As a result, the interference happens between the projections of each polarization component of the light beam on the crossing angle between the two orthogonal polarizations.
Superresolution
In 2011 we discovered, to our surprise, that under specific conditions, FINCH can exceed standard incoherent optical imaging-system resolution and is thus superresolving. Based upon analysis of FINCH using tools of linear-system theory, we have shown that FINCH is actually a hybrid between a coherent and an incoherent system, demonstrating the resolution advantages inherent in each.
In coherent optics, there is a sharp cutoff of the modulation-transfer function (MTF) but its bandwidth is narrow. Incoherent optics have a wide MTF; however, the cutoff is not sharp. FINCH has an MTF cutoff that is sharp and wide at the same time.
Coherent optics have a wider point-spread function (PSF) than incoherent optics, while FINCH ends up having an even narrower PSF than incoherent systems. Thus, FINCH is a hybrid system with a resolution superior to the two other imaging types. Optimal FINCH resolution is also dependent on its configuration and on the ratio between the distance from the SLM to the camera and the focal length of the diffractive lens displayed on the SLM.
For all possible configurations, the condition for maximum resolution occurs when there is a perfect overlap between the projections of the two different interfering beams (originating from the same point source) at the camera sensing plane. Under this optimal condition, FINCH can resolve better than a coherent holographic system by a factor of two, and better than a conventional lens-based incoherent imaging system by a factor of about 1.5.
The issue of coherence in relation to FINCH has been studied. FINCH is a spatially incoherent holographic imaging system that can work well only if some level of temporal coherence exists. In the past, with the setup of a single diffractive lens and the constant-phase mask, the maximum optical path difference (OPD) in the system was longer than the coherence distance of the light sources; hence, to get a hologram with a reasonable fringe visibility, we did one or both of the following actions: We narrowed the source bandwidth with a chromatic filter to increase the temporal coherence of the system, or we increased the SLM-to-camera distance to interfere with the waves inside the high temporal coherence regime.
Both actions have high prices, and they both can be avoided by use of dual-lens FINCH. The values of the SLM-camera distance and the source bandwidth in comparison to FINCH with a single diffractive lens show a considerable improvement. These improved values enable the detection of weaker radiating objects over a much wider field of view.
Once the source bandwidth and the SLM-camera distance (and consequently the image magnification) are given, the upper limit on the value of the gap between the two focuses of the two diffractive lenses can be easily calculated. Working in the range below this upper limit guarantees relatively high coherence and consequently high fringe visibility for the recorded holograms. Because the optical path difference between beams can be minimized using dual-lens FINCH, the fluorescence emission can be of relatively wide bandwidth.
Some of the results from the many experiments carried out by our group during the last seven years with various configurations of FINCH are shown in Fig. 2. It should be noted that at least two other groups have further developed the idea of FINCH for the applications of vortex imaging and adaptive optics.11, 12
Because FINCH does not scan the object in either space or in time, it can generate holograms rapidly with a better resolution than classical imaging systems. FINCH enables the observation of a complete volume from a hologram, potentially enabling objects moving quickly in three dimensions to be tracked. The FINCH technique shows great promise for rapidly recording 3D information in any scene, independently of the illumination.
ACKNOWLEDGMENTS
This work was supported by The Israel Ministry of Science and Technology (MOST) to JR and by NIST ARRA Award No. 60NANB10D008 to GB and by Celloptic Inc.
REFERENCES
1. J. Rosen and G. Brooker, Opt. Lett., 32, 912–914 (2007).
2. J. Rosen and G. Brooker, Opt. Expr., 15, 2244–2250 (2007).
3. J. Rosen and G. Brooker, Nat. Photon., 2, 190–195 (2008).
4. B. Katz et al., Appl. Opt., 49, 5757–5763 (2010).
5. G. Brooker et al., Opt. Expr., 19, 5047–5062 (2011).
6. J. Rosen et al., Opt. Expr., 19, 26249–26268 (2011).
7. N. Siegel et al., Opt. Expr., 20, 19822–19835 (2012).
8. B. Katz et al., Opt. Expr., 20, 9109–9121 (2012).
9. B. Katz and J. Rosen, Opt. Expr., 18, 962–972 (2010).
10. B. Katz and J. Rosen, Opt. Expr., 19, 4924–4936 (2011).
11. P. Bouchal and Z. Bouchal, Opt. Lett., 37, 2949–2951 (2012).
12. M.K. Kim, Appl. Opt., 52, A117–A130 (2013).
Joseph Rosen is with the Department of Electrical and Computer Engineering, Ben-Gurion University of the Negev, Beer-Sheva, Israel; e-mail: [email protected]. Gary Brooker is with the Department of Biomedical Engineering and Microscopy Center, Johns Hopkins University, Rockville, MD; e-mail: [email protected].