Photonic Frontiers: Entangled photons: ‘spooky action’ works at a distance
One of the most bizarre predictions of quantum mechanics is that a pair of particles can become entangled, which means that measuring the properties of one particle instantly determines the state of the second no matter how far apart the two are. A simple example of entanglement is a pair of electrons produced with two spin states superimposed. Quantum mechanics tells us that each particle’s spin is unknown until measured, but because the two particles must have opposite spins, measuring the spin of one instantly tells us the other particle’s spin.
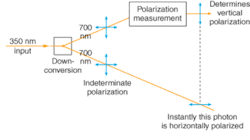
Pairs of photons can be entangled when they are generated by nonlinear down-conversion, which splits one short-wavelength photon into two longer-wavelength photons with the same total energy, or when they are simultaneously put into a space where they cannot be distinguished from one another. The most common entangled property is polarization; measuring polarization of one photon instantly determines that the second photon has the orthogonal polarization. As with electrons, this implies the existence of an instantaneous link between the two entangled photons that tells the second photon what its polarization should be (see Fig. 1). Note that polarization resolves into a pair of states, vertical and horizontal or right- and left-circularly polarized, yielding the binary values needed for quantum computing and cryptography.
Photons can also be entangled in their other degrees of freedom-energy and momentum. Energy does not have to be split evenly between photons, but the sum of the two energies must equal the energy of the original photon; equivalently, this can be viewed as entanglement in the time the photons are emitted. Entanglement of photon momentum covers their linear, orbital, and transverse spatial modes, so it also involves more possible states than polarization.
This sort of quantum weirdness bothered Albert Einstein, who called it “spooky action at a distance.” In a 1935 paper he, Boris Podolsky, and Nathan Rosen described a thought experiment in which entanglement created a paradox that he considered fatal to quantum mechanics because it required transmitting information faster than the speed of light from the measured particle to the second particle. But experiments have verified entanglement, validating quantum mechanics and leading to demonstrations of how “spooky action” can be used for applications such as quantum cryptography, but classical signals still can’t be sent faster than the speed of light.
Improvements in entanglement
Processes such as down-conversion tend to be inefficient, and the early sources could generate entangled pairs only at very low rates. But source brightness-measured in pairs detected per second-has increased at Moore’s Law rates for two decades, says Paul Kwiat of the University of Illinois at Urbana-Champaign. His group recently produced more than two million measured pairs per second.1
Photon pairs can be entangled in more than one degree of freedom. Although most experiments entangle only one degree of freedom, some have simultaneously entangled two properties. Kwiat’s group reports that it has generated and measured the properties of photon pairs “hyperentangled” in all three degrees of freedom, allowing them to characterize the largest quantum system yet studied.2
Other groups have demonstrated entanglement of three, four, and recently five photons.3 Multiphoton entanglement allows operations that are more complex than those possible with two photons, such as the quantum “teleportation” described below and quantum communications among more than two people.
Other experiments have transferred entanglement between photons and atoms, a process that is important for applications such as quantum computing because atoms are better for storage, “but the only thing that can easily move around is a photon,” says Franco Wong of the Massachusetts Institute of Technology. In one important test, a cadmium atom was entangled with a photon it spontaneously emitted.4 Entanglement is rugged enough to survive being converted into a surface plasmon, and then back into a photon, although the efficiency is low, losing many photons in the process.5
Quantum cryptography
Originally developed around the principle that measurements inevitably affect the properties of the object being measured, quantum cryptography can be made stronger by using entangled photons. Without entanglement, data bits can be transmitted as single polarized photons. Measurements by an eavesdropper would inevitably affect the single photon’s polarization in a way that in principle the two people using the system could detect. However, true single-photon sources are hard to make, and the system is vulnerable to tapping if it simultaneously transmits two photons to the receiver or if the bit being sent leaks to other degrees of freedom. The use of entangled photons can create a self-checking source.In 1991, Artur Ekert, now at the University of Cambridge (England) proposed splitting a pair of entangled photons, sending one to each of the two people exchanging information.6 The two have polarizers aligned so that if one person detects an entangled photon, the other will detect the other member of the entangled pair. Although the polarization of the second photon is determined the instant the first photon is detected, neither person can predetermine the results of their measurement, so this arrangement can’t transmit information faster than the speed of light. One or both of the people can miss some photons, but they can use protocols to identify the roughly half of the data that is perfectly correlated and detect any possible eavesdropping.
In practice, the low rate of generating photon pairs limits the speed of entanglement-based quantum cryptography, so it would transmit digitally secure encryption keys to decode encrypted data sent over a public communication channel. Both entangled and unentangled approaches have been demonstrated in the laboratory. In 2004, a team from the University of Vienna (Austria) used polarization-entangled photons to send a secure quantum key between the Vienna City Hall and a large bank through 1.45 km of fiberoptic cable laid through the city’s sewer system.7 They tested the arrangement by using it to transfer a €3000 donation to the lab’s bank account (see Fig. 2).Quantum teleportation and more
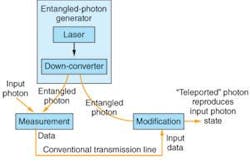
Entangled photons can also perform quantum “teleportation,” which transfers the quantum state of a photon to a distant site. In quantum-mechanical terms that is considered teleportation, although it doesn’t transfer the photon energy. Likewise, the state of ions can be teleported, although instantaneously moving mass remains in the realm of science fiction.
Quantum teleportation starts with a pair of entangled photons. The sender combines an input photon with one of the entangled photons and measures the combined quantum state. That measurement instantaneously puts the second entangled photon into a quantum state that contains complete information on the input photon, but has been rotated in a way that depends on the measurement outcome. Sending information about the measurement through a conventional telecommunication channel and the second entangled photon through a separate optical fiber allows the receiver to replicate the state of the input photon (see Fig. 3). Last year, a group from the University of Vienna used this approach to “teleport” photons to a receiver 600 m away.8 Their goal is to develope a full-scale quantum repeater, the quantum counterpart of an optical repeater.
Outlook
Current experiments have significant limitations. Entangled pairs must be generated at low rates to produce the right quantum properties. Although new techniques have multiplied the generation rate, a rate of two million pairs per second corresponds to average power only on the order of an attowatt! Multiphoton entanglement produces even lower powers because it requires a multistage process that is inevitably less efficient than entangling a pair of photons. Thus, actual speeds are very low; the Vienna teleportation experiment averaged 0.04 photon per second.
But progress is being made, and entanglement holds out other exciting prospects. Increasing the number of entangled photons produces states with a multiple of the photon energy, which can generate interference effects at a corresponding fraction of the wavelength, beating the diffraction limit.9, 10 Other potential applications include providing input for quantum-computing elements and high-resolution sensing.
REFERENCES
1. J.B. Altepeter et al., Optics Express, in press (2005).
2. J.T. Barreiro et al., to be published in Phys. Rev. Lett.
3. Z. Zhao et al., Nature430, 54 (July 1, 2004).
4. B.B. Blinov et al., Nature 428, 153 (March 11, 2004).
5. E. Altewischer et al., Nature 418, 304 (July 18, 2002).
6. A.K. Ekert, Phys. Rev. Lett. 67, 661 (1991).
7. A. Poppe et al., Optics Express 12, 3865 (Aug. 9, 2004).
8. R. Ursin et al., Nature 430, 849 (Aug. 19, 2005).
9. M.W. Mitchell et al., Nature 429, 161 (May 13, 2004).
10. P. Walther et al., Nature 429, 158 (May 13, 2004).
About the Author
Jeff Hecht
Contributing Editor
Jeff Hecht is a regular contributing editor to Laser Focus World and has been covering the laser industry for 35 years. A prolific book author, Jeff's published works include “Understanding Fiber Optics,” “Understanding Lasers,” “The Laser Guidebook,” and “Beam Weapons: The Next Arms Race.” He also has written books on the histories of lasers and fiber optics, including “City of Light: The Story of Fiber Optics,” and “Beam: The Race to Make the Laser.” Find out more at jeffhecht.com.