LASER THEORY: Ten-year-old embarrassment leads to unified laser theory
Ten years ago, when a team of researchers led by Claire Gmachl and Federico Capasso at Bell Laboratories (Murray Hill, NJ) grabbed the cover of Science magazine with a paper on “bow-tie” microcavity lasers, they also uncovered what one of their coauthors, A. Douglas Stone of Yale University (New Haven, CT), described as an “embarrassing” theoretical limitation. Now Stone and another team have devised a solution.
Stone’s group tested the new approach on perhaps the most theoretically challenging laser available, a diffusive random laser (DRL). And in doing so, the team seems to have found the missing theoretical link between emerging nanolaser technology and the theoretically tractable resonators that brought the first lasers into being four decades ago.1
Conventional laser theory by and large builds upon the ideal case of a Fabry-Perot interferometer cavity in which the laser frequencies follow from a simple interference condition on the waves between the mirrors. The basic theory treats the nonlinear medium as a two-level laser and solves Maxwell’s equations for an idealized system, in which the modes are all orthogonal to and independent of one another, and have infinite lifetimes.
Initially, such idealized theory may have seemed as if it would extend into the microscopic world of whispering-gallery lasers as well. But when Gmachl, Capasso, Stone, and colleagues slightly deformed the perfect circle of a whispering-gallery laser into the shape of a flattened ellipse, new “bow-tie” modes lit up and the electrical field pattern changed dramatically, while the output power of the device ballooned by three orders of magnitude.2 Despite the groundbreaking science that led to these seminal advances in laser technology, Stone, a theoretical physicist, was struck by the lack of a theory for predicting such impressive developments.
“This posed an embarrassment for theory because it wasn’t something we could predict,” he said. “We were actually stuck with ‘post-diction,’ and with qualitative rather than quantitative analysis, because the mode behavior was not as simple as with conventional laser structures.”
In the last 10 to 15 years, more and more realistic simulations of Maxwell’s equations and nonlinear polarization have been developed to provide increasingly accurate characterizations of modal behavior, Stone noted. But these methods were still focused on relatively simple resonator designs and used time-dependent simulations, which could be as difficult to interpret as the experiments, and still could not provide the predictive capabilities and physical insight that Stone was seeking.
Modern formulation of semiclassical theory
After initial publication in Science magazine 10 years ago, Stone and colleagues began to work on a comprehensive laser theory that would be predictive and would work for arbitrarily complex laser resonators, even when nonlinear effects were strong. The ultimate result was a modern formulation of standard (“semiclassical”) laser theory treating the common multimode situation, in which biorthogonal functions, which they called “constant flux states,” replaced the idealized linear cavity resonances of conventional laser theory.
“Tell me what your resonator is and a few things about your active material and how you are pumping it, and I’ll be able to predict the output power as a function of the pump, the number of lasing modes, the lasing frequencies, which modes actually turn on first, and the spatial dependence of the electric field inside and outside the resonator,” Stone said.
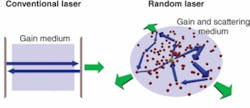
The team had initially planned to test its new approach on dielectric-cavity lasers like the 1998 bow-tie laser, but decided instead to demonstrate it on the most unconventional laser yet developed, the DRL. Such lasers consist only of light-scattering nanoparticles embedded in a gain medium; according to conventional laser theory, they appear to lack (in addition to any predictive theory of operation) the light-confinement mechanisms that are essential for efficient light amplification (see figure). In addition to their extreme leakiness, there is no simple interference condition on closed light paths to predict their frequencies, which differ for each arrangement of nanoparticles.
Developing a theory for the DRL required the researchers to do away with the simplifying assumption (at the heart of conventional laser theory) that the laser is a closed or finite system, as opposed to an open system, with energy flowing directly out to infinity.
“Because of this, people originally thought that the random laser must be different from conventional lasers, but Hui Cao (formerly at Northwestern University, now at Yale) demonstrated that they are not different in their lasing properties,” Stone said.3 “So this laser with the weirdest ‘cavity’ imaginable showed us that the real question is: What does the average electric field look like in a laser that is well above threshold with many modes emitting light and (in this case) many resonances contributing to each mode? These lasing modes would be very different. We couldn’t deal with this previously because of the openness of the systems, the complexity and the nonlinearity. Now we can.”
Their results on DRLs may have implications for the physics of chaotic waves in nonlinear media with gain. Similar questions also arise with more conventional lasers, and the team has recently shown in unpublished work that their theory predicts almost perfectly the results of time-dependent simulations of the Maxwell-Bloch lasing equations for simple edge-emitting laser structures. Eventually the researchers hope to replace the time-dependent simulations using their ab initio approach, thereby making arbitrarily complex laser systems accessible to precise and predictive theoretical design.
REFERENCES
1. H.E. Türeci et al., Science 320, 643 (May 2, 2008).
2. C. Gmachl et al., Science 280, 1556 (June 5, 1998).
3. H. Cao, J. Phys. A: Math Gen. 38, 10497 (Dec. 9, 2005).
Hassaun A. Jones-Bey | Senior Editor and Freelance Writer
Hassaun A. Jones-Bey was a senior editor and then freelance writer for Laser Focus World.