Few-cycle laser pulses control phase
The periods of electrons revolving in atomic orbitals fall in the attosecond (as) time scale—a domain that, until recently, was not accessible to the experimenter. If recent research results bear fruit, events in the attosecond range may someday be studied by stroboscopic means similar to those that make the spoke wheels of a stagecoach in a movie stand still.
Electronic wave packets perturbed by femtosecond optical fields are known to give rise to higher-harmonic pulses up to the soft x-ray region, with pulse durations reaching the attosecond regime. To optimize attosecond pulse generation, it is highly interesting to study femtosecond-pulse interaction with matter under well-defined conditions.
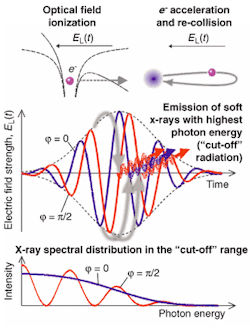
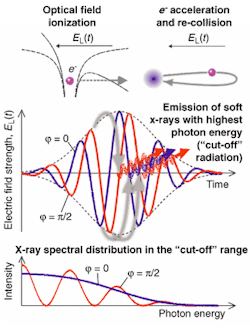
When a pulse lasts only a few optical cycles, the carrier-envelope phase relation becomes important for light pulses interacting with matter. Within the envelope, the actual trace of the carrier electromagnetic field fluctuates from pulse to pulse. During a pulse, maximal field strength will be obtained when the maxima of the optical carrier and of the envelope coincide (see Fig. 1). Although this phenomenon was recognized a few years ago, experimental control of the phase could not then be achieved.
Now, a team formed by the groups of Ferenc Krausz of Vienna University of Technology (Vienna, Austria) and Theodor Hänsch of the Max-Planck Institute for Quantum Optics (Munich, Germany) has combined recent achievements in short-pulse laser technology and frequency metrology to approach the goal of phase control.1 They succeeded in providing a phase-locked laser system supplying 5-fs, 0.5-mJ pulses at a 1-kHz repetition rate. Using this system, the researchers photo-ionized atoms under definite phase conditions, thus generating electronic wave packets, the motion of which could be controlled on timescales shorter than 250 as.
The key component of the phase-locked laser system is a 10-fs oscillator of 80-MHz pulse repetition rate consisting of a Kerr-lens mode-locked Ti:sapphire oscillator followed by a multipass amplifier. It is also followed by a device termed by the authors a "f-to-2f" interferometer, which was derived from a frequency-comb setup created by the Munich group (see Laser Focus World, July 2001, p. 38). The device coherently broadens the femtosecond-laser spectrum beyond an octave so that a beat signal can be obtained between a spectral component at the high-frequency end of the pulse and another component obtained by frequency doubling the low-frequency end of the same pulse.
Frequency doubling is performed in one arm of a Mach-Zehnder interferometer (hence the term f-to-2f interferometer). The phase detector applied at the output of the f-to-2f interferometer does not provide the absolute phase value but, together with phase-locking electronics, stabilizes the carrier-envelope phase; as the net result, every fourth pulse in the 80-MHz pulse train and, hence, every 80,000th pulse picked by the multipass amplifier, shows the same carrier-envelope phase. Phase drifts suffered during amplification are detected by a second f-to-2f interferometer whose output is taken into account in the total phase stabilization, yielding phase-locked and phase-controllable 5-fs pulses with 1-kHz repetition rate that are used for the experiments.
Detecting phase from photoionization
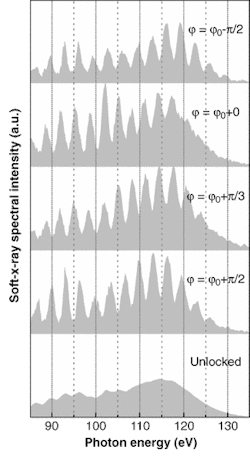
However, there is no direct method to detect the absolute value of the phase. Instead, the authors used the photoionization experiment itself to draw conclusions on it. By gently focusing the pulses onto a 2-mm-long sample of neon gas (at a pressure of about 160 mbar) soft x-rays were obtained. Blocked from visible radiation and lower harmonics generation by a thin zirconium foil, the spectrum of the higher harmonics was measured up to the cut-off using a grating spectrometer (see Fig. 2). The cut-off frequency or energy depends on the maximum energy the photoelectrons can gain in the optical field.
The intuitive picture of x-ray generation is that the optical electric field distorts the Coulomb potential of an atom so that an electron is released, pulled away from the ion, and accelerated by the electric field of the light wave. Since the field quickly reverses its direction, the electron can return to the ion where it can radiate the accumulated energy. The electric-field strength can be set by the focusing geometry in such a way that the ionization threshold is exceeded around a few field maxima only. It then becomes possible to adjust the carrier envelope phase so that only a single flash of soft x-ray radiation is produced during a laser pulse. In this case, the radiation spectrum near the cut-off energy turns into a smooth continuum and the maxima at high harmonic frequencies disappear.
Five spectra were obtained either with different phase settings or with the phase stabilization turned off (see Fig. 2). From the variations in the spectral shape, the authors conclude that they have controlled the envelope-carrier phase with a precision of better than π/5, corresponding to a change in timing of the electronic wave packets with respect to the pulse peak by only 250 as.
REFERENCE
- A. Baltuska et al., Nature 421, 611 (Feb. 6, 2003).