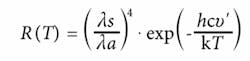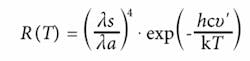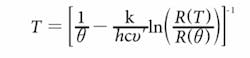FIBER-OPTIC SENSING: Self-calibrating technique enables long-distance temperature sensing
CHUNG E. LEE
Optical fibers have been used as a major tool in telecommunications for decades. But recently, the adoption rate of fiber-optic sensors and sensing technologies has grown rapidly because of unique advantages over other measurement devices and methods.1 Fiber-optic sensors offer the capability of handling much higher bandwidth and reduced operational risk (no electrical shocks or sparks), and optical fiber is inherently immune to electromagnetic interference (EMI) and does not emit EMI.
The most prominent feature of Raman distributed temperature sensing (DTS) is its ability to provide true distributed parameter monitoring. Utilizing DTS technology, temperature profiles, including distance information, can be monitored along the entire length of the sensing fiber-over 15 km. Distributed temperature monitoring provides information equivalent to tens of thousands of conventional point temperature sensors with simplified deployment and lower operational costs. Thus, Raman DTS provides an economical means of long-distance temperature monitoring.
Spontaneous Raman scattering
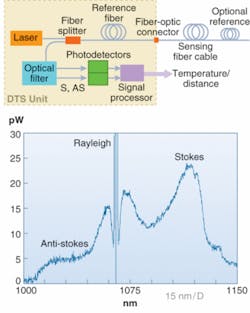
When an optical fiber is pumped by a light source, most of the light is transmitted, but small portions of incident light are scattered along the fiber. They are categorized into Rayleigh, Raman, and Brillouin scatterings. In Raman scattering, two opposite scattered bands called Stokes and anti-Stokes are generated with respect to the pump spectrum. The intensity of anti-Stokes is highly dependent on temperature, as compared to the Stokes component, because of the Boltzmann energy distribution. The Raman temperature-sensing method is based on the ratio of anti-Stokes to Stokes scattering intensity as a function of distance along the sensing fibers (standard telecommunication fibers).
If the ratio between anti-Stokes and Stokes intensities is measured, the absolute temperature measurement can be obtained and their ratio R(T) can be given by Equation 1:
where λa , λs are anti-Stokes and Stokes wavelengths, υ >is their wave-number separation from the pump wavelength, h is Planck’s constant, c is the velocity of the light, k is Boltzmann’s constant, and T is the absolute temperature of the fiber core under measurement.
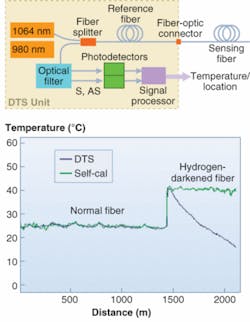
In a typical DTS, the laser output injected into the reference-fiber section is transmitted to a sensing fiber through a fiber splitter (see Fig. 1). The sensing fiber cable can be easily connected and disconnected with a fiber-optic connector. The backscattered portions from the reference and the sensing fiber are guided back to an optical filter via the same optical route. Then the Stokes and anti-Stokes components, separated by a filter, are fed to photodetectors to convert the optical signal to an electrical signal. Stokes intensity is a few times larger than anti-Stokes intensity and its bandwidth is usually much larger than the pump spectrum. Finally, the signal processor calculates the temperature profile along the sensing fiber.
To calculate the absolute temperature, the reference fiber is maintained under known temperature, θ. Then unknown temperature T along the arbitrary section of the fiber can be calculated from a rearranged equation written as:
where R(T) and R(θ) is the Raman backscattering ratio from an arbitrary section of the sensing fiber and from the reference fiber, respectively.2 An optional reference device can be installed on a sensing fiber for higher-accuracy operation.
To determine the position, time-domain and frequency-domain analysis have been applied. The time-domain method uses a pulsed source and the position of the temperature is identified by the calculation of the flight time.3 The frequency method uses a modulated laser source with a specific signal and the position can be calculated by applying the inverse Fourier transformation of the sensing fiber’s frequency response.4 The time-domain method is simpler than frequency-domain analysis but it requires a costly pulsed light source and higher-speed components.
Major parameters
Spatial resolution is a critical parameter in DTS. It is defined by the capability of resolving distance and determined by the pulse width or the maximum modulation frequency of the light source. Spatial resolution of 1 m is obtained using 10 ns pulses or 100 MHz modulation frequency. Typical spatial-resolution values range from under one to several meters.
In DTS, temperature resolution is defined as the ability to resolve the temperature reading. It is determined by the combination of measurement time and measurement distance (see Fig. 2). Raman DTS usually needs a long measurement time (from a few seconds to several hours depending on the application) because of the nature of the small scattering light intensity. Temperature resolution is usually specified for the worst value (at the maximum distance) and it ranges from less than 0.1°C up to a few degrees. The maximum measurement distance, which guarantees the specified temperature resolution, will range from a few kilometers to more than 15 km, with a resolution of 1°C for typical applications.
There is a common misunderstanding that higher (laser) power can cover longer distances. But this is true only for power under stimulated Raman conditions; otherwise the nonlinear phenomenon generates temperature error.
Practical challenges
Equation 1 shows the advantages of the DTS system (independent of the laser power, the launch condition, and the fiber type). But, with common attenuation, intensity profiles differ in both bands because of the wavelength difference in Stokes and anti-Stokes. Also, the attenuation difference is a nonlinear function of temperature. In addition, more temperature errors are expected for longer lengths in a higher-temperature environment. An example is the attenuation increase in sensing fiber induced by hydrogen gas ingression in oil wells for extended periods. To cancel the variations in attenuation, the double-end (DE) method, which deploys two sensing fibers side by side, has been applied, even though the half-length of sensing fiber is sacrificed. There is also an assumption that both fibers experience identical temperature.
The ideal solution for dealing with attenuation drift is to use the same wavelengths of Stokes and anti-Stokes spectra. But this concept is impossible to implement with a single light source unless a tunable laser is used. To date, either the size or the cost of the laser has been a major obstacle for a practical realization. A more practical and cost-effective method is to use a dual-source scheme, a secondary source whose Rayleigh or Stokes band is identical or similar to the anti-Stokes band of the primary.
In this self-calibrating scheme, two laser sources, a primary (1064 nm) and a secondary (980 nm), are connected alternatively to the reference and sensing fiber by a 1 × 2 optical switch (see Fig. 3). The attenuation profile of the anti-Stokes band of the primary source is precisely corrected by the Stokes profile of the secondary source because their bands are almost identical (see table). Also, the temperature-dependent attenuations between two bands can be handled effectively.
The 980 nm semiconductor lasers chosen as the secondary source are commonly used as a pumping source for the high-power fiber lasers. Their compactness, lower cost, and high power qualifies them as ideal candidates for the self-calibrating method.
The performance of the self-calibration scheme has been proved with a sensing fiber consisting of two sections-1.5 km of normal fiber exposed at room temperature and 700 m of severely hydrogen-darkened fiber exposed at under 40°C. The attenuation of the darkened fiber is four to six times higher than normal fiber. As a result, with normal operation temperature error occurs in the section of darkened fiber, but self-calibrated operation provides the correct temperature profile (see Fig. 3, bottom).
In addition to accurate temperature monitoring, the extended monitoring period of deployed fiber (increased sensing lifespan) will be another important benefit of newly introduced self-calibrating DTS.
Application areas
Raman DTS can provide advanced warning of anomalous and local temperature events, which would allow preventive action and planned maintenance, as well as the optimization of processes. Specific industrial applications include oil and gas wells and reservoirs, power cables, pipelines, storage tanks, process vessels, environmental and geothermal, fire detection, concrete curing of large structures, and offshore facilities.
ACKNOWLEDGMENTS
SensorTrans’s Kwang Suh Sr., optics engineer, and Mike Sanders, engineering manager also contributed to this article.
REFERENCES
1. E. Udd, Fiber Optic Sensors, John Wiley (1991).
2. J.P. Dakin et al, SPIE 566, 249 (1985).
3. U.S. patent 5113277.
4. U.S. Patent 7057714.
Tell us what you think about this article. Send an e-mail to [email protected].
CHUNG E. LEE is the corporate scientist for SensorTran, 4401 Freidrich Lane, Suite 307, Austin TX 78744; e-mail: [email protected]; www.sensortran.com.