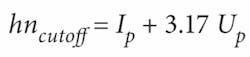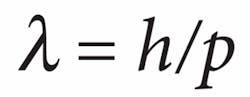Attosecond nonlinear optics open the door to coherent x-rays
Henry C. Kapteyn, Oren Cohen, Xiaoshi Zhang, Amy Lytle, and Margaret M. Murnane
Next year marks the fiftieth anniversary of the paper in which Arthur Schawlow and Charles Townes first proposed the laser. In the 1958 paper, those researchers presented calculations demonstrating the basic physical feasibility of the laser, a direct extension of concepts first demonstrated in the microwave region of the spectrum with the maser. Two years later, Theodore Maiman demonstrated the first laser.
Given this history, it was natural for researchers to look at the possibility of creating a laser in the x-ray region of the spectrum. The first proposals for soft-x‑ray lasers appeared in the late 1960s; however, actually making such a laser work is very difficult. The basic physics of the laser process dictate that the energy required to implement a laser scales roughly as λ-4-that is, a laser at 10× shorter wavelength requires on the order of 10,000× the input power. Thus, the first such lasers, implemented in the 1980s, used the building-size NOVA fusion laser at Lawrence Livermore National Laboratory (Livermore, CA) as a power source. Since then, considerable progress has been made in downscaling the laser needed as the power source. Researchers at Colorado State University (Fort Collins, CO), for example, have implemented lasers at wavelengths as short as 10 nm using a laboratory-size (about 1 J) picosecond laser.
What are the prospects for hard-x-ray lasers, with wavelengths shorter than 1 nm? Coherent light can be generated at these short wavelengths using synchrotron laser sources, or the new free-electron lasers such as the (under construction) Linac Coherent Light Source (Menlo Park, CA). However, again these are very large-scale light sources, of which only a few will ever be built.
Much of the impact of the laser has been as a practical device to use in applications such as compact-disc players and fiber-optic communications. Unfortunately, given the energy requirements, small-scale coherent x-ray sources would seem to be more a topic of science fiction than near-term reality.
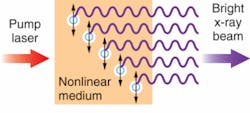
Or are they? Surprisingly, during the past decade, an alternative approach for generating coherent x-rays has made rapid progress. For the first time, there is a reasonable prospect that tabletop coherent x-ray sources, even in the hard-x-ray region of the spectrum, may be possible. This new technology relies on a new basic understanding of the physics of laser-atom interactions that was totally unanticipated when first seen in experiments in the late 1980s. It involves an understanding of atomic dynamics on the fastest (attosecond) time scales relevant to atomic and molecular (that is, non-nuclear) processes.
Extreme nonlinear optics
The field of nonlinear optics has a history almost as long as the laser itself. Indeed, the first experiment in nonlinear optics, by Peter Franken at the University of Arizona (Tucson, AZ), was done using a ruby laser scarcely a year after the laser’s first demonstration. In nonlinear optics, bright light from a laser is incident on a material. The oscillating electric field of the laser causes the electrons in the material to oscillate. However, if the laser is strong enough, the electrons (normally bound to atoms in the material) begin to reach the limits of their bonding. In this case, their motion is no longer sinusoidal, but distorted-consisting of the fundamental as well as a harmonic. This effect is analogous to playing an electric guitar very loudly-the acoustic distortion corresponds to higher harmonics of the fundamental tone.
Harmonic generation has found an increasing role in lasers as a way of increasing the wall-plug efficiency of lasers operating in the visible and UV. Argon-ion lasers, for example, have been made obsolete by a new generation of neodymium-based lasers that operate in the infrared and use nonlinear crystals to efficiently upshift the laser into the green by frequency doubling.
Why not push the same techniques to an extreme for generating x-rays? Unfortunately, difficulties become immediately obvious. In conventional nonlinear optics transparent crystals are used for frequency conversion to phase-match the process. Unfortunately, crystals are not transparent to wavelengths shorter than about 200 nm. Thus, conversion to very short wavelengths can only be done in a gas.
Fortunately, when a very intense, ultrashort-pulse laser is focused into a gas, very high-order harmonics are observed. The first experiments, in the late 1980s, immediately demonstrated something remarkable about these harmonics. In conventional nonlinear optics, each successively higher harmonic order becomes successively dimmer, as would be expected for a perturbative nonlinear process. In contrast, in high-order harmonic generation, there exists a “plateau”-a series of harmonic orders that all have comparable conversion efficiency.
This plateau was first explained about 15 years ago as a consequence of the fact that the high-order harmonic generation (HHG) is intimately associated with ionization of the atoms in the gas. A “three-step” model was developed that was shown to predict a similar plateau (see Fig. 1). An atom subjected to a strong laser field will ionize; once this happens, it begins to oscillate violently in the field of the laser. After ionization, some of these electrons return to the vicinity of their parent ion, with high energy and faster than an optical cycle (that is, in about 1 fs). A simple classical picture of this process yields a remarkably accurate expression for the “cutoff” of the plateau in HHG:
where Up is the “ponderomotive potential,” or the time-averaged oscillation energy of the electron at the laser intensity when the electron ionizes, and Ip is the ionization potential of the electron. This cutoff photon energy corresponds to photon energies of tens of electron volts up to even greater than 1 keV. This is a direct result of the very favorable scaling of HHG compared with x-ray lasers-the cutoff photon energy is linearly proportional to the intensity of the incident laser. Furthermore, the required laser intensities of about 1015 to 1016 W/cm2 are readily accessible with millijoule-energy pulses from a tabletop femtosecond laser system.
Finally, it is interesting to note that this “three-step” model is very much a coherent version of the very first x-ray generation process-the Roentgen x-ray tube. In this device, electrons are accelerated using a high-voltage power supply, and x-rays are generated when these electrons slam into a target. High-order harmonic generation is the coherent version of this process-a coherent laser field generates and then accelerates electrons, and they collide with their parent ions in a predictable way. Thus, the HHG emission retains the coherence of the incident laser, emerging from the gas as a collimated beam.
The phase-matching problem
The first experiments in HHG were very analogous to Franken’s first demonstration of second-harmonic generation-the process was clearly observed, but the conversion from laser light to shorter wavelengths was very inefficient. The second major enabling breakthrough for second-harmonic generation was the demonstration of birefringent phase matching. To generate harmonic light efficiently in a long crystal, one must match the propagation speed (more precisely, the phase velocity) of the two waves (see Fig. 2). In this way, the signal generated by the nonlinear process adds constructively over the entire interaction length. The constructive addition of signal electric fields results in an intensity that builds quadratically with propagation distance.In a crystal, this propagation speed is adjusted through a combination of polarization and birefringence of the nonlinear medium; that is, the physical structure of the medium is used to modify the speed of the waves. Unfortunately, HHG must use a gas as the nonlinear medium-if one tried to drive a crystal at ionizing intensities, the free electrons ionized would rapidly create a mirror that reflects the incident light, and subsequently the material would be destroyed. Thus, to accomplish phase-matched conversion in this case of “extreme” nonlinear optics, we need to develop a completely new toolbox of techniques for phase matching.
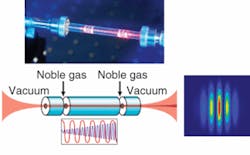
The first progress in this area was made in the late 1990s through the use of hollow-waveguide geometries for frequency conversion. The concept of using guided-wave propagation of light for phase-matched nonlinear optics has been used in conventional nonlinear optics, but it is especially useful for HHG. Moreover, one can use a structure surrounding the nonlinear medium to modify the propagation of the driving laser. A hollow waveguide containing a gas can guide ultrafast pulses intense enough to generate HHG without damaging the waveguide. The waveguide creates a plane-wave propagation, and the effects of the gas, the waveguide, and the (time-varying) ionization free electrons can be balanced to phase-match the frequency conversion. (see Fig. 3).X-ray photonics
However, this type of phase matching has a serious limitation: ionization of the medium. As the intense laser ionizes the medium, a high-enough free-electron density becomes so dispersive—speeding-up the phase velocity of the driving laser in comparison to the short-wavelength light-that there is no way to obtain good phase matching. While very short-duration pulses can reduce ionization, even for helium (the most difficult-to-ionize medium) phase-matched conversion is possible for photons with energy up to about 150 eV.
Solving the phase-matching problem for high-energy x-ray photons remained a problem for more than five years, because this problem is so different from phase matching in conventional nonlinear optics—the medium is isotropic and the phase-matching conditions are changing dynamically.
However, the first progress in this area was made in 2003, with the demonstration of quasi-phase-matching (QPM) of high-harmonic generation using periodically modulated waveguides. Quasi-phase-matching is a concept from conventional nonlinear optics. In QPM, the nonlinear response of a medium is modulated with a period that corresponds to what the coherence length would have been in a uniform medium. This modulation is accomplished, for example, in periodically poled nonlinear materials such as periodically poled lithium niobate, when periodically reorienting the nonlinear crystal can make the nonlinear signal flip sign just as the signal and the pump light slip in phase by one-half wave. In this way, the signal continues to build throughout the medium-despite a phase-velocity mismatch.
To implement QPM for HHG, rather than change the structure of the nonlinear medium we can change the structure surrounding the medium in a periodic way. By virtue of the “cutoff rule,” one can see that for the 99th harmonic order, for example, modulating the cutoff by one harmonic order (that is, turning the cutoff harmonic on and off) can be accomplished using only a approximately 1% modulation in intensity of the driving laser. This modulation can be induced by varying the diameter of the waveguide.
This technique works very well to enhance the x-ray flux by over an order of magnitude. However, it also has its limitations-as the modulation period becomes shorter than the waveguide diameter, the intensity modulations rapidly diminish. As a result, the photon energies that can be phase-matched are still limited.
Attosecond science for x-ray photonics
Fortunately, there is a way forward. In the preceding section, the recollision physics of HHG was essentially described as a classical-physics picture—a “point” electron driven by a laser. However, the electron is a quantum particle with a wave function. In the more-accurate quantum picture, the HHG process corresponds to a portion of the electron wavefunction tunneling out of the atom, evolving outside the atom in response to the laser field, and then scattering from the atomic core (see Fig. 1, bottom). A semiclassical picture of HHG simply keeps track of the de Broglie wavelength of the electron:
as the electron makes its way along its “boomerang” path. Remarkably, the total phase accumulated by the electron during this attosecond-time-scale trajectory is quite large—on the order of one radian of phase per harmonic order (that is, the 99th harmonic would be emitted by an electron whose wave function evolved through about 100 radians—dozens of cycles—before recolliding!). Because the high-energy photon is emitted in the recollision event, the phase of the emitted x-ray is shifted with respect to the phase of the driving laser.
This “intrinsic phase” is a type of physics that is completely absent in conventional nonlinear processes such as second-harmonic generation—which complicates the high-harmonic process, but also makes it possible to manipulate it.
Crystals made of light
The high-harmonic nonlinearity is unique as a purely electronic nonlinear-optical response that has a finite (although extremely fast) response time. This leads to the question: Can the intrinsic phase be used to phase-match the conversion process? In fact, the answer is yes. Variations in the laser intensity shift the exact timing of the x-ray emission, and this shift can keep the emission in phase as the beam propagates. Therefore, a second laser pulse can be used to perturb the trajectory of the electron. The intrinsic phase of the electron is sensitive to the electric-field strength applied to the atom, which is just the vector sum of any and all incident waves. In particular, the use of a pulse traveling in the opposite direction is particularly useful because it can be used for spatially selective manipulation.
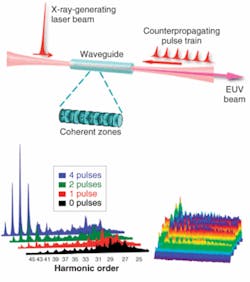
This idea was actually first suggested more than a decade ago. Experiments by the Peatross group at Brigham Young University (Provo, UT) had shown that a second beam could be used to suppress high-harmonic emission. In very recent work, we have shown that, by combining the use of a waveguide geometry with a “train” of counterpropagating pulses, quasi-phase-matching with very dramatic (greater than 500×) enhancements of x-ray flux can be demonstrated (see Fig. 4). Using a train of relatively weak counterpropagating pulses of picosecond duration, we enhanced the high-order harmonic emission by successively adding one, then two, three, and finally four pulses. Separate measurements using this same setup directly measure the coherence length for the conversion as a function of harmonic order, and confirm that the harmonic order most enhanced by the counterpropagating pulse train is the one in which the coherence length matches the spacing between the pulses. Essentially, the train of light pulses forms a “crystal structure” made of light that makes it possible to phase-match the high-harmonic process.What about hard x-rays?
The physics of HHG is certainly one of the great success stories of nonlinear optics in the past 20 years. Several applications have been demonstrated in the extreme-UV and soft-x-ray regions of the spectrum, including nanoimaging, materials dynamics, and new ultrasensitive attosecond x-ray spectroscopies and radiation chemistry.
Just how far can we go? Is it possible to generate bright coherent hard x-rays, which could revolutionize crystallography, biological, materials, and medical imaging? The answer is yes, in theory-phase-matched conversion to very high kilo-electron-volt photon energies is possible, guaranteeing more exciting advances in extreme nonlinear optics.
REFERENCES
1. H. Kapteyn et al., Physics Today, p. 39 (March 2005).
2. R. Bartels et al., Science 297, 376 (2002).
3. X. Zhang et al., Nature Physics (April 2007).
HENRY C. KAPTEYN, OREN COHEN, XIAOSHI ZHANG, AMY LYTLE, AND MARGARET M. MURNANE are researchers at JILA and the Department of Physics at University of Colorado, and NIST and the National Science Foundation Engineering Research Center in Extreme Ultraviolet Science and Technology; University of Colorado, Boulder, CO 80309-0440; e-mail: [email protected].
The optics behind the science
Ultrafast pulses are a scientist’s dream; their brevity allows snapshots of atomic and biological processes, while their high peak power provides new ways to study altered states of matter. In this Optoelectronics World supplement, researchers at JILA highlight developments in extreme-UV nonlinear optics that may result in hard-x-ray lasers; Steve Kane and Bruno Touzet of Horiba Jobin Yvon describe a grism-based pulse compressor that can compensate for glass paths of hundreds of meters; and Marcos Dantus and colleagues at Michigan State University discuss their noninterferometric technique to calibrate and remove pulse distortions.
John Wallace, Senior Editor