PLASMONICS: Small gain yields great control

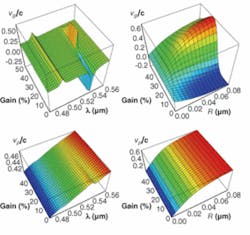
Optical gain in subwavelength waveguides is generally used for compensating losses. But it may also enable control of dispersion and propagation of electromagnetic pulses at the nanoscale, perhaps even leading to a nanoscale optical transistor.

Plasmonics allows light to be confined to nanoscale dimensions where a typical waveguide cross section would be much smaller than the wavelength, according to Viktor Podolskiy, assistant professor of physics at Oregon State University (Corvallis, OR). But the plasmonic materials that confine the propagation of radiation, exceeding the diffraction limit within nanowaveguides, are often limited in effectiveness by propagation losses inherent in the plasmonic material. A major thrust of plasmonic research involves overcoming propagation losses by adding gain using either bulk-scale lasers, very high-quality gain materials, or both, Podolskiy said. His research team, however, has been looking at the effects on plasmonics of levels of gain and material quality much lower than what would be required to compensate losses.

Gain materials themselves have dispersion, which has been used in experiments involving slow and fast light, Podolskiy said. At the macroscopic scale, material dispersion comes into play; at the nanoscale, however, the shape of the material and material dispersion come into play. In studying the use of gain to control the dispersive properties of active nanoscale waveguides, the researchers observed that even relatively weak material gain, which is unable to compensate losses, is capable of producing large variations of the group velocity, enabling generation of slow and fast light on the nanoscale. The interplay between material- and geometry-induced modal dispersion appears to be the factor that enables such strong group-velocity modulation even when the material dispersion is relatively weak.

“It turns out that to moderate group velocity, only a slight change in material dispersion is required,” Podolskiy said. “So you don’t need high-quality gain materials; moderate quality is sufficient.”

His research team has developed and demonstrated a mathematical model for modulating group velocity of light from slow to superluminal, in excess of the diffraction limit, in subwavelength waveguides (see figure).¹ Podolskiy described the basic system as a nonhomogeneous waveguide structure. “With nondispersive materials, only the geometric effects come into play. If you decrease size, the group velocity goes to infinity. With dispersion, the group velocity goes to zero. That is how you moderate group velocity with material dispersion or geometry by just changing the gain level a little bit.”

Their mathematical model can be directly applied to arbitrary waveguide geometries, including planar, square, circular, and oval systems. It can be applied to plasmonic, coaxial, and volume waveguide modes and different sets of materials (polar dielectrics, semiconductors, quantum wells, quantum dots) scaled for UV, optical, IR, terahertz, and microwave spectral regions.

Photonic funnels and compressors

Because the group velocity can be independently controlled by either material dispersion or waveguide radius, it should be possible to construct a tapered plasmonic fiber in which plasmonic packets would travel faster than light speed at larger radii and slower than light speed toward the small-radius apex; also referred to as switching from a photonic funnel to a photonic compressor, said Podolskiy.

“In a funnel, when you decrease the radius, the water accelerates because of mass conservation,” Podolskiy said. “There is no mass conservation in photons. But with no dispersion as waveguide size decreases, group velocity increases, which is kind of analogous to a funnel. With dispersion, however, with a decrease in size, group and phase velocity go to zero upon reaching a critical radius. So this is how these factors can switch between funnel and compressor functions.”

One potential application of this mathematical model is in pulse synchronization. “When pulses are propagating in different waveguides, you can synchronize them to compensate for dispersion,” Podolskiy said. “You can also control gain optically. When there is a control pulse you have gain, and when there is none you have no gain. Also, if you have gain, the waveguide becomes transparent. But with no gain, there is no signal (it is absorbed). So you could conceivably make an optical transistor on the nanoscale.”

So far, the demonstration of this concept has been through theory and numerical modeling, but Podolskiy’s group has begun collaborating with another to experimentally test the model for dispersion management in plasmonic waveguides.