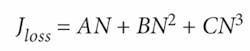Software enables optimized epi structure in a single wafer growth
Jerome Moloney
Semiconductor lasers and optical amplifiers are pervasive components in modern technology spanning a huge applications space. And semiconductor-wafer growth can now produce heterostructures of very high quality with stoichiometrically controlled growth of individual monolayers. However, even if the perfect crystalline material could be grown, one would be no closer to designing a targeted semiconductor optical amplifier (SOA) or laser.
The practice in semiconductor materials growth has typically involved an estimation of the absorption-band edge via simple band-structure calculations followed by a costly and inefficient series of growth, packaging, and regrowth cycles accumulated over the typical 15 to 20 years operating life of a company. Our research over 15 years recently addressed this problem by demonstrating the ability to predict a semiconductor-laser input-output (L-I) characteristic based on fundamental principles without using adjustable fit parameters.
A key enabler in this accomplishment was the solution just a few years ago of the semiconductor lineshape problem. The spectral lineshape at low external light illumination intensities yields photoluminescence (PL) spectra that provide invaluable feedback to the semiconductor-wafer grower on growth accuracy and quality. The inverted semiconductor gain lineshape tells us where the laser will optimally lase (peak gain) and the spectral bandwidth available for light amplification, in an SOA, for example. Many attempts had been made over the years to resolve the lineshape problem, with little success until 1996.1 The key observation was that carrier-carrier and carrier-phonon (lattice) many-body interactions occurring on tens to hundreds of femtosecond timescale, cannot be treated as irreversible decays to a thermal heat bath-instead, strong correlations exist within the electron-hole plasma and they have to be resolved by solving a quantum Boltzmann scattering problem. Once this was realized, the calculated lineshapes agreed quantitatively with measured spectra in both location of the spectral peaks and shape of the spectrum.
To demonstrate the failure of even the best conventional approach, we show computed gain spectra (blue lines) where we carry out many-body calculations using the semiconductor optical Bloch equations but attempt to parameterize the scattering processes in terms of the familiar optical Bloch model T1 and T2 relaxation times (see figure, left). Experimental gain spectra are shown with red dots at different excitation levels. The comparison clearly demonstrates that gain peak magnitude, location, and lineshape cannot be made to agree with the experimental data and moreover, the gain at longer wavelengths (in the semiconductor bandgap) shows absorption-a clearly nonphysical behavior. The same experimentally measured gain spectra lie on top of the full calculations when we include Coulomb many-body correlations within the electron-hole plasma and the carrier-phonon coupling by solving the relevant quantum Bolzmann equations (see figure, right).
null
Quantitative predictions
The message here is that we can now quantitatively predict gain-and similarly also PL- for material systems encompassing the III-V and II-VI material systems without having to resort to using phenomenological fit parameters. The critical inputs needed to get going are generic bandstructure parameters and band offsets, which are well known for many material systems such as gallium arsenide/indium gallium arsenide/aluminum gallium arsenide (GaAs/InGaAs/AlGaAs) spanning emission wavelengths from 800 nm to 1.2 µm, and indium gallium phosphide arsenide/indium phosphide (InGaPAs/InP) spanning the important telecommunications range from 1.3 to 1.5 µm. Even though some input parameters are less well known, we were recently able to extend our microscopic calculations successfully to technologically important visible nitride (GaN, InGaN) and mid-IR antimonide (GaSb, InGaSb) materials.
With the lineshape problem well in hand, the remaining elusive semiconductor optical properties needed before we could close the loop and predict an end laser performance were radiative (spontaneous) and nonradiative (defect and Auger) losses. To quantitatively compute spontaneous emission losses, we needed to solve an extended many-body problem in which it is necessary to quantize the light field.2 Auger losses add a further challenge to the theory as these involve transitions between states in several bands spanning a large fraction of the Brillouin zone. We managed to numerically handle these effects in 2005 with the first quantitative comparison with measured Auger rates.3
The microscopic mechanisms of the basic radiative and nonradiative loss processes consist of nonradiative defect recombination losses varying linearly with carrier density N, spontaneous radiative losses often assumed to depend on the carrier density squared (an electron and hole are required to emit a photon) and nonradiative Auger losses often taken as proportional to carrier density cubed. Other loss mechanisms may be operative, as in shallow QWs in the presence of dopant fields where carriers can tunnel out of the confinement region. The generally accepted expression for the current loss is:
Generally, in high-quality crystal growth, defect recombination tends not to be a player. The phenomenological rates in the above equation are only valid at very low carrier densities (uninverted semiconductor) where the carriers are in Boltzmann distributions. However, in every inverted (lasing) semiconductor material, the carriers are in Fermi distributions. The interactions are dominated by many-body effects. Our experimentally validated calculations of both spontaneous and Auger losses verified that the above simple power-law carrier dependencies are incorrect. These recombination processes fundamentally influence many operational characteristics, static and dynamic, of a semiconductor laser or amplifier. Therefore, to be scientifically consistent we should extrapolate the spontaneous and Auger rates from their low density values to the clamped laser densities.
Once the gain and recombination losses are tied down, we are in a position to close the loop and predict the performance of a real laser. This was done recently for a 1.3 µm InGaPAs low-power laser structure-the only measured inputs needed were the intrinsic absorption/scattering losses determined from cut-back experiments.4 The predicted laser input-output characteristics were computed prior to the experimental measurement and the experimental data lay on the predicted curves when a slight temperature elevation in the active region was allowed for.
As semiconductor active and passive materials migrate into maturing nanotechnology applications, the need for such a rigorous quantum design approach will be even more critical. Nonlinear Control Strategies of Tucson has won a Phase II STTR award from the U.S Air Force to provide the enabling commercial software to achieve this end; an initial product has been developed and is projected to be available early in 2008.
Editors note: A more detailed discussion of this research can be viewed at www.laserfocusworld.com/articles/294844.
REFERENCES
1. S. Hughes, A. Knorr, S.W. Koch, R. Binder, R.A. Indik, J.V. Moloney, Solid State Communications100, 555 (1996).
2. M. Kira, S.W. Koch, Progress in Quantum Electronics 30, 155 (2006).
3. J. Hader, J.V. Moloney, S.W. Koch, IEEE J. Quantum Electronics41(10) 1217 (2005).
4. J. Hader, J.V. Moloney, L. Fan, M. Fallahi, S.W. Koch, Optics Lett.31(22) 3300 (November 2006).
JEROME MOLONEY is the president of Nonlinear Control Strategies, 5669 N Oracle Rd., Suite 2201, Tucson, AZ 87504; e-mail: [email protected]; www.nlcstr.com.