PHOTONIC FRONTIERS: QUANTUM COMPUTING - Quantum computing poses challenges
If you believe the press releases, quantum computing is the next big thing, soon to vastly surpass the capacity of today’s supercomputers. There’s no doubt it’s a hot topic. A search of the Quantum Physics section at Cornell University’s arXiv.org for papers with “quantum” and “computing” in the title yields more than a thousand hits. Yet probe a bit and you find that quantum computing offers tremendous processing power only for a very limited range of applications.
Both the nature of these applications and the conceptual challenges posed by quantum computing drive many research programs. The most compelling potential application is the factoring of gigantic numbers, crucial because current data encryption techniques depend on factoring being difficult. Conventional computers attack the problem by brute force and would need billions of years to crack a 2048-bit code that-in theory-a big enough quantum computer could factor in an hour. Concern over this possibility drives research funding. Other interesting but less critical potential applications are searching vast databases and modeling the complexities of quantum mechanics.
Nobody says quantum computing will be easy, or that it could replace today’s binary computers for ordinary tasks, from balancing your checkbook to forecasting the weather. Yet the field is fertile with ideas, and optics is one of many technologies being investigated.
Quantum superposition
Conventional digital electronic computing operates on entities such as logic gates that have two possible states, 0 and 1. Quantum computing instead manipulates quantum-mechanical bits or “qubits,” which, as quantum-mechanical entities, are superpositions of states. One example is photon polarization. Until it is measured, the photon polarization is a superposition of two states, such as linear horizontal and vertical polarizations, so a quantum computer that operates on an unmeasured photon interacts with a superposition of the two states.
The real power of quantum computing comes from operating on multiple qubits. You can see the difference for three-bit systems. Three classical bits can have eight possible combinations of zeros and ones, binary codes representing the numbers 0 to 7. In contrast, three qubits exist in a superposition of those eight possible binary states, described by a wavefunction:The amplitude of each state is a complex number of the form x+iy. The probability of the three-qubit system being in a particular state is the absolute value of the amplitude squared, |(x+iy)2|. N qubits can represent 2quantum states.
Quantum computing operates on an input wavefunction of the qubits according to an algorithm that alters the amplitudes of the quantum states to increase the probability of a particular state. Repeating the procedure can further increase the probability of that state until it is close to one. However, the qubit remains a superposition of states until a detector measures its properties, collapsing the probabilistic wavefunction to a known state (see Fig. 1).
Advantages
Richard Feynman first realized the potential of quantum computing a quarter-century ago and proposed using it to model the evolution of quantum-mechanical systems.1 Modern digital computers still can’t handle such models, but a large enough quantum computer should be able to simulate systems of interest, says Jeffrey Shapiro, director of the MIT research laboratory of electronics.
The idea that stimulated serious interest from funding agencies was a 1994 demonstration by Peter Shor, now at the Massachusetts Institute of Technology (MIT; Cambridge, MA), that a quantum computer could determine the periodicity of a sequence of numbers. Knowing that periodicity reveals the factors of the number.2 Shor developed the first quantum-mechanical algorithm, and showed that it could quickly factor immense numbers-potentially cracking widely used digital encryption technology. The potential improvement over conventional computers is dramatic. Karl Berggren of MIT calculates that a quantum computer operating at 100 MHz could factor a 2048-digit binary number in about an hour-compared to 1015 hours, longer than the life of the universe, for a future supercomputer performing 1015 operations a second (see Fig. 2).3In 1996, Lov Grover of Bell Labs (Murray Hill, NJ) developed a quantum-computing algorithm for finding one item in an unstructured database. His approach uses a series of quantum-mechanical operations to increase the amplitude of the desired item so only N1/2 steps are needed to search a list of N items, compared to N steps for a conventional search.4
Challenges and approaches
There is no shortage of ideas for how to make a quantum computer, but the requirements are extremely challenging. Quantum information is fragile because quantum states can change easily and can’t be observed without destroying them. Qubits must interact with each other, and maintain their quantum state long enough to perform computations. Quantum measurements are challenging, and they destroy the data being read by collapsing the quantum wavefunction into a single observed state. The system must be fault-tolerant because quantum states are probabilities.
A key challenge is to make multiple qubits that meet these requirements and can interact with each other. So far, liquid-phase nuclear magnetic resonance (NMR) has generated the most qubits, but Shapiro says that approach is limited to about 10 qubits. Solid-state NMR is promising, but not well developed. Trapped ions, atoms, and electrons also are promising candidates for qubits. Superconducting devices can draw on earlier work in superconducting electronics, but their quantum-state lifetimes have been limited.
Photons have their own attractions. They tend to maintain their quantum properties such as polarization because they interact weakly with their environment. However, their weak interaction with each other complicates quantum computation, and because they continually move at the speed of light they are hard to store.
In 2001, Emmanuel Knill and colleagues at the Los Alamos National Laboratory (Los Alamos, NM) showed that in theory an optical quantum computer consisting of single-photon sources, linear optical elements such as beamsplitters and waveplates, and photon detectors could in principle be more efficient than a classical computer.5 More recent work has relaxed requirements for optical perfection, and reduced the number of physical operations needed for each logical operation.6
“We have a problem in that single-photon (one-qubit) operations are easy, but two-photon operations are extremely hard,” says Pieter Kok of Oxford University (Oxford, England). One trick to overcome that limitation is to entangle the photons first, then perform computations by measuring the polarizations of single photons, a technique called “measurement-based quantum computing.” The technique has its own difficulties; the photons want to move away at the speed of light, so must be trapped in a photon memory. “This is a shame, because it will introduce a lot of noise into the computation,” says Kok.
Kok and Sean Barrett, now at Imperial College (London, England), have come up with a new trick: instead of trying to trap the photon in a memory cell, they make the memory cell itself the qubit. “We then no longer have to couple the photon into it (extremely hard); we only have to get the photon out (still hard, but much less so),” Kok says. They entangle two memory cells by sending photons emitted from both cells through a 50-50 beamsplitter, which entangles them because it is no longer possible to tell which photon came from which source. Kok says their approach can also create large entangled states; their next challenge is to find the best physical approach to making memory cells.
An alternative approach developed by the National Institute of Informatics (Tokyo) and Hewlett-Packard Laboratories (Gifford, Bristol, England) combines communications with quantum computing so qubits do not interact directly. Instead, each interacts with a quantum “bus” or qubus, which transmits a coherent state between the two. Unlike the qubit, the coherent state on the qubus is a continuous variable, which interacts with each qubit. Controlled rotation of the qubus state in effect communicates quantum information between the qubits. “Our scheme is universal and works in any regime, including the limits of weak and strong nonlinearities,” the authors write.7
Outlook
In February a company called D-Wave Systems (Vancouver, BC, Canada) even demonstrated what it called the “world’s first commercial quantum computer.” But most researchers consider that claim premature.
A host of issues remain to be resolved. Many schemes require single photons, which are difficult to generate (see www.laserfocusworld.com/articles/257230) and which interact so weakly with each other that quantum computation is very inefficient. Random quantum fluctuations contribute to measurement errors. “A lot of work remains to be done before there are large-scale quantum computers,” Shapiro says.
Optics are only a small part of the picture, and old-timers will recall that a previous generation of “optical computing” research never met the high expectations of a generation ago. Yet, if the past is any guide, optical quantum computing may pay unexpected dividends, whether or not it fulfills today’s high hopes.
REFERENCES
1. R. Feynman, Int’l. J. Theoretical Physics 21, 467 (1982).
2. W. Peter Shor, Proc. the 35th Ann. Symp. on Foundations of Computer Science, Santa Fe, NM (Nov. 20-22, 1994); IEEE Computer Society Press, 124 (Arxiv.org:quant-ph/9508027).
3. K. Berggren, Proc. IEEE 92, 1630 (Oct 2004).
4. L. Grover, Phys. Rev. Lett.79(2), 325 (July 14, 1997). Arxiv.org:quant-ph/9706033.
5. E. Knill, R. Laflamme, and G. J.Milburn, Nature409, 46 (2001).
6. P. Kok et al., arXiv.org:quant-ph/0512071, v2, 14 (March 2006).
7. P. van Loock et al., Arxix.org:quant-ph/0701057, v1, 11 (January 2007).
About the Author
Jeff Hecht
Contributing Editor
Jeff Hecht is a regular contributing editor to Laser Focus World and has been covering the laser industry for 35 years. A prolific book author, Jeff's published works include “Understanding Fiber Optics,” “Understanding Lasers,” “The Laser Guidebook,” and “Beam Weapons: The Next Arms Race.” He also has written books on the histories of lasers and fiber optics, including “City of Light: The Story of Fiber Optics,” and “Beam: The Race to Make the Laser.” Find out more at jeffhecht.com.
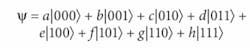
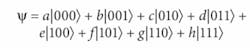
![FIGURE 2. In a comparison of time needed to factor binary numbers of various length using quantum and conventional computers, conventional computers are much faster for small numbers, but the required computing time increases rapidly with the number of digits. Quantum computers are slower for small numbers, but much faster for large ones [3]. FIGURE 2. In a comparison of time needed to factor binary numbers of various length using quantum and conventional computers, conventional computers are much faster for small numbers, but the required computing time increases rapidly with the number of digits. Quantum computers are slower for small numbers, but much faster for large ones [3].](https://img.laserfocusworld.com/files/base/ebm/lfw/image/2016/01/th_0707lfw_03f2.png?auto=format,compress&fit=max&q=45?w=250&width=250)
