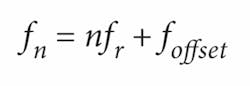PHOTONIC FRONTIERS: FREQUENCY COMBS - Frequency combs achieve extreme precision

Fourier transforms can offer a whole new perspective on physical phenomena. Transform a single femtosecond pulse from the time domain into the frequency domain, and you have a broadband continuum. But transform a modelocked train of femtosecond pulses into the frequency domain and you find something dramatically different. The repetitive pulses become an optical frequency comb, a set of very sharp and narrow frequency spikes uniformly spaced across the spectral bandwidth of the light source. The comb peaks are continuous-wave, extremely narrow, and separated by the pulse repetition rate (see Fig. 1).
Frequency combs were a striking concept, but reaching their full potential required a second exotic development: highly nonlinear photonic-crystal fibers that tightly confined broadband light and stretched its spectral width across a full octave in frequency. The combination of the two effects produced an amazing “single-laser self-calibrating frequency synthesizer” ideal for precision metrology and physical research, wrote John Hall of the National Institute of Standards and Technology (Boulder, CO) in 2001.1 Its octave bandwidth created three million uniformly spaced frequencies, and brought about a new generation of precision measurement. For their work in advancing the frequency comb, Hall and Theodor Hänsch of the Max Planck Institute for Quantum Optics (Garching, Germany) won the 2005 Nobel Prize in Physics.
The importance of frequency
Optical physicists and engineers tend to think of light in terms of wavelength, but wavelength is a difficult quantity to measure. Frequency can be measured more precisely, particularly in the radio and microwave spectrum. Direct measurements of higher frequencies were based on chains of harmonic generation, with the high-order harmonics phase-locked to higher-frequency lines.
In 1995 a series of painstaking experiments reached visible wavelengths. A team at the German Federal Physical-Technical Institute (Physikalish-Technische Bundesanstalt; Braunschweig, Germany) created a frequency chain from the cesium atomic clock at 9.2 GHz to the calcium-stabilized optical-frequency standard at 657 nm (456 THz).2 It was an elegant experiment, but it required three large laboratories full of equipment and could measure only one optical frequency at a time.
Frequency-comb generation overcomes both limitations. Although femtosecond modelocked lasers are not exactly simple, they are much less complex than a traditional frequency-chain system. They automatically generate multiple frequencies that are precisely spaced at intervals of the modelocking frequency. The higher the modelocking frequency, the wider the spacing of comb lines, which in general makes measurements easier.
The frequency fn of each mode is written as
where n is the mode number, fr is the repetition rate (the spacing between modes), and foffset is an offset frequency at a frequency between 0 and the repetition rate (shown in Fig. 1). The offset is proportional to the phase shift between the wave envelopes in successive pulses, which arises because the carrier wave moves at the phase velocity of the pulses but the envelope moves at the group velocity.
The constant spacing between the frequency peaks makes the comb a natural optical ruler. It is straightforward to measure the difference between two stable optical frequencies by beating both against separate lines of the comb to obtain microwave difference frequencies, then counting the number of comb peaks separating the two stable frequencies.The widths of frequency combs from femtosecond lasers are limited by the gain bandwidth of laser materials such as titanium sapphire, but the bandwidth can be stretched by nonlinear materials. Hänsch recognized the potential to extend frequency combs across a broader range when he saw a white-light continuum produced by passing femtosecond pulses through a material with high third-order nonlinear susceptibility.3 Experiments confirmed that the white-light continuum had the needed coherence.
Another key experiment came in mid-1999, when Bell Labs generated a white-light continuum spanning a whole octave in frequency by passing femtosecond pulses through a highly nonlinear photonic-crystal fiber. Those results sent Hänsch and Hall on a quest for samples of the special fiber, but Bell wouldn’t loan them out. In his Nobel lecture, Hall recalled, “Lengthy appeals for scientific collaboration with the fiber owners’ organization ultimately became irrelevant due to the miraculous appearance in JILA of a sample of this Magic Fiber.”4 Hänsch got his own sample from Philip Russell’s group at the University of Bath (Bath, England). The results proved as good as they had hoped (see Fig. 2).An octave-wide frequency comb offers a critical advantage. Light at the low-frequency end can be frequency-doubled and mixed with light at the blue end of the comb, producing a collective beat note at exactly the offset frequency, which otherwise can be difficult to measure accurately (see Fig. 3).
Once the offset frequency is known, absolute frequency measurements are possible. An unknown frequency can be measured by first using a wavelength meter to determine the mode number n of the closest comb line, then beating the unknown frequency with the comb line to count the frequency difference between the two. Adding the offset frequency gives the absolute frequency. Alternatively, one line in a frequency comb can be locked to a sharp optical reference line. Combining that known frequency with the pulse repetition rate (the comb spacing) calibrates the entire comb with the accuracy of the frequency standard, allowing measurements across a wide range.
Other developments increased the power of the technique. Changing the power of the pulse circulating in the laser can tune the offset frequency if modelocking is done with a Kerr lens, so a frequency comb can synthesize optical frequencies.
A revolution in measurement
Optical frequency combs greatly simplify optical-frequency measurements and greatly improve their precision. A frequency comb can be the foundation for an optical-frequency synthesizer, in which the comb controls the output of a broadly tunable continuous-wave laser.5 Combs are stable and can measure frequencies with incredible precision. One experiment confirmed that the second harmonic of an Nd:YAG laser is exactly a factor of two higher than the fundamental with an uncertainty of only six parts in 1021.6 This year at CLEO (Baltimore, MD) William C. Swann of NIST in Boulder, CO, reported high and low lines in a frequency comb remain stable to within six parts in 1017. “The performance of these lasers right now is absolutely astonishing,” says Brian Kolner of the University of California at Davis (Davis, CA), who is studying fundamental limits that quantum noise imposes on linewidth of a single comb line.
So far, many applications have been in fundamental physics. One intriguing example is testing the controversial idea that physical constants change over time. Astronomical tests can peer back into deep time in the distant universe, but they are subject to systematic errors. The extreme precision of frequency-comb measurements have better-quantified upper limits. Recent experiments have set an upper limit on current variability of the fine-structure constant of (-0.3 ± 2.0) × 10-15 per year.7, 8 Other measurements can test the accuracy of fundamental theories such as quantum electrodynamics, says David Weiss of Pennsylvania State University (University Park, PA). The extreme stability of frequency combs will allow spectroscopists to probe atomic transitions in the visible and infrared that were too narrow to study with conventional sources, says Kolner.
A long-term thrust is to develop optical clocks to replace current microwave standards. For the past 40 years, the second has been defined as 9,192,631,770 oscillations on a hyperfine transition of the ground state of cesium-133. NIST has measured the frequency of its master cesium clock, NIST-F1, to within five parts in 1016. Frequency combs can transfer that standard to higher frequencies with great precision, but they also allow the use of optical clocks, which, in principle, promise finer resolution because of their higher frequencies.
“The core accuracy [of optical clocks] is just now moving past cesium clocks,” says Weiss. Microwave cesium clocks have the advantage of being extremely well characterized, but Weiss predicts that within the next 20 years the second will be defined in terms of some optical system. Several types are in development. So far, the highest reported accuracy is in a single-atom ultraviolet mercury clock developed by Jim Bergquist’s group at NIST.9 Jun Ye’s group at NIST has developed a clock that produces a much stronger signal by optically cooling and trapping an array of strontium atoms; it operates in the red at a lower frequency, 430 THz, with an uncertainty of less than 2 Hz.10
Outlook and implications
Frequency combs are an elegant technology in the best sense of the word, neatly combining different research threads into a powerful research tool that delivers important new capabilities. The field has already grown to an extent that it is hard to track all the activity.
We can expect frequency combs to continue probing the boundaries of physics, testing and refining theories and perhaps uncovering new phenomena that are impossible to see with less precise techniques. We’re beginning to explore the fundamental limits of frequency combs themselves. In the longer term, they may find practical applications that amaze us as new technologies require better and less costly clocks. Weiss points out that the precision clocks used in today’s Global Positioning System initially were developed as laboratory standards. The global telecommunications network will require ever-more-precise clocks as data rates increase, but when the future comes we’re likely to be surprised.
REFERENCES
1. J.L. Hall et al., IEEE J. Quant. Elect. 37, 1482 (December 2001).
2. H. Schnatz et al., Phys. Rev. Lett. 76, 18 (January 1996).
3. Theodor Hänsch, Nobel Lecture, http://nobelprize.org/nobel_prizes/physics/laureates/2005/hansch-lecture.html
4. J. Hall, Nobel Lecture, http://nobelprize.org/nobel_prizes/physics/laureates/2005/hall-lecture.html
5. J.D. Jost, J.L. Hall, and J. Ye, Optics Express 10, 515 (June 17, 2002 ).
6. M. Zimmermann et al, Optics Letters 29, 310 (2004).
7. S. Bize et al., Phys. Rev. Lett. 90, 150802 (2003).
8. E. Peik, et al., Phys. Rev. Lett. 93, 170801 (2004).
9. W.H. Oskay et al., Phys. Rev. Lett. 97, 020801 (July 14 ,2006).
10. M. Boyd et al., Science 314, 1430 (Dec. 1, 2006).
About the Author
Jeff Hecht
Contributing Editor
Jeff Hecht is a regular contributing editor to Laser Focus World and has been covering the laser industry for 35 years. A prolific book author, Jeff's published works include “Understanding Fiber Optics,” “Understanding Lasers,” “The Laser Guidebook,” and “Beam Weapons: The Next Arms Race.” He also has written books on the histories of lasers and fiber optics, including “City of Light: The Story of Fiber Optics,” and “Beam: The Race to Make the Laser.” Find out more at jeffhecht.com.