Attosecond laser pulses are measured by autocorrelation
Attosecond laser pulses are expected to become an important tool for probing ultrafast processes in chemistry and biochemistry. To optimize their generation, a reliable measurement of the pulse duration is essential. Until now, second-order autocorrelation—well known from femto- and picosecond laser physics—could not be used in the attosecond regime due to the short wavelength of attosecond pulses in the extreme-UV, their broad spectral width accompanied by a high dispersion when propagating in matter, their low intensity, and the lack of appropriate nonlinear detectors.
As a result, temporal measurements were restricted to cross correlation with the much longer primary laser pulse used for the attosecond-pulse generation. This limitation has now been overcome by researchers at the Max-Planck-Institut für Quantenoptik (Munich, Germany) and the Foundation for Research and Technology Hellas (Crete, Greece).1 The researchers have succeeded in making an autocorrelation measurement in the attosecond regime.
Superposed higher-order harmonics
To generate attosecond pulses, the researchers superposed phase-correlated higher-order odd harmonics of a primary 130-fs laser pulse at frequency ω, thus realizing a Fourier synthesis of a train of pulses, each with subfemtosecond duration and with center frequency at a multiple of ω. This procedure compares to femtosecond-pulse generation in lasers. Whereas in that case millions of modes in close spectral vicinity are modelocked in a laser resonator to form trains of femtosecond pulses, here only a few free-propagation waves of large spectral separation 2ω are superposed to form an attosecond pulse train, the phase correlation being provided by the method of harmonic generation. This was achieved by irradiating the 130-fs, 790-nm laser pulses across a xenon (Xe) gas jet; by photoionization of the Xe atoms and electron recombination, only odd harmonics are generated. When focused about 6 mm in front of the Xe jet, an optimal fixed-phase correlation of the harmonics was expected to result in a train of attosecond pulses for each 130-fs laser pulse.
In this way, odd harmonics up to the 15th at about 50 nm were generated. Using a filter made of a 0.2-µm-thick indium sheet, the fundamental, the third, and the fifth harmonics were blocked so that the center wavelength of a pulse was about 88 nm.
Harmonics 7 to 15 were selected to produce favorable conditions for the autocorrelation measurement—the central goal of the experiment. For the autocorrelation detector, the researchers used a jet of helium atoms combined with a time-of-flight mass spectrometer. Photon energies of the selected harmonics are not sufficiently high to ionize helium in a one-photon process; however, they may ionize helium in a two-photon process, which depends quadratically on pulse intensity. Thus, splitting the pulse train in half and superposing the halves in the helium jet with variable delay should cause the helium-ion yield to peak when optimal overlap is reached so that the full ion trace as a function of delay gives the autocorrelation trace from which the pulse shape can be deconvoluted.
By separately investigating the response of the helium-ion yield on pulse intensity for the different harmonics, the authors ascertained that two-photon processes were responsible for the ionization. In principle, a contribution of even higher harmonics could further shorten the pulses. However, such contributions would introduce some single-photon ionization, which would deteriorate the autocorrelation signal.
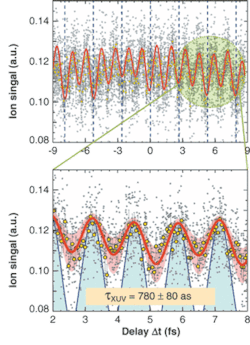
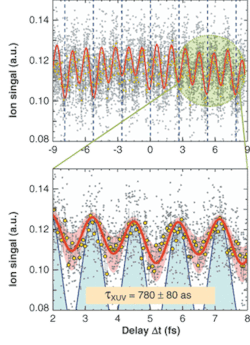
Special effort had to be made with respect to the beamsplitting and the variable delay, because any propagation in matter would cause dispersion, hence a broadening of the pulses. For this reason, a metallic concave mirror was cut into two halves, one of them being piezoelectrically translated to provide the variable delay. The focus of the mirror was positioned in the helium jet. The two-photon induced-ion detector signal peaks when the time- and focal-volume-averaged intensity reaches maxima, and passes a minimum in between when the corresponding intensity value becomes lowest, thus forming the autocorrelation trace (see figure). It allows deducing the duration of the attosecond pulses. The result is 780 ± 80 as—a value that is about twice as much as expected from a calculated superposition of the harmonics assuming perfect coherence. The considerable discrepancy between these two values raises questions about the assumption of perfect coherence.
Nonlinear (second-order) volume autocorrelation traces are measured in 37-attosecond (as) steps. In the18-fs-long trace of the superposition of the five odd harmonics 7th to 15th (top), 10 points are accumulated at each position (gray dots) and averaged (yellow points). Modulation with half the laser period is observable in the entire trace. The red curve is the best fit of an analytical function (a sum of a sequence of Gaussian pulses) with temporal width as the fit parameter, a best value being 1.1 fs—corresponding to an average duration (τ XUV) of 780 as for each extreme-UV pulse in the train (blue lines). The light-red shaded area indicates the scatter in the experimental points, giving an estimate for τ XUV of 780 ± 80 as.
It should be mentioned that the two-photon ionization of helium described here takes place in a volume, in contrast to the usual autocorrelation measurement in which two beams pass through a thin nonlinear crystal. Consequently, the contrast achieved here is not as high, although it is high enough to evaluate the pulse duration. The method does not suffer from any spectral dispersion, thus allowing application to even-shorter pulses. By using energy-resolved photoelectron detection, the method can be refined to provide a full temporal pulse characterization similar to FROGs (frequency-resolved optical gratings). In either configuration, the method is also well suited to measure subfemtosecond pulses from other sources, such as the emerging high-repetition-rate x-ray lasers.
Reference
- P. Tzallas et al., Nature 426, 20. November 2003, P. 267-270.