Spatial solitons of moderate power interact
Solitons are among the most fascinating objects in nonlinear optics. Not only are they a key issue for optical telecommunications, but they also promise to provide—in the form of spatial solitons—tools to steer light by light, which is of interest for all-optical logical devices and optical switching. For practical applications, however, fast switching at no greater than moderate intensities is a prerequisite.
Spatial solitons are optical beams of finite cross section that propagate in matter and form by self-trapping, a consequence of a strong interaction between the medium and the electromagnetic wave.1 In linear optics, optical beams undergo diffraction and diverge. Within nonlinear materials, on the other hand, self-focusing is a well-known phenomenon in which intense light locally increases the index of refraction (optical Kerr effect). Photorefractive as well as off-resonant quadratic and cubic nonlinear materials all allow the formation of spatial solitons. Photorefractive materials show only slow response to intensity variations, however, and off-resonant nonlinear materials require very high power. Furthermore, for forming stable self-trapped optical beams without detrimental optical breakdown, self-collimating must be limited by some saturation process.
Researchers at the University of Central Florida's Center for Research and Education in Optics and Lasers (CREOL; Orlando, FL) and Friedrich Schiller Universität Jena (Jena, Germany) have now achieved stable beam propagation of dissipative solitons in a longitudinally patterned semiconductor optical amplifier at moderate intensities and showed the dependence of their coherent interactions on relative phase.2, 3 Dissipative solitons require an additional balance of linear and nonlinear losses and gain. They form so-called zero-parameter families because their properties are completely determined by the system's parameters and not the optical input. Numerical simulations and measurements were performed. New phenomena could be observed such as "soliton birth."4
Self-trapped optical beams in semiconductor amplifiers were already demonstrated earlier; however, they did not propagate far enough for interaction studies because they were unstable. To achieve the new results, the researchers introduced a semiconductor optical amplifier made as a slab waveguide that was periodically patterned by gain and loss regions where the loss regions mimic a saturable absorber (SA) needed to stabilize the soliton (see Fig. 1). A 1-cm-long single indium gallium arsenide quantum well with its electroluminescence peak at approximately 950 m was sandwiched between two symmetric waveguiding layers and mounted on a copper carrier thermoelectrically cooled to 21°C. The amplifier was pumped via periodic gold electrodes arranged perpendicular to the propagation direction. Each electrode was 11 µm wide and 300 µm long and separated by 9-µm-wide silicon nitride insulator strips defining the SA regions.
Saturable absorption is key
The system showed either gain or loss, depending on the input intensity. The key idea for stable soliton generation is to use saturable absorption to damp out amplified spontaneous emission. Both the absorption in the nonpumped region and the amplification in the pumped region saturate at different intensity levels, however, so that negative net linear gain two stable steady-state plane-wave solutions (prerequisites for solitons) occur, the trivial one at zero power and another one at the higher intensity. This supplies stability for solitons. The dissipative soliton exists for a fixed intensity where the net gain for the full soliton beam amounts to zero. Any change in intensity changes the gain, driving the system back to this state.
To excite solitons and study their interactions, the relative phase of two beams from a continuous-wave Ti:sapphire laser emitting at 948 nm were controlled by splitting the beam with a Mach-Zehnder interferometer. The beams, each with a 38-mW power, were coupled into the waveguide with 15-µm-diameter waists on the entrance facet. The output of the 1-cm slab was imaged onto a CCD camera.
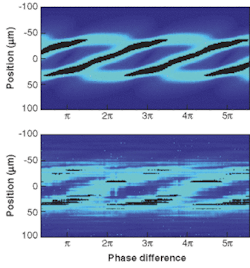
The researchers theoretically and experimentally investigated the interactions of two solitons generated by two parallel beams separated at the entrance by about one beam waist as a function of relative input phase. Depending on relative phase, the solitons fused and were steered in angle, except when the phase difference was p, at which point they were repelled so that two peaks of equal intensity were observed on the output facet about 22 µm apart, as expected for the coherent interaction.
Three solitons were theoretically predicted to appear at the output upon increasing the separation of the two in-phase parallel beams at the entrance facet to approximately 70 µm. The generation of the central soliton was explained by the nonlocal nature of the nonlinearity by which the carrier density profile formed a new central waveguide for the third soliton. At the start of propagation, the new soliton even showed higher intensity than the satellite ones, which diverged slightly.
Both the beamsteering as a function of relative phase and the appearance of a third soliton at multiples of 2p were clearly seen theoretically and experimentally (see Fig. 2).
The soliton interaction only disappears when the input-beam separation exceeds 100 µm. Similar soliton interaction was also observed for noncollinear, crossing trajectories that could be used for logic operations.
REFERENCES
- G. J. Stegeman and M. Segev, Science 286 (19 Nov. 1999).
- E. A. Ultanir et al., Opt. Lett. 28(4) (2003).
- E. A. Ultanir et al., Phys. Rev. Lett. 90(25) (2003).
- E. A. Ultanir et al., Opt. Lett. 29(3) (2004).