PHOTONIC FRONTIERS: SINGLE-CYCLE PULSES: Spectral broadening advances quest for single-cycle pulses
A single-cycle pulse seems the ultimate in ultrafast light. Pulse duration often is measured in units of time, and on that scale ultrafast physics has reached the attosecond (10-18 s) domain, with the current record at 80 as. Yet so far attosecond pulses have always contained several cycles of a high-frequency electromagnetic wave. Single-cycle pulses promise to be more powerful measurement tools and could help generate faster and cleaner attosecond pulses. Laser physicists have been seeking them for more than a decade.
Recent developments have finally reached the single-cycle realm with spectral broadening of near-infrared (NIR) lasers. Experiments with Ti:sapphire lasers at the Max Planck Institute for Quantum Optics (Garching, Germany) have achieved 1.5 cycle pulses. Alfred Leitenstorfer’s group at the University of Konstanz (Konstanz, Germany) used erbium-doped fiber lasers to reach a record 1.3 cycles. These results demonstrate impressive control over pulse generation.
The transform limit
The fundamental limit on generating ultrafast pulses is the transform limit arising from the uncertainty principle—the product of the pulse duration (time uncertainty ∆t) and spectral width (frequency uncertainty ∆ν) must equal at least 0.441.
∆t × ∆ν ≥ 0.441
These numbers show that it takes a very broad bandwidth to make a short pulse. Producing a 1 fs pulse nominally requires a spectral width of at least 441 THz—about the bandwidth of the whole visible spectrum. A 3 fs pulse requires a spectral width of about 150 THz, a third of the bandwidth needed for a 1 fs pulse.
The number of cycles in a pulse depends on the center frequency of the laser and the pulse duration. The longer the wavelength, the fewer cycles fit into a given pulse length. The lasers with the broadest bandwidth needed to produce the shortest pulses, including Ti:sapphire and erbium-doped fiber, emit in the NIR and a single-cycle pulse in that band would last a few femtoseconds.
Regardless of the pulse duration, generating single-cycle pulses requires spectral width greater than an octave. The natural gain bandwidths of Ti:sapphire and Er-fiber lasers are not an octave wide, but nonlinear techniques can stretch their emission across a broader supercontinuum of wavelengths. Considerable progress has been made over the past several years to generate supercontinua broad enough to produce few-cycle pulses approaching the single-cycle realm.
Ti:sapphire lasers
An early success came in 2003, when Keisaku Yamane of Hokkaido University (Sapporo, Japan) and colleagues split pulses lasting less than 30 fs from a Ti:sapphire amplifier centered at 790 nm into two beams, and passed one through a hollow optical fiber filled with argon. That broadened the spectrum to more than an octave, 495–1090 nm, which they then passed through a phase compensator to remove chirp, producing 3.4 fs pulses lasting 1.56 cycles—close to the transform limit they calculated at 3.0 fs.1
More recently, Stefan Rausch and colleagues at the Institute of Quantum Optics at Leibniz University Hannover (Hannover, Germany) developed an octave-spanning Ti:sapphire oscillator with emission from beyond 600 to 1200 nm. They phase-stabilized the system’s carrier-envelope offset using special dispersive mirrors and a pulse-shaping system to generate 4.4 fs pulses of about two cycles, but pulse energy was only about 1.25 nJ—although the 80 MHz repetition rate raised average power to 90 mW.2
Pulses lasting less than two cycles also have been produced by broadband parametric amplifiers, with output spanning 1200–2100 nm generating 8.5 fs pulses centered at 1.6 µm, the shortest pulses at that long wavelength.3
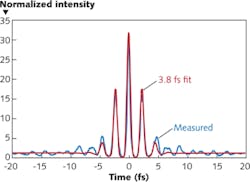
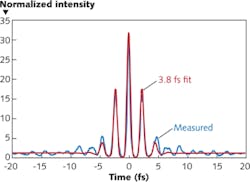
A team at the Max Planck Institute for Quantum Optics generated even shorter pulses—with full width at half maximum (FWHM) of about 1.5 cycles—from Ti:sapphire at much higher pulse energies. The NIR bandwidth of Ti:sapphire is sufficient to generate few-cycle laser pulses with proper dispersion management, but only at nanojoule pulse energies. Amplification to the millijoule level needed for high-harmonic generation causes gain-narrowing that reduces the spectral bandwidth. Self-phase modulation in a hollow-core fiber filled with a noble gas can produce a supercontinuum, which can be compressed to restore bandwidth, but powers had been limited to the microjoule level. The Max Planck group added a chirped-mirror pulse compressor to its amplifier, producing 1 mJ pulses that it compressed in a hollow-core fiber filled with neon to a duration of less than 4 fs—1.5 cycles at the nominal carrier wavelength of 720 nm (see Fig. 1).4
The production of self-referenced single-cycle pulses with phase stabilization of the carrier envelope is an enabling tool for producing attosecond pulses in the soft x-ray region, says Eleftherios Goulielmakis at the Max Planck Laboratory for Attosecond Physics (Garching, Germany; part of the Institute of Quantum Optics). Other groups have been generating attosecond pulses by producing high harmonics of multicycle femtosecond pulses in the infrared, he says, but that yields a series of attosecond pulses, one at the peak of each cycle in the IR pulse. With a single-cycle pulse, all the energy of the IR pulse can go into producing a single attosecond pulse, which is important because high-harmonic generation is inherently limited in efficiency.
In 2008, Goulielmakis and colleagues used that tool to generate high-harmonic pulses with a record duration of only 80 as.5 They reported that the electric field of their 3.3 fs, 1.5 cycle pulse at 720 nm ionized neon atoms in a gas jet, yielding a single high-harmonic pulse only just after the single peak of the IR pulse. Electrons pulled from gas atoms by the peak electric field recombine with the ionized gas and emit in the extreme ultraviolet (XUV) or x-ray region photons as the field declines. Generation of high-harmonic attosecond pulses starting from a multicycle pulse produces a series of attosecond pulses (see Fig. 2). Conversion efficiency was only on the order of 10-6, but the energy of the IR pulse was enough to generate about 0.5 nJ in the attosecond pulse.
Competition from erbium-fiber lasers
Erbium-doped fibers can’t match the gain bandwidth of Ti:sapphire and by themselves are limited to generating pulses in the 100 fs range. However, Er-doped fiber lasers emit in the 1550 nm band where silica fibers have anomalous dispersion, and thus can generate a broadband supercontinuum. Leitenstorfer’s group took advantage of these nonlinear effects to broaden erbium’s bandwidth beyond an octave.
In its first round of experiments, the Konstanz group started with an Er-fiber master oscillator modelocked at 49 MHz, which it coupled into a low-noise Er-fiber amplifier to generate pulse energies to 8 nJ. Silicon prisms compressed the pulses to 70 fs then coupled them through a precompression fiber into a highly nonlinear fiber, which produced a supercontinuum spanning 560 nm (FWHM). Recompression in another pair of prisms squeezed the pulses down to 7.8 fs, corresponding to two-cycle pulses centered on 1.17 µm. At the time, those were the shortest pulses generated with fiber laser technology.6
To create the broader spectral width needed for single-cycle pulses, Leitenstorfer took a different approach, dividing the output from a single fiber oscillator between a pair of amplifiers and nonlinear fibers to generate two separate supercontinua in different bands. Earlier efforts to combine two separate sources to form a single supercontinuum had failed, but the inherent stability of fiber laser technology allowed successful superposition to produce an ultrabroadband supercontinuum and single-cycle pulses.7
Output of a fiber oscillator modelocked at 40 MHz was split between two fiber amplifiers, which boosted average power of the modelocked pulse trains to 330 mW. Separate pairs of silicon prisms then compressed the output of each amplifier and coupled them into two different highly nonlinear fibers. One generated a broadband dispersive wave centered at 1125 nm; the other produced a broadband soliton centered at 1770 nm. Filtering left two supercontinua, one at wavelengths shorter than 1450 nm, the other at wavelengths longer than 1600 nm. Viewed separately, the shorter-wavelength pulses were two cycles long, and the longer wavelengths were several cycles. However, Leitenstorfer says that combining them through a variable delay line caused constructive interference in the middle and destructive interference at the edges, producing a single supercontinuum spanning 900 to 2100 nm. This produced 4.3 fs pulses spread over 1.3 cycles—the closest yet to single-cycle pulses (see Fig. 3).
Evolving trends
The pioneers in single-cycle pulses are extending their work. Leitenstorfer’s group has succeeded in passively phaselocking its single-cycle technology to an Er-fiber amplifier.8 That’s a significant step toward the phase control that is important in single-cycle pulses, says Leitenstorfer. “For an extremely nonlinear process in a single-cycle pulse, it matters if it’s a cosine or sine pulse,” because the cosine has a single sharp peak centered on the origin, compared to the negative and positive extremes on either side of the origin in a sine pulse. He’s also looking at taking advantage of the very broad bandwidth of thulium-doped fibers—from 1.8 to 2.2 µm—as another potential single-cycle technology. A key advantage of the fiber laser approach is its lower cost (in the $100,000 range), making it suitable for precision measurement, he adds.
In addition to exploring the attosecond frontier, Goulielmakis is investigating the synthesis of pulses even shorter than a single cycle. He seeks “the capability of controlling not at a single cycle, but at the sub-optical-cycle limit. Synthesizing sub-cycle waves would require spanning several octaves in wavelength or frequency,” from the IR into the visible, he says. The goal is to replicate in the optical band the powerful techniques used for waveform synthesis at microwave frequencies, and see if they could be used to control atomic motion on a femtosecond to attosecond scale.
REFERENCES
1. K. Yamane et al., “Optical pulse compression to 3.4 fs in the monocycle region by feedback phase compensation,” Opt. Lett., 28. 2258 (Nov. 15, 2003).
2. S. Rausch, “Controlled waveforms on the single-cycle scale from a femtosecond oscillator,” Opt. Exp., 16, 9729 (June 23, 2008).
3. D. Brida et al., Opt. Lett., 33, 741 (2008).
4. A.L. Cavalieri et al., “Intense 1.5-cycle near infrared laser waveforms and their use for the generation of ultra-broadband soft-x-ray harmonic continua,” New J. Phys., 9, 242 (2007).
5. E. Goulielmakis et al., “Single-cycle nonlinear optics,” Science, 320, 1614 (June 20, 2008).
6. A. Sell et al., “8-fs pulses from a compact Er:fiber system: quantitative modeling and experimental implementation,” Opt. Exp., 17, 1070 (Jan. 19, 2009).
7. G. Krauss et al., “Synthesis of a single cycle of light with compact erbium-doped fibre technology,” Nat. Photon., 4, 33 (2010); doi:10.1038/NPHOTON.2009.258.
8. G. Krauss et al., “All-passive phase locking of a compact Er:fiber laser system,” Opt. Lett., 36, 540 (Feb. 15, 2011).
About the Author
Jeff Hecht
Contributing Editor
Jeff Hecht is a regular contributing editor to Laser Focus World and has been covering the laser industry for 35 years. A prolific book author, Jeff's published works include “Understanding Fiber Optics,” “Understanding Lasers,” “The Laser Guidebook,” and “Beam Weapons: The Next Arms Race.” He also has written books on the histories of lasers and fiber optics, including “City of Light: The Story of Fiber Optics,” and “Beam: The Race to Make the Laser.” Find out more at jeffhecht.com.