PLASMONICS: Plasmonic nanostructures concentrate light
STEFAN A. MAIER
The field of metal-nanoparticle optics has come a long way from the spectral tuning of dipolar resonances via simple changes in particle shape. The exploitation of so-called dark modes via Fano resonances enables us to create nanostructures exhibiting a sharp spectral response and minimum scattering, while the novel tool of transformation optics provides a paradigm for the design of new classes of nanoscale optical cavities suitable for broadband light harvesting.
Resonance and its effects
Noble-metal nanoparticles with sizes smaller than the wavelength of visible light show strong resonances for light scattering and absorption, due to the excitation of localized surface plasmons. At resonance, light resonantly drives collective oscillation of the conduction electrons of the metal nanoparticle, which therefore acts as a radiating dipole. Its resonance frequency is strongly dependent on particle shape and dielectric environment, which enables tuning of its "color" throughout the visible and into the near-infrared (IR) regime of the spectrum, while keeping particle size well below 100 nm.
The most prominent application of this effect has been all around us during history, in the form of colored glass, incorporating metal nanoparticle dopants. More modern applications, increasingly at a single-nanoparticle level, lie in the tagging of biomolecules, enhancement of light emission from nanoscale photon sources, and biomolecular sensing.1,2 All of these exploit the fact that at their dipolar resonance frequencies, metal nanoparticles enable nano-concentration of light below the diffraction limit around the particle surface, and feature resonantly enhanced absorption and scattering cross-sections.
Controlled nanofabrication, and particularly electron-beam lithography, now enables us to create metallic nanostructures consisting of multiple metallic elements with controlled relative placements down to distances on the order of 10 nm (see Fig. 1a). This provides a simple yet compelling way to not only tune the resonance frequencies of the system, but also the interaction strength with radiation, via exploitation of near-field coupling between neighboring units.
Bright and dark modes
Take the simplest case of two dipoles interacting. Depending on whether their dipole moments are aligned parallel or anti-parallel with each other, the respective coupled modes will either show a stronger or weaker interaction with far-field radiation—the normal modes of a dimer system hence consist of a spectrally broad bright (superradiant) mode, and of a spectrally narrow dark (subradiant) mode. With the concept of bright and dark modes, the balance between absorption and scattering of plasmonic nanocavities can be controlled.
In essence, metal nanoparticles can be understood as classical harmonic-oscillator systems at the nanoscale, and many features of collective resonances in simple geometrical arrangements can be conceptually modeled as masses on springs. Interactions between localized plasmons in more complex geometries can be elegantly understood within the concept of plasmon hybridization.3
Beautiful physics arises in appropriately designed systems where a spectrally narrow resonance of a dark mode overlaps with a spectrally broad bright mode: in analogy to quantum systems of a localized state interacting with a continuum, Fano resonances appear. At these resonances, linear destructive interference between two excitation pathways of the bright mode (directly, or via coupling with the dark state) lead to quenching of scattering, and hence an increase in transmission in a spectrally sharp window (see Fig. 1b and c). These effects were experimentally demonstrated in a number of plasmonic nanosystems at the single-particle level, such as dolmen-type structures or disk/ring cavities.4,5 Most spectacularly, a stacked arrangement of three metallic bars has been shown to quench scattering completely due to a Fano effect, leading to a nanostructure which only absorbs light, but does not scatter.6 Fano resonances have now been shown in an increasing number of plasmonic nanostructures, and also in metamaterials, promising exploitations in highly sensitive biological sensors, dispersive elements for slow-light metamaterials waveguides, and nanoscale light sources.7
Transformation optics
Another concept that is quickly developing into a whole new paradigm for the design of nanoscale plasmonic cavities is that of transformation optics, which is based on the fact that Maxwell's equations stay invariant under coordinate transformations. Developed initially within the field of metamaterials for the design of fascinating elements such as optical cloaks, and recently applied with the goal of routing propagating surface-plasmon polaritons, transformation optics has now been shown as a powerful tool for the design and analytical understanding of nanoscale plasmonic cavities.8-11 The concept is simple: Start with a simple plasmonic system whose interaction with radiation can be solved analytically, and then apply a suitable transformation of space in order to transform it into a more geometrically complex nanocavity—or vice versa. Due to the invariance of Maxwell's equations under the transformation, this allows us to derive analytical expressions for the absorption and scattering cross-sections. But not only that—it also provides a way to solve a persistent problem in photonics: how to design a small cavity that efficiently harvests light over a broad spectral range. Such a device could find a large number of applications, from solar-energy collection to applications in multispectral sensors and nonlinear switching units.
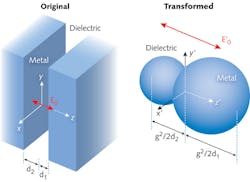
A broadband or continuous spectrum is usually associated with an infinite plasmonic system. A simple example is a single metallic plane or a thin dielectric layer sandwiched between two metallic spaces. Such a system can draw energy from a nearby point dipole at all frequencies up to the surface-plasma frequency of the system; the energy radiated by the dipole is collected in the form of surface-plasmon polaritons that propagate to infinity, losing their energy via absorption by the metal in the process. However, by applying a suitable geometrical transformation, we can now "fold" such an infinite planar system into a highly compact nanocavity. The simplest example is an inversion, leading to cavities with a structural singularity. Applied to the aforementioned planar example of the metal/dielectric/metal sandwich, this leads, in three dimensions, to a system of touching nanospheres (see Fig. 2), and in two dimensions to touching nanowires. As a second example, an inversion applied to the single metal/dielectric interface transforms the system into a two-dimensional, crescent-shaped wire.Broadband energy concentration
Under the inversion, energy formerly transported out to infinity in the planar system is now efficiently carried to the structural singularity—in the case of touching units to the "kissing point," and in the case of the crescent to its tip (see Fig. 3). And because the infinite system shows a broadband optical response, so does the transformed nanoscale system—these cavities have been demonstrated to harvest light efficiently over a broad spectral range, tunable via the aspect ratio of the crescent or the touching wires/spheres.11 Within the limits of classical electromagnetism and the neglect of nonlocal effects in the immediate vicinity of the singularity, field enhancements up to three orders of magnitude can be anticipated, confirmed by full-field electromagnetic simulations. Such hot spots for broadband energy concentration could be exploited for example for surface-enhanced Raman scattering, or nonlinear nanodevices and light sources, if suitable active media are placed into them.Clearly, an inversion is only one of a whole host of possible mathematical transformations, turning this concept into a very general paradigm for the design of novel plasmonic nanocavities.12 The fact that now analytical theory can be applied to nanocavity design will not only enhance the tool kit of nanoplasmonics, but also allow a deep physical insight into the light harvesting and spectral properties of plasmonic nanosystems. Intriguingly, even radiative cavity losses can be analytically modeled using this concept.13 Clearly, fabrication of suitably smooth cavities with singularities remains a significant challenge, but spectral scalability extends transformation optics also to lower frequencies, for example for energy collection and routing in the terahertz window where fabrication-accuracy requirements are less stringent, using suitable plasmonic materials such as indium antimonide instead of metals.
The underlying concepts presented here—Fano resonances and geometrical transformations—have been exploited in various areas of optics already for decades. That they now experience a renaissance in nanoplasmonics is a further testament to the power of this emerging field marrying modern photonics with nanotechnology.
ACKNOWLEDGMENTS
The author thanks Yannick Sonnefraud, Alexandre Aubry, Dang Yuan Lei, and Antonio Fernández-Domínguez for designing the artwork.
REFERENCES
1. S. Maier, Plasmonics—Fundamentals and Applications, Springer (NY, 2007).
2. Brongersma and Shalaev, Science, 328, 5977, 440 (2010).
3. Prodan et al., Science, 302, 5644, 419 (2003).
4. Verellen et al., Nano Lett., 9, 4, 1663 (2009).
5. Sonnefraud et al., Acs. Nano., 4, 3, 1664 (2010).
6. Liu et al., Nat. Mat., 8, 9, 758 (2009).
7. Luk'yanchuk et al., Nat. Mat., 9, 9, 707 (2010).
8. Pendry et al., Science, 312, 5781, 1780 (2006).
9. Huidobro et al., Nano Lett., 10, 6, 1985 (2010)
10. Liu et al., Nano Lett., 10, 6, 1991 (2010).
11. Aubry et al., Nano Lett., 10, 7, 2574 (2010).
12. Aubry et al., Phys. Rev. Lett., 105, 233901 (2010).
13. Aubry et al., Phys. Rev. B, 82, 205109 (2010).
Stefan A. Maier is codirector of the Centre for Plasmonics & Metamaterials at Imperial College London; e-mail: [email protected]; www3.imperial.ac.uk/plasmonmeta.