CRYPTOGRAPHY: SLED-based true random-number generator is scalable in output
A true random-number generator (RNG) developed by a group of Chinese and American researchers can generate two simultaneous, independent 10 Gbit streams of random bits from a setup based on a superluminescent LED (SLED).1 The approach has the potential to produce 20 or more simultaneous streams of random bits.
True RNGs are of vital importance to cryptography, and are also used for scientific applications, as well as by lottery services, and even artists and musicians. Pseudo-RNGs are simpler than true RNGs but less useful, because the numbers they generate show signs of nonrandomness.
There is a great difference between the two types of tools. A pseudo-RNG takes the form of a computer algorithm that produces a sequence of random-seeming numbers by taking an initial set of values and doing some number-crunching on them. One characteristic of a pseudo-RNG algorithm is that if you give it the same set of initial values, it will always produce the same final sequence.
In contrast, a true RNG relies on some physical phenomenon to inject real randomness into its result. A web search will reveal many sites that present pseudo-RNG algorithms but far fewer that describe a true RNG. One of these sites is www.random.org, which says that its RNG relies on atmospheric noise to produce randomness. Other approaches to true RNG behavior include photon counting, chaotic lasers, and even detection of quantum fluctuations in the vacuum.
Even a “true” RNG can have nonrandom bias. Because of this, the National Institute of Standards and Technology (NIST; Boulder, CO) developed a series of stringent tests for randomness that an RNG needs to pass before it can be called a true RNG. The SLED-based RNG passes these tests.
Simple and compact system
The researchers, who are from Beijing Normal University (Beijing, China) and the University of Maryland (College Park, MD), start with a commercially available broadband fiber-coupled SLED, coupling two wavelength-division-multiplexing filters to it to produce two channels at 1540 and 1555 nm, each with a 2.2 nm optical transmission bandwidth. The channels are each detected by an 11 GHz photoreceiver. The two narrow spectral slices each result in an electrical signal whose rapid fluctuations are much greater than the background electrical noise.
A clocked comparator for each signal is set to threshold-detect the signal, producing a sequence of random bits (checked against an external 10 GHz clock signal) that are then processed by bit-error-rate testers (BERTs). Data acquisition is initiated by an external trigger so that both channels are started at the same time and synchronized.
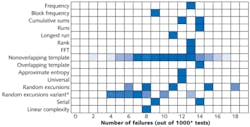
While the two resulting bitstreams showed no interchannel correlation, statistical testing did show a deviation from true randomness. But the researchers demonstrated that doing an exclusive-OR (XOR) operation between each bitstream and a time-delayed copy of the bitstream (with delays as short as 26 bits) produced, to all appearances and tests, true randomness. In addition, the result of the XOR showed no apparent correlation with the original sequences. (The XOR was computed offline but could easily be done in real time, say the researchers.)
The NIST statistical tests (all 188 of them) were applied to the data. To pass, there must be no more than 19 failures per 1,000 trials (except for one test, the random-excursion variant test, which requires no more than 13 failures out of 561 trials). The XOR-processed data passed all tests for both optical channels (see figure). The researchers also took the bit sequence from both channels, sequentially interleaved them, and subjected the result to the NIST tests, which again gave a passing grade.
Because the SLED has a broadband 75 nm spectrum, many more channels could easily be added to the setup. For example a 20-channel device using a single SLED would generate random bits at a rate of 200 Gbit/s. The system uses only compact commercial components, and could be integrated at the board or even chip level for ultrahigh-rate true random-number generation.
REFERENCE
1. X. Li et al., Opt. Lett., 36, 6, 1020 (Mar. 15, 2011).
About the Author
John Wallace
Senior Technical Editor (1998-2022)
John Wallace was with Laser Focus World for nearly 25 years, retiring in late June 2022. He obtained a bachelor's degree in mechanical engineering and physics at Rutgers University and a master's in optical engineering at the University of Rochester. Before becoming an editor, John worked as an engineer at RCA, Exxon, Eastman Kodak, and GCA Corporation.