Nonlinear Phenomena: Photonic-crystal fiber shifts ultrashort-pulse wavelengths

Jan. 1, 2006

When a femtosecond laser pulse is sent through a length of optical fiber, the output pulse is often very different from the input pulse.

Uwe Brinkmann

FIGURE 1. An ultrafast pulse entering a photonic-crystal fiber has a broadband spectrum (left). The group-velocity dispersion (right ordinate) is shown for two different photonic-crystal fibers 1 (core diameter 1.6 µm) and 2 (core diameter 1.8 µm); a cross-section photo of fiber 1 is seen in the inset. The pulse temporal envelope and phase chirp are seen at bottom.

When a femtosecond laser pulse is sent through a length of optical fiber, the output pulse is often very different from the input pulse. Intrinsically spectrally broad, an ultrafast pulse undergoes normal dispersion when traveling along the fiber; in addition, with the laser field strongly confined to the fiber core, resulting high peak pulse intensities cause nonlinear optical effects. For example, the high intensities modify the index of refraction, causing self-phase modulation to accumulate. Stretching in time and further spectral broadening are the normally expected results. Using photonic-crystal fibers (PCFs), however, researchers recently found results that are much more interesting, both in their physics and in their possible applications.

A team of researchers from Max-Planck-Institut für Quantenoptik (Garching, Germany), Ludwig-Maximilians-Universität München (Munich, Germany), and Lomonosov State University (Moscow, Russia), showed both theoretically and experimentally that a sub-6-fs Ti:sapphire laser pulse, fed into a specially designed PCF, splits into different pulses, one of them even growing into a soliton that continuously shifts to longer wavelengths during travel. Thus, from the Ti:sapphire laser pulse dominated by a 670‑nm peak, pulses at peak wavelengths up to 1064 nm and even longer could be produced.^1,2

Varying dispersion

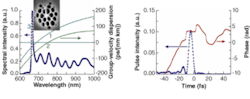
The researchers used two PCFs with core diameters of 1.6 and 1.8 µm, respectively (see Fig. 1). Photonic-crystal fibers allow “tailoring” of the dispersion properties. The dispersion curves of the two fibers are shifted in relation to one another, providing zero group-velocity dispersion (GVD) at markedly different wavelengths. Positive GVD values correspond to anomalous dispersion, in which longer-wavelength radiation propagates more slowly. The position of zero GVD with respect to the spectrum of the input pulse is important for the spectral and temporal transformation of the pulse propagating along the fiber.

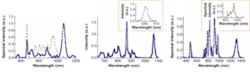
The experimental results matched theory when nonlinear effects were taken into account. For a comparison, the authors used a nonlinear Schrödinger equation that included a term describing Raman scattering related to phonons. Phonons, together with other nonlinear interactions, were the essential contribution accounting for the experimental results.

FIGURE 2. For 0.3-nJ input pulses, the input spectrum (above, dashed line) for a 20-cm length of fiber 2 is compared with the output (above, solid line). The output spectrum has developed a red-shifted maximum. Continuous tuning to the red can be realized by increasing the fiber length. A 23-cm length of fiber 1 produces a soliton spectrum for the output peak centered at 1060 nm (center, inset). In addition, the shape of the input spectrum—changeable by the dispersion characteristics of the laser mirrors—influences the position of the isolated peak (right ). The other peaks emerge from further nonlinear interactions or are higher-order fiber modes, and can be readily filtered out.

In some cases, spectral peaks corresponding to soliton pulses emerge (see Fig. 2). With the time duration of the soliton pulse on the order of 100 fs and with precise time and spectral control achievable by dispersion-engineering in optical fibers, experiments to produce amplified few-cycle pulses can be made, for example by seeding a Nd:YAG laser. The group recently used a red-shifted soliton, formed by sub-6-fs laser pulses in a PCF, to significantly simplify pulse synchronization in the parametric amplification of few-cycle field waveforms.³

REFERENCES

1. E.E. Serebryannikov et al., Appl. Phys. B 81, 585 (2005).

2. E.E. Serebryannikov et al., Phys. Rev E 72, 056603 (2005).

3. C.Y. Teisset et al., Optics Express 13, 6550 (2005).