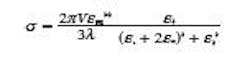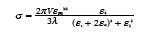PLASMONICS: Gold nanoparticles are shaped for effect
The resonances of noble-metal nanoparticles depend on their geometry-nanoshells, nanorods, or even nanocages can be created to achieve specific results. Further, their resonances can be tuned to match a particular application.
JASON HAFNER
Noble-metal nanoparticles have become the basis for a new class of optical nanosensors, and have other applications as well. In just one example, gold nanoparticles with plasmon-resonant absorption in the near-IR (NIR) can be used to photothermally destroy cancerous tumors in mice. The nanoparticles are injected intravenously and collect at the tumor; because tissue is relatively transparent in the NIR, the nanoshells can be illuminated from outside the body to locally heat and destroy the tumor. The useful properties of noble-metal nanoparticles are intimately tied to their geometry.
Such nanoparticles exhibit strong optical scattering and absorption at visible and near-IR wavelengths due to localized surface-plasmon resonance (LSPR). This is a classical effect in which the light’s electromagnetic field drives the collective oscillations of the nanoparticle’s free electrons into resonance. The effect was theoretically described by Mie in 1906 by solving Maxwell’s equations for a metal sphere surrounded by a dielectric medium using the dielectric function of the bulk metal.1
Although LSPR has been understood for more than 100 years, the field has recently experienced significant growth because of advances in three areas: the reproducible synthesis of nonspherical nanoparticles with tunable plasmon resonances; numerical techniques to calculate optical properties of nonspherical nanoparticles; and applications of plasmon-resonant nanoparticles in nanophotonics, chemical sensing, and biomedical engineering.
Many gold and silver nanoparticle structures have recently been developed, including nanoshells, nanorods, and nanocages. A key feature of these nanoparticles is that their resonances are tunable, which enables one to set the LSPR at a laser wavelength or spectral region that matches a particular application.
Gold nanoshells
In the dipole approximation, which is applicable to nanoparticles that are much smaller than the wavelength of light, Mie theory is reduced to a simple expression that accurately predicts the LSPR wavelength for small gold nanospheres:
Where σ is the extinction cross section (scattering + absorption), V is the nanoparticle volume, λ is wavelength, εm is the dielectric constant of the medium, and ε1 is the real part and ε2 is the imaginary part of the dielectric function of the metal. The resonance condition is met when ε1 = -2εm, around λ = 520 nm for gold in air. The sharpness of the resonance is determined by the imaginary part of the dielectric function, ε2.
Silver, having a smaller imaginary component than gold, exhibits sharper, brighter resonances. However, the surface chemistry of gold is in general less reactive and easier to work with. As gold nanospheres grow in size and approach the radiation wavelength, the full Mie-theory solution accurately predicts a limited red shift of the LSPR wavelength and a significant broadening of the resonant lineshape, thus limiting several of their potential applications. However, broad tunability can be achieved with a core/shell structure.
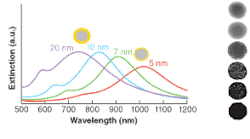
In 1998, Naomi Halas at Rice University demonstrated that one could create such nanostructures by growing a thin layer of gold onto a spherical silica nanoparticle.2 The silica nanospheres are first terminated with thiols so that 2- to 3-nm gold nanoparticles can be attached to the surface. The gold shell is then fully formed by the reduction of gold ions to grow and fuse the small gold nanoparticles on the surface. This synthetic method allows independent control over the core and shell radii. The gold nanoshells exhibit an LSPR resonance that varies with the ratio of inner and outer shell radii and can be tuned from the visible to mid-IR (see Fig. 1). Through control of the two radii, nanoshell extinction can be designed to be primarily due to scattering or absorption, enabling applications for cancer detection and therapy.
Nanoshells also exhibit predictable near-field enhancements for rational surface-enhanced Raman-spectroscopy (SERS) experiments. The SERS technique can detect ultralow concentrations of complex molecules, including hazardous agents, with molecular specificity. Most experiments are carried out on rough metal films with poorly defined optical properties; with gold nanoshells, however, a plasmon resonance can be tuned to the excitation laser wavelength for a predictable, reproducible surface enhancement.
Because the nanoshells are spherically symmetric, their resonances can be analytically described by Mie theory. However, one can gain an intuitive understanding of their resonances by considering plasmon hybridization. Both a gold nanosphere and a spherical cavity in bulk gold will exhibit LSPR. When these structures are brought together to form a nanoshell, the plasmon resonances interact and form hybrid plasmon resonances at different energies. This plasmon hybridization theory is essentially an electromagnetic analog of molecular orbital theory and can be applied to gold and silver nanostructures with arbitrary shapes.3
Gold nanorods
Gold nanorods are solid gold cylinders approximately 10 to 20 nm in diameter and 40 to 200 nm in length. They are synthesized by nanoparticle growth in the presence of a surfactant, which is thought to bind the nanoparticle surface and generate growth anisotropy.4 Although the growth mechanism is not understood in detail, gold nanorods can be synthesized simply and in high yield by seed-mediated methods developed by Catherine Murphy of the University of South Carolina (Columbia, SC) and Mostafa El-Sayed of the Georgia Institute of Technology (Atlanta, GA).
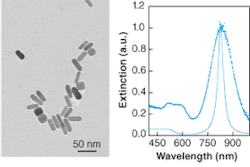
The extinction spectrum of gold nanorods exhibits a longitudinal plasmon resonance resulting from excitation along the nanorod length. The wavelength of this resonance is tunable through the visible and NIR by varying the nanorod aspect ratio. Because of the nonspherical shape, nanorod extinction cannot be described by Mie theory. However, qualitative features of nanorod resonances are well reproduced by Gans theory, an extension of Mie theory for spheroidal nanoparticles.5 Gans theory puts depolarization factors for each direction in the Mie-theory expression to capture the optical anisotropy. A comparison can be made between the nanorod extinction spectrum and a Gans-theory simulation (see Fig. 2).
Given that Gans theory is only a qualitative approximation for nanorods, more-exact numerical calculations based on the exact nanorod geometry, such as the dynamic dipole approximation (DDA) and T-matrix methods, can be applied. Gold nanorods are unique because of their sharp resonances and their relatively small size, with their diameters approaching the molecular scale. Because the LSPR of small, dipole-limited particles is dominated by absorption, nanorods are best suited for applications that benefit from localized heating. Applications have recently been demonstrated in photothermal therapy and imaging of cancer, mercury sensing, and drug delivery.
Gold nanocages
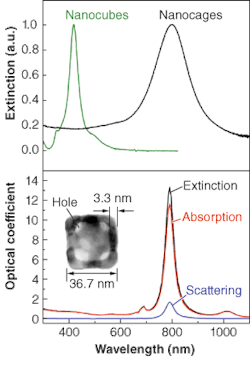
Younan Xia of the University of Washington (Seattle, WA) recently described the synthesis of gold nanocages.6 Like nanoshells, these nanoparticles have tunable plasmon resonances because of the presence of a dielectric core. In nanocages, however, the core is empty rather than composed of silica. Gold nanocages are grown over a silver nanocube template. The monodisperse nanocubes are made by a polyol process, such as reduction of silver nitrate in ethylene glycol in the presence of poly(vinylpyrrolidone). These template particles are then exposed to a solution of gold ions, which replace the more-reactive silver on the nanoparticle surface. Gold grows around the silver nanocube surface and the silver is dissolved into solution, leaving gold nanocages (see Fig. 3).
The typical edge length is 37 nm and the typical thickness 3 nm. The overall size can be tuned by adjusting the size of the initial nanocube template. The cage thickness and porosity can be varied by varying the ratio of nanocube and gold ion concentration. The extinction spectrum of fully formed nanocages exhibits a peak at 800 nm, ideal for biomedical applications such as targeted optical-coherence tomography. The extinction peak can be tuned from 400 to 1200 nm by adjusting the geometrical parameters. The optical extinction of structurally complex nanoparticles like the gold nanocages cannot be simulated by Mie theory. This structure was analyzed by numerical techniques, and the resulting spectra matched the experiment. Although one might not expect a hollow structure with thin gold walls to be mechanically stable, the gold nanocages do not deform upon drying for analysis by electron microscopy. Still, the nanocages are not likely to be as stable as nanoshells with a solid dielectric core.
While it is well known that nanostructures represent materials with essentially tunable properties, a more recent trend is to create highly complex nanostructures in terms of shape and composition to achieve enhanced functionality. The nanoparticles described here represent just a few paths toward tunability. Other possibilities include silver nanoprisms, for which DDA calculations from Chad Mirkin and George Schatz of Northwestern University (Evanston, IL) indicate that the LSPR wavelength is sensitive to the corner sharpness.7 Also, the synthesis of branched nanoparticles and the controlled formation of nanoparticle dimers and larger aggregates result in multispectral optical properties. With continued development in their synthesis and assembly, noble metal nanoparticles will be a standard stock of future nanophotonics applications.❏
REFERENCES
1. G. Mie, Annalen Der Physik25, 377(1908).
2. S. J. Oldenburg et al., Chemical Phys. Lett. 288, 243 (1998).
3. E. Prodan, et al., Science 302, 419 (2003)
4. J. X. Gao et al., Langmuir19, 9065 (2003).
5. S. Link et al., J. Phys. Chem. B103, 3073 (1999).
6. J. Chen, et al., Nano letters5, 473 (2005).
7. R. C. Jin et al., Science294, 1901 (2001).
JASON HAFNER is an assistant professor of physics and astronomy at Rice University; 6100 Main St., Houston, TX 77005; e-mail: [email protected].