PHOTONIC FRONTIERS: SLOW LIGHT: Slow light looks good for optical buffers
Slow light first gained wide attention as one of those intriguing physics experiments that made headlines by doing something that the public thought was impossible-slowing light waves down to a veritable crawl. The trick was to go to a logical extreme-slowing down light by tuning light to a wavelength where a material had an extremely high refractive index. That meant tuning the wavelength to match a resonant wavelength in an atomic vapor.
Those early experiments did not point directly to practical applications because the atomic vapors were cooled below the threshold for Bose-Einstein condensation. But they suggested that more-practical techniques might be useful for optical-data buffers that could store signals in optical form for telecommunications and signal processing. During the past several years, researchers have made steady progress toward that goal. For example, a recent theoretical study concluded that there was no fundamental limitation on pulse delay.1 In addition, a Defense Advanced Projects Agency (DARPA; Washington, D.C.) project on slow light has stimulated various important developments reported in March at the Conference on Optical Fiber Communications (OFC; Anaheim, CA) and in July at the Optical Society of America’s Topical Meeting on Slow and Fast Light (Washington, D.C.).
Making atomic resonances transparent
Normally, the sharp increase in refractive index at a resonance is accompanied by a similar increase in absorption, so the more a material slows light down, the higher its absorption. Steve Harris at Stanford University (Palo Alto, CA) circumvented this problem by illuminating the atomic vapor with another laser beam tuned to a resonant transition in a three-level system, electromagnetically inducing transparency on that transition, which otherwise would have strongly absorbed the slow light. In 1995 his group used this approach to slow light by a factor of 165 in lead vapor.2
Slow light hit the headlines in 1999, when Lene Hau at Harvard University (Cambridge, MA) slowed light by a factor of 17 million to 17 m/s.3 The spectacular result came from cooling sodium atoms below the 435 nK threshold for Bose-Einstein condensation. This allowed a low-power laser beam to produce electromagnetically induced transparency in a narrow band of wavelengths where refractive index varies steeply, producing very high dispersion.
The spectacular results surprised physicists, but it was not immediately clear how to make practical use of a system operating at ultracold temperatures. Another major limitation was the extreme narrowness of the resonances, which limited the slowing effect to a narrow range of light frequencies-meaning that the delays were largest for long pulses, which contain only a limited range of frequencies.
The technique can be extended to atomic-vapor resonances above room temperature, which are well suited for proof-of-principle experiments because they “are clean, beautiful systems describable by Schrödinger’s equations,” says Robert Boyd of the University of Rochester. John Howell of Rochester pumps hot rubidium vapor with a laser tuned between a pair of hyperfine absorption resonances separated by 3 GHz. Variation of resonant input power and frequency modulation of the pump laser allows Howell to tune delays by up to 50 times the length of the input pulse (see Fig 1).4
Coherent population oscillations in solids
An effect called coherent population oscillation occurs in solid saturable absorbers that can produce the high spectral dispersion and low absorption needed to slow the velocity of light in a room-temperature solid. A powerful pump beam interacts with a signal beam slightly offset in frequency to cause coherent variation of the ground-state population at the difference frequency, affecting the group refractive index at the signal frequency. The effect was first observed in ruby and has also been seen in other saturable absorbers, including erbium-doped glass and semiconductors.
As with atomic vapors, the bandwidth available for slow light is limited, in this case by the population recovery time in the solid. Early experiments were limited to bandwidths in the kilohertz range, but last year saw bandwidths to 2.8 GHz in a semiconductor optical amplifier.5 This year, Boyd’s group reported 17 GHz bandwidth in lead-sulfide quantum dots, achieving a 10% delay of 25 ps pulses.6 That takes it into the speed range needed to delay data bits arriving at 10 Gbit/s, a speed widely used in backbone telecommunications. However, the delay remains short when compared to the pulse length, and the technique is limited to wavelengths at which saturable absorption occurs.Stimulated scattering in solids
The coherent interactions involved in stimulated Brillouin and Raman scattering in optical fibers offer an alternative way to slow the speed of light in solids.
In stimulated Brillouin scattering, an intense pump beam transfers energy to a weak signal beam that is offset from the pump by a characteristic acoustic frequency. This causes refractive index to vary strongly at wavelengths where stimulated Brillouin gain occurs. An important advantage is that light is slowed at a wavelength offset from the pump beam by a material-dependent frequency, so that picking the right pump band can place the delayed wavelength into the standard telecommunications bands.
The natural bandwidth of the Brillouin resonance is only about 100 MHz, which limits data rate to tens of megabits per second. However, the bandwidth can be extended by spreading the pump light across a wider band of frequencies and using highly nonlinear fiber. This weakens the resonance, but raising the pump power can compensate for the loss. At OFC, Dan Gauthier and his team at Duke University (Durham, NC) reported reaching Brillouin bandwidth of 12.6 GHz in 2 km of highly nonlinear fiber, allowing them to delay a 75 ps pulse by 47 ps. The group said that higher gain should allow them to delay pulses by a full pulse length.7 That speed also allows 10 Gbit/s operation.
Alex Gaeta’s group at Cornell University (Ithaca, NY) has slowed light using stimulated Raman scattering in conventional optical fibers. The broader bandwidth of Raman scattering can accommodate shorter pulses than Brillouin scattering or other methods. Yet the change in refractive index is also spread across this frequency range, so the spectral dispersion is lower and becomes nonlinear at the edges of the band. Gauthier says this makes it essential to match the signal speed to the resonance width to achieve optimum delay. Last year, Gaeta’s group used this approach to delay 430 fs pulses by up to 85% of the pulse duration, showing the potential to handle data rates well over 40 Gbit/s.8
Raman scattering is particularly strong in silicon, opening prospects for slow light on chips. Gaeta and Michal Lipson at Cornell demonstrated tunable delays to 4 ps for 3 ps pulses in an 8 mm nanoscale waveguide, with bandwidths of 100 GHz.9
More recently, Lipson demonstrated a tunable optical delay in a different type of optical chip, with a pair of ring resonators coupled to a pair of waveguides tangent to each of them. The two rings resonate at slightly different frequencies, producing a coherent coupling that works like electromagnetically induced transparency to produce a delay to about 17 ps by thermal turning (see Fig. 2).10Applications of slow light
The main attraction of slow light is as a variable delay for signal processing and data buffering. Packet switching is a highly efficient way to allocate telecommunications transmission capacity, but it requires a variable-delay buffer that can hold data bits while a packet switch reads and acts upon the address stored in the header bits. Currently, that means optical packets must be converted to electronic format for processing and buffering, then converted back into optical form for transmission from a packet switch.
Optical buffering is a demanding task. For telecommunications backbone applications, it should be able to handle inputs at 10 Gbit/s or more and blocks of at least 1000 bits, the equivalent of a delay of 1000 pulse lengths. That’s beyond the capabilities of current technology. “I don’t think anyone has stored a whole sequence of bits,” says Gauthier, noting that his team has gotten about one pulse width of delay in Brillouin-scattering delay experiments.
Improvements are possible, but even a single-bit delay can be useful in regenerating a pulse train that has become distorted in a fiber. A delay of 0.5 to 1 pulse length is enough for resynchronization to get pulses back into their proper time slots, Gauthier says. That capability also might be useful in quantum information processing. Howell wants to see if his rubidium system can preserve the wave function while delaying light.
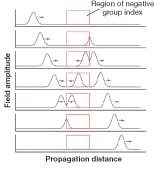
And that’s only the start. “There’s much more in the pipeline,” says Boyd. His group has demonstrated superluminal velocities in alexandrite and the backward propagation of pulses in erbium-doped fiber amplifiers (see Fig. 3).11, 12
REFERENCES
1. R.W. Boyd, et al., Phys. Rev. A 71, 023801 (2005).
2. A. Kasapi et al., Phys. Rev. Lett. 74, 2447 (1995).
3. L. Hau et al., Nature 397, 594 (1999).
4. R. Camacho et al., Physical Rev. A 73, 063812 (June 13, 2006).
5. X. Zhao et al, Optics Express 13, 7899 (2005).
6. G. Piredda et al., paper MC6 at Slow Light Conf.
7. Z. Zhu et al., OFC 2006 Postdeadline Papers.
8. J. Sharping et al., Optics Express 13, 6092 (Aug. 8, 2005).
9. Y. Okawachi et al., Optics Express 14, 2317 (March 20, 2006).
10. Q. Xu et al., Optics Express 14, 6463 (July 10, 2006).
11. M.S. Bigelow et al., Science 301, 200 (July 11, 2003).
12. G.M. Gehring et al., Science 312, 985 (2006).
About the Author
Jeff Hecht
Contributing Editor
Jeff Hecht is a regular contributing editor to Laser Focus World and has been covering the laser industry for 35 years. A prolific book author, Jeff's published works include “Understanding Fiber Optics,” “Understanding Lasers,” “The Laser Guidebook,” and “Beam Weapons: The Next Arms Race.” He also has written books on the histories of lasers and fiber optics, including “City of Light: The Story of Fiber Optics,” and “Beam: The Race to Make the Laser.” Find out more at jeffhecht.com.
![FIGURE 2. Thermal tuning of the double-ring silicon waveguide resonator (top) produced time delays that could be tuned thermally in experiments by Michal Lipson’s group at Cornell University. The consequent relative delays are plotted at bottom [10]. FIGURE 2. Thermal tuning of the double-ring silicon waveguide resonator (top) produced time delays that could be tuned thermally in experiments by Michal Lipson’s group at Cornell University. The consequent relative delays are plotted at bottom [10].](https://img.laserfocusworld.com/files/base/ebm/lfw/image/2016/01/th_0610lfw_04f2.png?auto=format,compress&fit=max&q=45?w=250&width=250)