Photonic Frontiers: Coherent Atoms: Coherent atoms are on the move
Coherent atoms have become “hot” despite the ultracold temperatures needed to form the Bose-Einstein condensate that makes them coherent. The wave-particle duality tells us that atoms can be described as matter waves, and coherence highlights the wave nature of atoms. Now, 11 years after the first Bose-Einstein condensate, researchers are exploring the behavior of coherent atoms, which often resembles that of coherent light.
Experiments have demonstrated effects in coherent atoms that are the equivalent of familiar optical effects. Nonlinear atomic optics produce the atomic equivalent of four-wave mixing. Atomic states can be squeezed in a way similar to optical states. Atom amplifiers, oscillators, mixers and splitters have been proposed or demonstrated. The principles of atom optics are being extended further, to devise atom interferometers, storage rings for cold atoms, and quantum atom optics. A new generation of “atom chips” is making the technology more accessible than it was in the days when cooling atoms to within a tiny fraction of a degree above absolute zero was a true “hero experiment.”
Bose-Einstein condensates
The crucial breakthrough was Bose-Einstein condensation, produced by cooling atoms to temperatures so cold that they dropped into the lowest possible quantum state. Identical atoms with integral spin-called bosons-can simultaneously occupy this lowest possible quantum state and have the same phase. Condensation occurs below a threshold temperature that depends on atomic mass and particle density, and corresponds to the point where the de Broglie wavelength of the atoms is close to the average spacing between them. Below that threshold, the atoms become coherent in phase and energy, like the stimulated emission that forms a laser beam.
Similar equations describe matter waves and light waves, but atoms are not photons, and their behaviors differ. Condensates are superfluids, able to move without friction like electrons in a superconductor. Atoms have mass and internal states that have no counterparts in photons. Atoms also interact with each other directly, without requiring the nonlinear material that mediates the interactions of photons with each other. This means that atomic processes can be quite different from their photonic analogs such as “lasers,” nonlinear optics, and amplification.
One example is the emission of coherent atoms by a Bose-Einstein condensate in an “atom laser,” first reported by Wolfgang Ketterle’s group at MIT in 1997.1 At first glance, an atom laser sounds similar to an optical laser. Both generate coherent waves within a cavity that are coupled to the outside world. In the atom laser, the cavity is a magnetic trap, and the atoms remained trapped inside it until coupling is changed. In the MIT experiments, a radio-frequency pulse excited some trapped atoms into an unconfined state so they could fall out of the trap. Later experiments used other methods, but none of the experiments actually generated new atoms, unlike optical lasers which generate new photons.
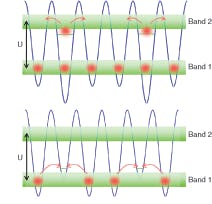
Four-wave mixing also has an atomic counterpart, in which three de Broglie waves mix to produce a fourth wave (see Fig. 1). In the atomic case, the nonlinearity comes from interactions among the atoms rather than from the transmission medium. Similar equations describe the two processes, but atomic four-wave mixing does not create a new atom. Instead, two of the atomic de Broglie waves interfere with each other to create an atomic standing wave, with alternating regions of high and low density, and this standing wave diffracts the third atom, converting it into the fourth wave without creating another atom. This is equivalent to Bragg scattering of atoms, and requires careful choice of the momenta of the three input atoms to conserve energy and momentum, the atomic equivalent of optical phase matching.2
A variant on the four-wave process can amplify matter waves. In this case, two inputs are atom waves and one is an optical laser beam. The initial experiment at the University of Tokyo created a weak de Broglie wave within the condensate, which interfered with the rest of the condensate to create a matter-wave grating.3 This matter-wave grating scattered photons from a laser pulse, which transferred momentum to atoms remaining in the condensate, and those scattered atoms effectively amplified the weak de Broglie wave. Recently Ketterle’s group has reported that extensions of this technique could create entangled pairs of atoms.4
Atom chips
Early experiments with coherent atoms were complex and difficult, but recent advances are making the experiments much easier. An important advance is the development of “atom chips,” in which permanent magnets, electromagnets, and other components are placed on a substrate to control motion of atoms above the surface.“The chip can include particle reservoirs, waveguides, beamsplitters, detectors, [and can] even include control devices,” says Dan Stamper-Kurn of the University of California at Berkeley. Laboratory versions are starting to get impressive results, and Stamper-Kern says they could lead to practical applications such as inertial and rotation sensors.
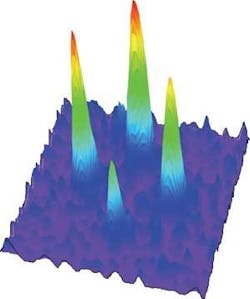
In an important experiment last year, Joerg Schmiedmayer’s group at the University of Heidelberg (Heidelberg, Germany) demonstrated the first atom chip able to perform matter-wave interferometry.5 The key component was an atom-chip version of a beamsplitter, which split a Bose-Einstein condensate in two. The splitter consists of a pair of wires, one carrying about 1 A of direct current, the other carrying a 60 mA current oscillating at 500 kHz. Together they form a magnetic trap for atoms. Slowly changing the radio-frequency field splits the magnetic trap so it has a pair of minimum potentials (see Fig. 2). This splits the condensate into two pieces that can later be recombined to measure the dynamic phase evolution of the two fully separated samples.
Last year Stamper-Kurn’s group demonstrated another key capability-storing a Bose-Einstein condensate in a circular waveguide that functioned as a millimeter-scale storage ring.6 Such particle reservoirs could be included on atom chips, and used to create precision rotation sensors. Stamper-Kurn’s group also tamed instabilities called betatron oscillations. In high-energy storage rings, betatron oscillations can cause losses of charged particles, but they turn out to slow the dispersion of ultracold atoms in the miniature waveguide rings. Reducing dispersion effectively cools ultracold atoms, and experiments demonstrated betatron cooling from about 40 nK to below 100 pK, important for improving atom interferometry.7Prospects for “Atomtronics”
A team at JILA and the University of Colorado in Boulder has proposed a family of atomic analogs of electronic components, which they call “atomtronics.”8 They envision placing ultracold atoms in a spatially periodic field such as the standing wave formed by a pair of counterpropagating laser beams. That electromagnetic lattice creates periodic potential wells analogous to the forces that the crystalline lattice of a semiconductor applies to electrons moving within the solid. Adjusting potential levels can create defects that affect the trapping of atoms like the impurities in p- and n-doped semiconductors affect electron motion (see Fig. 3).
Such potential fields can confine atoms in ways similar to the way quantum wells, quantum wires, and quantum dots confine electrons. The researchers envision creating the atomic equivalent of diodes and transistors, which in turn could lead to atomic counterparts of simple electronic circuits such as logic gates and flip-flops. Condensates are superfluids, making them the atomic counterparts of superconducting diodes, but analogs of conventional diodes and transistors may also be possible.
“It’s obviously something that offers a lot of interesting potential,” says Murray Holland of the JILA-Boulder team. Dana Z. Anderson, another member of the group, is working on demonstrating devices.
Research on coherent atoms is still in the early stages, and other concepts are sure to emerge. Quantum atom optics hasn’t taken off yet, but is expected to do so. “That’s one I think is going to happen,” Stamper-Kurn says. He’s working on nondestructive measurements of atomic state for quantum computing, something not possible with photons. Mark Raizen at the University of Texas in Austin has demonstrated atomic-number squeezing, an essential step toward quantum computing with atoms.9 Developers also are intrigued by the potential for extremely precise measurements with the short de Broglie wavelengths of atoms. Much more is yet to come.
REFERENCES
1. M.R. Andrews, et al. Science 275, 637 (1997).
2. S.L. Rolston and W.D. Phillips, Nature 416, 219 (March 14, 2002).
3. M. Kozuma et al., Science 286, 2309 (Dec. 17 1999).
4. G. Campbell et al., “Parametric amplification of atoms,” arXiv:cond-mat/0509302 (May 19, 2006).
5. T. Schumm et al., Nature Physics 1, 57 (October 2005)
6. S. Gupta et al., “Bose-Einstein condensation in a circular waveguide,” www.arxiv.org/pdf/cond-mat/0504749 (April 28, 2005).
7. K.W. Murch et al., “Dispersion management using betatron resonances in an ultracold atom storage ring,” www.arxiv.org/pdf/cond-mat/0508765 (Aug. 31, 2005).
8. B. Seaman et al., “Atomtronics: ultracold tom analogs of electronic devices,” www.arxiv.org/pdf/cond-mat/06066252 (Jun 23, 2006).
9. C.-S. Chuu, et al., Phys. Rev. Lett. 95, 260403 (2005).
About the Author
Jeff Hecht
Contributing Editor
Jeff Hecht is a regular contributing editor to Laser Focus World and has been covering the laser industry for 35 years. A prolific book author, Jeff's published works include “Understanding Fiber Optics,” “Understanding Lasers,” “The Laser Guidebook,” and “Beam Weapons: The Next Arms Race.” He also has written books on the histories of lasers and fiber optics, including “City of Light: The Story of Fiber Optics,” and “Beam: The Race to Make the Laser.” Find out more at jeffhecht.com.
![FIGURE 2. An initial single Bose-Einstein condensate is split by changing the magnetic field applied to the trap. The condensate is suspended below an atom chip, confined by the magnetic field from current passing through a pair of conductors in experiments at the University of Heidelberg [5]. FIGURE 2. An initial single Bose-Einstein condensate is split by changing the magnetic field applied to the trap. The condensate is suspended below an atom chip, confined by the magnetic field from current passing through a pair of conductors in experiments at the University of Heidelberg [5].](https://img.laserfocusworld.com/files/base/ebm/lfw/image/2016/01/th_0609lf03f2.png?auto=format,compress&fit=max&q=45?w=250&width=250)