Ray tracing expands optical design
Ray tracing expands optical design
John Tesar
Skilled optical designers will want to use both sequential and nonsequential ray tracing programs, in addition to CAD software, to fully evaluate their systems. This article explains some of what ASAP--a nonsequential ray tracing program from Breault Research Organization (Tucson, AZ)--does; ASA¥is not, however, a program to do sequential ray tracing or lens design. Element shape, count, and material choices are best done in specialized lens-design programs with their powerful optimizers and algorithms.
The nature of the traced rays themselves delineates the principal difference between classical lens-design programs and ASAP. Snell`s law defines how a ray moves through system space interacting with the elements within by refractive index differences. Material interactions cause rays to change speed and bend.
Lens-design programs treat this process sequentially, that is, each element is considered in order before moving on to the next. Each ray is a delta function that incorporates the dispersive properties of the materials and perhaps a few additional parameters, depending on the program. The precise flux values--power and irradiance--of each incident ray are tracked in ASAP. Each ray is allowed to split at each refracting surface into transmitted (refracted) and reflected rays in proportion to the assigned transmittance and reflectance of the surface. Additionally, each interaction of a ray in a system can be characterized by absorption as well. The rays are traced in the order that they are transmitted and that reflected components require, regardless of the order of the component in the system. Rays that want to back u¥and out of the system can.
In ASA¥a ray is a beam with shape--a Gaussian beam centered around the base ray. There are upwards of 70 parameters associated with each ray as it propagates through the system. These can include a partial history of where it has been, its polarization state, its coherency, and more.
Geometric modeling is general in ASAP, allowing it to support the introduction of CAD files and their inherent ability to model almost any shape. In effect, a model built in a CAD program can be transported to ASAP; optical characteristics can be assigned to components, and rays can be traced in one unified optomechanical model with both geometric and wave optic qualities. This property makes ASA¥powerful for designing, analyzing, and simulating complex systems. ASA¥is CAD-compatible with either DFX or IGES formats and with its own 3-D visualization. ASA¥has always been a fully geometry-based ray-tracing environment.
The designer or system analyst can make the ray go in any desired direction; after the parameters are defined, the geometry can be built in any way wanted. Rays can be turned loose in a world where almost anything is permitted, and when the analysis is done, the important information is chosen. ASA¥is not restricted to a limited number of analysis functions. Out of the 70 history items stored on each ray there are an almost unlimited number of combinations for evaluation. A designer is not limited to modulation transfer functions (MTFs), spot diagrams, or ray fans, for example. These parameters can be used in the lens-design phase.
Because MTF is not a physical quantity, ASA¥does not calculate it directly. What is measured is the image distribution, and to get an MTF in ASAP, an image-processing algorithm is applied by computing the point spread function with a Fourier transform. The primary goal of ASA¥is to give the user data on physical quantities anywhere in the system, although secondary characteristics such as MTF (which is really post- processing of data) are supported. The distribution of energy--the real point spread function--is of interest.
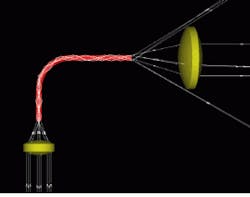
An evaluation plane can be moved anywhere within the system and the energy distribution calculated and evaluated in a myriad of ways. ASA¥makes no distinction nor does it discriminate preferentially for surfaces or conventions such as image plane, aperture stop, and exit or entrance pupils. These conventions are artifacts of thinking of optical systems as imaging systems. In ASAP, rays are fired at the system and if apertures cli¥rays they cli¥rays--those rays simply do not make it to the detector plane (see figure on p. 219).
The global coordinate system in ASA¥is an engineering, or mathematical, approach to geometric modeling rather than the traditional optical approach of treating objects as inter related entities. Dummy surfaces and folding paths are eliminated. When ASA¥was developed in the early 1980s, it incorporated notions of a global coordinate system. Other codes added these capabilities as its programmers incorporated nonsequential raytracing. Extremely difficult as well as routine problems are possible to solve with ASAP, which makes visualizing systems easier.
A surface is a mesh or a grid of points, and the issue is whether, between the points, the surface is straight or not. Basic nonsequential ray tracing programs use a linear model between grid intersections, but ASA¥is capable of rendering any surface through the use of two-dimensional arrays of three-dimensional points. Bidirectional import and export of data via IGES (Initial Graphic Exchange Specification) NURBS (non-uniform rational B-splines) is supported.
Design applications
Interferometers are a class of instruments requiring nonsequential ray tracing of coherent beams, splitting and recombining beams, to view the interference effects. When ASA¥is used to model these instruments, it keeps track of optical path length, the absolute phase of the ray, relative phase in conjunction with polarization states, and the effects of multilayer dielectric coatings. Interferometric techniques can also be simulated with its wave optics propagation algorithm. A coherent beam can be propagated through a laser cavity and alignment optics, for example. The beam will automatically split into reflected and transmitted components at any beamsplitter, and the beams can be recombined to produce interference fringes.
Grazing incidence ray paths are a class of problems suited to ASAP. Intersecting ray algorithms fail at grazing incidence. Whether they are grazing or near-normal, ASA¥traces rays through and from optical elements with complex geometries. These could be lenses, of course, but could also be a taurus, a sphere, a cone, a tube, or machined geometries from exotic optical materials. Other machined components with unusual scattering properties assembled between or enclosing the optical elements can be modeled.
Stray light analysis is also suited for ASAP. Rays traced through a laser system, for example, are split into transmitted and reflected components at each lens, window, or filter to simulate the generation of ghost rays. These can be traced through the system to find their locations in three-dimensional space. In high-power lasers, information on ghost focus locations can be used to avoid placement of delicate components at these places. Quantitative calculations of ghost irradiance across any plane in the system can be used to design beam dumps that will safely and effectively handle ghost radiation.
Treats imaging and nonimaging designs
Neither imaging nor nonimaging systems are favored by ASAP. Nonimaging systems present more-difficult problems. A ray fan plot is of no interest in automotive headlam¥design. Source modeling, particularly of extended sources, is of interest to transportation lighting designers, who are concerned with modeling the spatial emission pattern of an arc because it differs with wavelength. The radiant flux also differs with wavelength, and the geometry of the bulb affects the far-field intensity pattern. Once a realistic model is created or measured, it can be joined with lenses or elements to evaluate the potential performance.
A current class of design problems requiring the strengths of both nonsequential and sequential ray tracing programs is that of a liquid-crystal-display (LCD) projector. Extended source modeling can be joined with lens-design capabilities, for example, to find the best solutions. Both the imaging and nonimaging portions can be modeled in ASA¥and the total system evaluated. Assuming typical efficiency for LCD projectors is about 3%, there is plenty of room for more design, simulation, and analysis.
Deforming a component or perturbing the system allows "what if?" experiments to be run in ASAP. If a collection of variables is changed, the likely effect at the detector will be known. The ability to handle wave optics places ASA¥at the high end of optical-analysis tools for combined imaging and nonimaging systems.
As a comprehensive generalist, ASA¥is not just for on-axis or paraxial systems; bends, folds, beamsplitters, and intermediate image positions with a mix of imaging and nonimaging optics are routinely handled. Complicated systems such as those for laser fusion, which have deformable mirrors where ghosting is problematic, are not beyond the scope of its analysis tools. o
Ray tracing with ASA¥in this fiber-coupled endoscope design reveals rays that are clipped and fall outside the plane. Such analysis could assist in determining the effectiveness of an optical design.
JOHN TESAR is vice president of sales at Breault Research Organization, 6400 East Grant Rd., Tucson, A¥ 85715.