Macro photon simulations aid nonimaging optical design
Macro photon simulations aid nonimaging optical design
Sergei Ivanov and David Lovering
Ray-tracing methods have been used successfully for a long time as simulation tools for optical design. And, as computers have become cheaper and faster, ray-tracing methods have been applied to other types of simulations involving energy radiation. In some areas, such as nonimaging optics, however, intrinsic limitations sometimes prevent ray-tracing methods from providing satisfactory results.
Software using an alternative simulation method based on particles is currently under development at Animation Science Corp. (ASC; Sunnyvale, CA). This method has been designed to simulate radiative energy transfer through space by modeling the flow of particles, each of which represents a certain amount of energy.
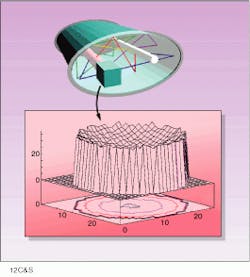
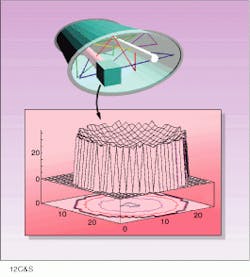
To date, a particle-tracing simulation system has been used to simulate global illumination from lighting fixtures and for simulation of a solid-state laser-pumping process with good results. In such situations, the particles can be thought of as "macro" photons. These macro photons propagate through space according to the laws of optics. Although this model is very natural from the physicist`s point of view, it has not been widely used before and offers a number of advantages in simulating, in particular, the behavior of modern laser systems (see figure).
Uniform pumping
Modern laser systems use a variety of techniques to pump energy into the active medium to achieve the required population inversion for laser operation. At any point within the active medium, the optical gain depends on the optical characteristics of the material and also on the degree of population inversion. In this scenario, homogen eity of the laser gain profile critically affects system performance in terms of stability, beam quality, and energy-extraction efficiency.
Traditional laser-pumping schemes are usually designed to optimize the uniformity of the pumping, often by using combinations of large (inefficient) flashlamps and diffuse reflectors. The low efficiency of most laser media also leads to heating, and the resulting thermal stresses and refractive-index variations give rise to thermal lensing.
In addition to accounting for refraction and reflection, as well as scattering and absorption of light as it propagates from the pump into the active medium, computer simulations of these complex processes must also account for the absorption spectrum of the active medium and the emission spectrum and spatial emission characteristics of the pump radiation. Also, if metallic or dielectric reflectors are used, al lowance must be made for possible energy-distribution variations in the laser medium due to wavelength dependence of reflection characteristics.
New laser designs
New technologies such as diode-laser pumping and monolithic resonators pumped via lightguides make optimizing the pump configuration of new laser designs increasingly difficult. None of the commonly encountered simulation technologies--such as ray-tracing or radiosity analysis--can address all of the requirements encountered in laser pump design. Briefly, these are
To calculate a three-dimensional map of the population inversion (and hence laser gain) inside the gain medium
To calculate a three-dimensional map of the liberation of heat within the gain medium
To take full account of any emission, reflection, or absorption spectra, both during the simulation and in the analysis of the results
To model the emission characteristics of the pump sources, such as the divergent, astigmatic beam emitted by a diode laser
To simulate the propagation and redistribution of the pump energy taking full account of the (possibly anisotropic) reflection characteristics of all surfaces.
Particle-simulation software offers a means for satisfying these requirements, however. The approach being developed by ASC is based on a proprietary particle-tracing engine capable of tracing the trajectories of millions of point-like particles simultaneously. Any number of sources and objects with which the particles interact can be used to define the initial conditions of the simulation. When the simulation begins, particles (macro photons for our nonimaging optics simulation) are emitted into the simulation scene according to the spatial and wavelength probability distributions assigned to the sources. One of the major differences between particle-tracing and traditional ray-tracing is that when macro photons are simulated their properties are calculated at each time step of the simulation and not only at the intersections with surfaces.
Beneath the surfaces
As a consequence, a unique property of this system is the ability to incorporate volumetric effects--optical phenomena that occur inside the objects rather than just at surfaces. Once imported from almost any CAD/CAM system, the optical properties of each object can be defined using an intuitive graphical user interface or by editing a script file. Refractive index, optical attenuation coefficient, absorption, and scattering probabilities inside objects can be defined as constants, functions, or tables of wavelength or position.
Particle-tracing systems also permit wide flexibility in defining the optical properties of object surfaces within the simulation. One can specify what fraction of photons is scattered, absorbed, or transmitted through the surface and whether scattering is specular or nonspecular. Similar to volumetric para meters, surface properties can be defined as constants, functions, or tables of wavelength or position. Statistical results also can be ob tained in either surface or volume mode, and the user can accumulate statistical data using properties of each particle (its wavelength, for example).
Modeling radiation as particles allows for a very natural introduction of Monte Carlo methods into various aspects of the simulation. For instance, if we assign a certain probability of nonspecular scattering at a surface, then each macro photon upon reaching the surface would be redirected by the simulation to continue its motion in accordance with the outcome of the Monte Carlo trial. In nonsequential ray-tracing, however, the nonspecular reflections are implemented in a more abstract fashion, by splitting an incident ray into several reflected rays (usually a fixed number).
Statistical precision
Another advantage of the particle-tracing simulation system is that the precision of statistical results is governed purely by the total number of particles emitted during the simulation. Therefore, for preliminary studies a small emission rate can be set, thereby increasing the simulation speed. (The simulation speed is inversely proportional to the number of particles in the simulation at any time. And for multiprocessor architectures it is almost directly proportional to the number of processors installed.)
Statistical analyses can be used to estimate the precision of the numerical results. But as a rule of thumb it, most of the numerical results tend to follow Poisson`s distribution for which (on average) the signal-to-noise ratio is equal to the square root of the mean value.
Particle-tracing technology offers a fresh approach for modeling radiation in computer simulations. When fully developed and implemented, the technology will probably be used to solve an array of problems in the fields of lighting, optical systems, lasers, and thermal transfer. o
Particle-based simulation can describe volumetric as well as surface effects and optical layout of modern laser systems, such as this elliptic laser pumping chamber containing a flashlam¥and Nd:YAG rod. The end of the rod on the left side of the chamber is enclosed inside a cubic "statistics box." The horizontal plane in the three-dimensional graph below the chamber represents a "statistics plane" or vertical cross section through the statistics box. The vertical axis in the graph represents photon absorption at each pixel in the statistics plane, and the entire structure is cut in half by a statistics plane. The simulation was generated using predefined object geometries.