Simulation tools solve light-scattering problems from biological cells
Biological cells can be considered as dielectric objects with a given refractive-index distribution. Consequently, light-scattering simulations provide an efficient tool for studying cell morphology as well as the nature of scattering and its sources. The finite-difference time-domain (FDTF) aproach enables researchers to simulate light-scattering from single cells in situations in which other approaches do not work or the approximations inherent in them are questionable.
The FDTD method is effective for this application because it enables the modeling of a large variety of light-propagation phenomena and material effects such as scattering, diffraction, reflection, refraction, absorption, and polarization effects.1 The method can also successfully model material anisotropy, dispersion, gain, and nonlinearities without any preassumptions and approximations for the nature of the optical field and its behavior. The method is extremely well suited for the design and analysis of submicron structures and devices with very fine structural details.
The FDTD approach is based on the direct numerical solution of time-dependent Maxwell's equations. It uses the so-called Yee's numerical scheme implementing central difference approximations for the numerical derivatives in space and time. The sampling in space is on a subwavelength scale. Typically, 10 to 20 steps per wavelength are needed. The sampling in time is selected to ensure numerical stability of the algorithm.
In optics, a submicron device scale implies a high degree of light confinement and, correspondingly, the necessity for a large refractive-index difference of the materials (mostly semiconductors) to be considered. In the simulation and modeling of light-scattering from microbiological structures such as single biocells or clusters of cells this necessity does not apply.
Microbiological objects can be considered as complex dielectric objects with a given refractive-index value distribution (usually varying in the range of 1.3 to 1.7) and light-scattering simulations provide us with an efficient tool for studying the morphology of the objects as well as the nature of scattering and its sources. The analysis of this information is the basis for a better understanding and development of new optical methods for noninvasive biomedical diagnostics.
Why FDTD?
The development of noninvasive optical methods requires a fundamental understanding of how light scatters from structures within tissue. For example, light-scattering spectroscopy and optical coherence tomography are directly related to the measurement of light-scattering parameters. It is very important to understand from what microbiological structures light scatters, and the sensitivity of light-scattering parameters to the dynamic changes of these structures. Also, if possible, it is valuable to relate these changes quantitatively to measured light-scattering parameters. Light scattering from single biological cells and nuclei is currently under intensive investigation in the scientific and research literature.2, 3, 4
Researchers generally agree that the dimensions of scattering centers are less than 1 µm and, therefore, much of the scattering must be from small structures within the cells' nuclei and cytoplasmic organelles. Mitochondria have been recognized as a major source of scattering. Phase-contrast microscopy studies show that nuclei and nucleoli cause significant phase shifts compared to other cell components and are also expected to be a major source of light scattering.
Simulations using FDTD of light scattering from cells have significantly contributed to understanding the role of cell morphology on light-scattering patterns. The FDTD approach has demonstrated its unique ability to estimate the accuracy of the currently used analytical and numerical techniques as well as of their approximations. In addition, it provides valuable information about the interaction of light with a single cell. It was found, for example, that the overall shape of the nucleus influences small-angle scattering whereas the effects of small intracellular organelles, or high-frequency index-of-refraction fluctuations, are more evident at higher angles.
Simulation results
The FDTD simulation results discussed here are based on two-dimensional (2-D) and 3-D dielectric models of the cell. The simulations were performed by the OptiFDTD software (Optiwave; Ottawa, ON) and by a separate 3-D FDTD program with a built-in far-field calculation procedure.5 During the simulation process, scattering patterns—that is, the plot of the intensity of scattered light as a function of angle—are extracted. From a scattering pattern it is easy to estimate the relative magnitude of scattered light power at different angles and compare the results from multiple simulations accounting for particular features of cell's shape, composition, or morphology.
We restricted our consideration to simple cell morphologies and focused on accounting for the effect of two different factors on light-scattering patterns. First, the effect of absorption in the medium surrounding the cell. Previous studies have shown that accounting for absorption in the host medium influences the light scattering distributions from phytoplankton cells, which are of prokaryotic type and do not have a well-formed nucleus.5
Second, the effect of the deviation from the ideal spherical shape of the cell and, in particular, the effect of the elongation of the cell in one of the space dimensions. Previous studies based on the T-matrix method have shown that alignment of red blood cell volume-equivalent spheroids, sphering, and elongation have a significant influence on the angular distribution of the scattered light.6
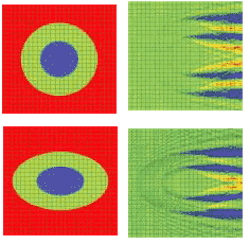
A 2-D simulation shows a single cell situated in a computational domain with periodic boundary conditions on the two opposite sides along the direction of propagation (see Fig. 1, top and bottom). The refractive indices values are cytoplasm 1.37, nucleus 1.4, and extra-cellular medium 1.35. The near-field electric-field distribution in this case is equivalent to the case in which an infinite vertical row of cells is considered.
FIGURE 1. A simulation shows the refractive index (top, left) and electric near-field amplitude (top, right) distribution around one of the cells in a vertically oriented infinite row of periodically positioned circular cells with a period of 24 µm; the radii of the cell and of the nucleus are 8 and 4 µm, respectively. Blue and red colors (right) correspond to min and max values of the electric-field amplitude. The refractive index (bottom, left) and electric near-field amplitude (bottom, right) distribution around one of the cells in an infinite row of periodically positioned elliptical cells with a period of 24 µm has cell radii of10 and 6.4 µm, respectively. The longer and shorter nucleus radii are 5 and 3.2 µm, respectively.
Comparing the results of the simulation demonstrates the effect of small cell-shape variation on the electric near-field distribution around the cell. Slight changes to the electric-field distribution in the near field will lead to significant field changes in the far-field zone and will be detectable in an experiment.
In the 3-D simulations, a 2-µm-radius spherical cell contains only a cytoplasm (n = 1.37) and a nucleus (n = 1.4, radius 1 µm). The extra-cellular medium has a refractive index value n = 1.35. The dimensions of the cell are intentionally minimized, which significantly relaxes the intensity of the computational efforts. Our interest was in demonstrating the ability of the FDTD method to model various important features of cell morphology and in particular absorption in the extra-cellular medium. To study the effect of the absorption of the extra-cellular medium in 3-D, we assume that the refractive-index value of the extra-cellular medium has a real and an imaginary part: n+iκ. Three cases for the complex value of the extra-cellular refractive index were considered: 1.35+i0.00, 1.35+i0.01, and 1.35+i0.05.
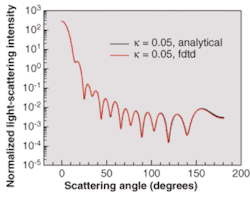
Validating the results of the simulation of this effect requires implementing advanced numerical boundary conditions such as the so-called unsplit perfectly matched layer (UPML) boundary conditions.5 The wavelength of incident light used in the simulations is 900 nm. The space resolution in all directions is equal to λ/30. The time step ensures numerical stability of the algorithm. We have validated our 3-D FDTD simulation results by comparing them to the results based on a recently developed analytical technique (see Fig. 2).7
The normalized light-scattering intensity can be viewed as a function of the scattering angle for three values of the imaginary part of the refractive index of the surrounding host medium (see Fig. 3). It is clear that increasing the imaginary refractive index of a cell's surrounding medium significantly modifies the angular distribution of light-scattered intensity. Higher absorption in the extra-cellular medium increases the scattering intensity for larger values of the scattering angle.
This fact must be taken into account when studying the scattering efficiency of biological-tissue light-scatterers in general. It shows that the analysis of light scattering from isolated biological cells does not necessarily account for the whole effect of the surrounding medium. Considering an effective absorption in the extra-cellular material is more realistic in terms of averaging the global effect of the external light-scatterers in the proximity of the cell.
In sum, relatively small changes of cell shape or the parameters of the extra-cellular medium can significantly change the angular distribution of the scattered light. The successful application of the FDTD technique requires an adequate knowledge about cellular dielectric structure and parameters; it is also a powerful tool for building a deeper understanding about them and a better understanding of existing and new optical methods for noninvasive biomedical diagnostics.
REFERENCES
- A. Taflove and S. Hagness, Editors, Computational Electrodynamics, Arthech House Publishers, Boston, 2000.
- R. Drezek et al., Applied Optics 38(16) 3651 (1999).
- J. R. Mourant et al., J. Biomedical Optics 5(2) 131 (2000).
- R. Drezek et al., J. Biomedical Optics 8(1) 7 (2003).
- W. Sun et al., Applied Optics 41(27) 5728 (2002).
- A. M. K. Nilsson et al., Applied Optics 37(13) 2735 (1998).
- W. Sun et al., J. Quantitative Spectroscopy Radiation Transfer (in press).
STOYAN TANEV is program manager of photonics and biophotonics programs at Vitesse Re-Skilling Canada, 1200 Montreal Rd., M-50, Ottawa, ON, Canada K1A 0R6; WENBO SUN is research assistant professor at the Center for Atmospheric Sciences of Hampton Uniersity, Hampton, VA; RICHARD ZHANG is a research scientist at Optiwave, 7 Capella Court, Ottawa, ON, K2E 7X1; ANDREW RIDSDALE is group leader of the confocal microscopy, image data analysis, and visualization group at Ottawa Health Research Institute, 725 Parkdale Ave., Ottawa, ON, Canada K1Y 4K9; e-mail: [email protected]