Ray-trace software characterizes radiation transfer in systems

Walk across a parking lot at noon, stand next to a window on a summer day, or sit next to a warm computer while writing an article. We experience radiative heat transfer throughout the day, everyday. Tracking or calculating how much energy (ultraviolet, visible, or infrared) is radiated from one object to another is important to the design of a variety of things. Remote temperature sensors, night-vision cameras, missile systems, even buildings and landscapes, can be improved by controlling radiative transfer.

The basic relationship governing the radiative transfer between two small surfaces is simple. Simulating transfer between many, arbitrarily shaped objects, however, is not. Add a variety of surface treatments and the problem becomes even more challenging. Ray-trace software offers a relatively simple method for “tracing radiation” in such complex systems.

Ray tracing has been used in lens-design software since the 1960s to simulate the propagation of visible and invisible (UV and IR) light through optical systems. Rays are assigned power, position, and direction, then reflected, transmitted, and scattered between surfaces. Ultimately, the power and distribution of the rays incident on a given surface defines the radiative transfer to that surface. The principal advantage of this technique is that it can handle virtually any geometry. It does not require us to subdivide each surface into a predetermined number of segments, or to determine which surface segments are visible to other surface segments.

The principal drawback to calculating radiative transfer by ray tracing is that accuracy is limited by statistical noise resulting from the Monte-Carlo ray-trace approach. To improve accuracy we must trace more rays. Fortunately, we can overcome statistical noise by directing rays only to areas of interest and by taking advantage of the increased speed of today’s computers.

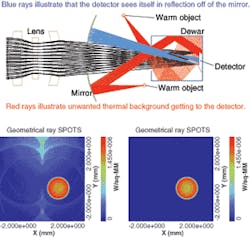
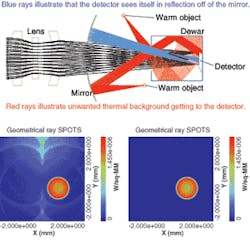
To illustrate simulating radiative transfer by ray tracing let’s first consider an IR imaging system, which measures the radiance or temperature of distant objects. To make IR sensors work it is essential to control the temperature and location of components within the sensor. For example, we placed a detector in a cooled Dewar (see Fig. 1, top). A warm spherical mirror limits the detector’s view of warm components. The Dewar and spherical mirror reduce the thermal background incident on the detector. Despite these conscious design features, warm objects that are not directly visible from the detector are visible in reflection off the Dewar walls and the spherical mirror. We used our Advanced Systems Analysis Program (ASAP) to identify and quantify these stray radiation paths by ray tracing.

The lens images a distant scene onto the cooled detector. Assume that the scene is simply a 293-K sphere with emissivity equal to 1. To demonstrate how unwanted radiation can degrade the image, we add two 293-K, emissivity-1 spherical objects, then calculate the irradiance (W/mm2) distribution at the detector for 8- to 12-µm radiation from both the scene and the unwanted noise sources (see Fig. 1, bottom left).

The thermal background comes from two paths: reflections from the inside the Dewar and reflection off the mirror to the Dewar then to the detector. To illustrate how scatter properties affect radiative transfer, we change the interior of the Dewar from specular to a machined metal finish (see Fig. 1, bottom right).

In the thermal-imager example we trace rays forward from warm sources to the detector. Forward ray tracing is efficient when sources and collectors are large or close together. When they are not we can also calculate radiative transfer by backward ray tracing. We have a choice between forward and backward ray tracing because of reciprocity in scattered light and symmetry between forward and reverse propagation.1

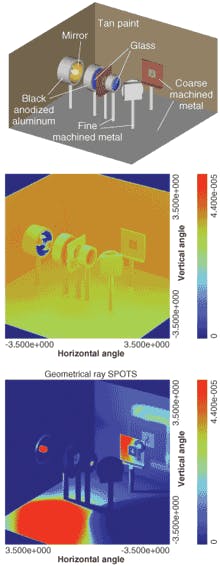
We apply both forward and backward ray-trace techniques in our second example: a simple projector system on a laboratory bench (see Fig. 2, top). In this lab setup, we illuminate an opaque slide by Kohler illumination and reimage that slide onto a second slide holder.2 Turn off the lights in the lab, turn off the lamp, and capture the IR radiative transfer from and between the parts on the lab bench (see Fig. 2, center). All of the parts are 293 K but their emissivities differ. For example, the anodized aluminum mounts have high emissivity while the mirrors and lenses have low emissivity. Now turn on the lamp and capture the radiative transfer at visible wavelengths (Fig. 2. bottom).

Complex geometry, numerous sources with arbitrary shapes, a variety of surface-scatter distributions-the laboratory bench simulation combines all of these challenges and demonstrates that we can simulate radiative transfer by ray tracing. With this approach we can accurately predict scene radiance for any ultraviolet, visible, or infrared waveband. Knowing whether there is too much or too little radiation is the first step to improving a design.

ACKNOWLEDGMENT

The author would like to thank Gary Peterson of Breault Research Organization for developing and teaching the ASAP techniques used in the simulations.

REFERENCES

1. G. L. Peterson, Discussions and internal memoranda, Breault Research Organization, Inc., 1995-2004.
2. U.S. Patent 1143287 (1915).

ROBERT PAGANO is a senior optical engineer at the Breault Research Organization, 6400 East Grant Rd., Suite 350, Tucson, AZ 85715; e-mail: [email protected].