Choosing software: Different design paths lead to different solutions, Part II
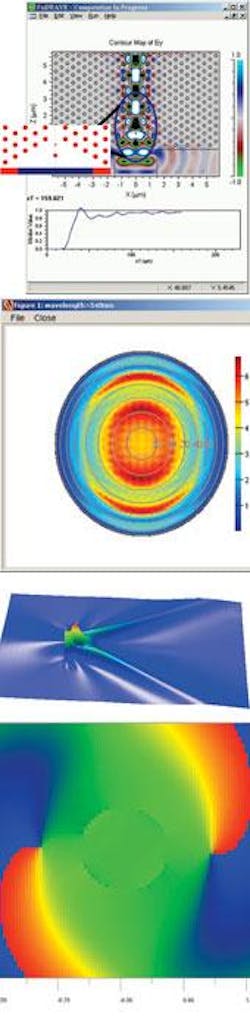
When the physical features of an optical system shrink to within an order of magnitude of the wavelength of light, physical-optics software must be used for system design, because the assumptions necessary for a geometrical optics or ray-tracing approach no longer hold. Part I of this series was published in September (see https://www.laserfocusworld.com/software-accessories/software/article/16555945/choosing-software-different-design-paths-lead-to-different-solutions-part-i). In this article, we look at a few algorithms commonly used in commercially available photonic-design software: finite-difference time-domain (FDTD) method, the finite-difference beam-propagation method (FD-BPM), and a couple of mode-solving methods.
Finite-difference methods
The FDTD technique is a discrete representation of Maxwell’s equations on a grid that is exact in the limit that the grid spacing goes to zero, so in principle FDTD can be used to solve any optical problem without approximation. Typical applications for optical software based on an FDTD algorithm include design of photonic-bandgap structures for photonic crystals, ring resonators, wavelength-scale object scattering (such as surface-plasmon effects), gratings and other diffractive structures, high-index-contrast waveguides, biosensing devices, and nano- and microlithography. In addition, all sorts of optical materials can be used with FDTD algorithms—a crucial factor because of the increasingly complex materials being incorporated into photonic component and system designs (see figure).
The primary limitation of FDTD is that it is computation intensive. In practice, FDTD needs to have about 15 to 20 grid points per wavelength in every direction, depending on the application and accuracy required. So a three-dimensional design problem with feature sizes on the order of one wavelength would require about 10,000 grid points, and the need to calculate the field for every grid point rapidly renders FDTD impractical for large devices.
The upper limit for using the FDTD approach without clustering computers is about 10 wavelengths. One source interviewed for this article offered an example of clustering on more than 1000 processors on West Grid, Western Canada’s largest supercomputer, for an almost 1000× improvement in computation speed. Different vendors take significantly different approaches to optimize the performance of their software in solving problems that require clustering. The approaches include parallel processing features in the software and, most recently, dedicated hardware to boost single system processing speeds.
For light propagating through a low-index-contrast waveguide or optical fiber, where it is appropriate to use the paraxial approximation, a finite-difference beam-propagation method (FD-BPM) can be used, which retains the finite difference grid in transverse directions but assumes a slowly varying envelope in the axial or propagation direction. Other beam-propagation methods exist, but the finite-difference version is most commonly used commercially. Finite-difference BPM can still solve some high-index-contrast problems and some problems with significant power off-axis, but the further one strays from safe cases the more is left to the skill and judgment of the user. The paraxial approximation enables BPM to analyze much longer structures (on the millimeter and centimeter scale) than would be reasonable for analysis with FDTD. Typical FD-BPM applications include WDM devices, switches, modulators, multimode interference devices, passive splitters, and design of standard and specialty fiber.
Modal methods
Modal solutions offer another approach to waveguide design problems. Just as plane waves are the natural “modes” of free space, modal analysis allows the user to determine the natural “modes” of a waveguide. Dispersion and loss of a plane wave is trivial in free space, but in a waveguide, modal dispersion and loss are not so trivial and depend on the details of the structure and the optical materials used. Unlike BPM and FDTD, which are grided methods that approximate the solution at a discrete set of points, mode-based solutions discretize in a different way by considering only a finite number of modes.
Eigenmode expansion (EME) provides a rigorous solution of Maxwell’s Equations but is also able to deal with very long structures. Finite-difference time-domain is entirely direction agnostic, while EME has a preferred direction that can be overridden by increasing control parameters. Also, while FDTD may need 20 grid points per wavelength in each direction and BPM may need only one grid point for every five wavelengths in the propagation direction, EME can propagate through a straight waveguide in one step, whether it is 1000 µm or 1000 m long. Waveguides with large cross sections place EME at a disadvantage, however. While EME computational time scales less rapidly than BPM in the direction of propagation it scales more rapidly in the transverse direction. Eigenmode expansion might be used for modeling challenging structures such as silicon-on-insulator waveguides or very long devices such as fiber tapers.
A special type of modal method, coupled-mode theory (CMT), tends to prove useful in applications such as coupling light propagating between different segments or components (between waveguides and gratings for instance). While CMT-based software might solve problems too big for either FDTD or BPM in a fraction of the time, CMT is only useful in specific situations, such as long periodic structures with variations that are not too strong. A specialist can look at these structures and determine whether the CMT is likely to give a good result. But like anything else, it cannot be used blindly.
Other mode-solving methods exist (one of them uses an FDTD Yee cell method to perform EME), as well as algorithms based on wave analysis and innumerable other methods. In addition, there are a whole raft of other algorithms that are used in academics, including integral-equation methods and Gaussian methods, and there is a lot more original research going on. The challenge is to create an algorithm that can do everything in a reasonable time frame.
Even with widespread and ongoing in-house research on new and improved algorithms, commercial vendors are still finding their business increasing. Design organizations tend to switch from using in-house to commercial software for benefits such as continually updated code, CAD compatibility, or graphical user interfaces that may not be feasible for them to develop or maintain in-house.
Considering the variety of approaches available, as mentioned in Part I of this article, there is no substitute for contacting several vendors to find the most appropriate solution for a particular problem. This is particularly true because it is not unusual for a problem to require a combination of approaches, which may also require compatibility with the ray-tracing software discussed in Part I of this article.❏
AUTHOR’S NOTE
The information in this article is based on interviews with four commercial providers of photonic-design software (in alphabetical order): Lumerical Solutions (Vancouver, British Columbia, Canada), Optiwave Systems (Ottawa, Ontario, Canada), Photon Design (Oxford, United Kingdom), and RSoft Design Group (Ossining, NY). They can be found online at www.lumerical.com, www.optiwave.com, www.photond.com, and www.rsoftdesign.com.
About the Author
Hassaun A. Jones-Bey
Senior Editor and Freelance Writer
Hassaun A. Jones-Bey was a senior editor and then freelance writer for Laser Focus World.