Filtering techniques eliminate Gaussian image noise
Noisy images create problems in machine vision applications. Spatial filtering methods for removing noise have existed for more than a decade, but face problems like over smoothing without any preservation of edges, gradient reversal artifacts, ringing artifacts, and shift variance.
For machine vision and imaging tasks, the first step in finding eventual success is getting the highly informative image. Many types of noise exist, including salt and pepper noise, impulse noise, and speckle noise, but Gaussian noise is the most common type found in digital imaging. Within digital imaging, Gaussian noise occurs as a result of sensor limitations during image acquisition under low-light conditions, which make it difficult for the visible light sensors to efficiently capture details of the scene (see Fig. 1).
Mathematically, Gaussian noise can be characterized by the equation of the bivariate circular Gaussian function as:Newer filtering methods like block-matching and 3D filtering (BM3D), nonlinear means (NLM) filtering, and Shearlet transform prove more effective than previous methods used to remove noise. Spatial filtering techniques modify the spatial features of an image. A spatial filtering kernel helps facilitate spatial filter implementation. Convolution of a smoothing kernel with the desired noisy images produces a denoised image. Based on the property of these kernels, different denoising results can be obtained. For example, a Gaussian kernel is obtained by plugging in different space values for x and y into the equation,1 and by controlling the value of sigma, the degree of smoothing can also be controlled.
Uniform image smoothing represents the main problem encountered with primitive filters, as doing so results in compromised important details.8 Introducing range parameters into the Gaussian equation helps avoid the smoothing operation at the edges and contours and thus solve the problem. Using this filter—a bilateral filter9—introduces artifacts into the resulting image. However, a guided filter offers a more effective, edge aware spatial filtering approach. This filter uses a guidance image to effectively smooth consistent pixel intensity areas while retaining important detail information with the help of a guidance image. This filter is effective in removing artifacts.10 Another filter effective in removing artifacts while preserving semantically meaningful information is the anisotropic diffusion filter, which uses second order partial differential equations with necessary parametric variations for smoothing.7
On the other hand, transforms use orthonormal filter banks to decompose images into low frequency and high frequency sub-band images. The low-frequency information contains the uniform pixel intensity areas and high frequency information contains all the edges and contours present in the image. A transform is considered effective in separating information if it can extract edges and contours out of multiple directions in the image. For example, a wavelet transform extracts high frequency information in three directions—horizontal, vertical, and diagonal—whereas the Shearlet transform extracts information in multiple directions.
Gaussian noise affects higher frequencies. Applying a thresholding operation to high frequency (detail) sub-bands eliminates noise. As transforming an image takes it into another domain, coefficients are obtained as a result. To retrieve original pixel intensities, inverse transform applies to these modified coefficients, a process that lays down the complete picture of denoising more comprehensively because of its information separation strategy.2, 11
NLM filtering, weighted least square (WLS) filter, and BM3D filtering represent more sophisticated strategies for achieving better results. In WLS filtering, the weighted least square energy function is minimized to obtain the output, so in this strategy, recursive filtering applies to the noisy image. This filter is fast and effective in removing halo artifacts.13 NLM filters prove more effective in removing the outliers and mainly, shot noise. The nonlinearity of these filters helps to effectively remove the background noise while preserving meaningful information.8
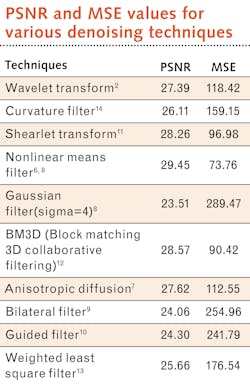
BM3D algorithms group fragments of images based on their similarity (block matching) and filter every fragment.12 The BM3D approach is a very effective approach, with the smallest computational load.For experimentation, a mobile device camera with dual camera setup with 12 Mpixel camera sensor and 13 Mpixel depth sensor for emphasizing objects in a scene provides images. Images in Figure 3 show the results of a standard image of a house contaminated by Gaussian noise of different standard deviation (sigma). In this experiment, images with Gaussian noise with sigma 30 are used. When higher sigma noise is added, the image gets more distorted and more difficult to recover (see Fig. 5). For testing, the two most popular and widely used metrics evaluate the performance: peak signal-to-noise ratio (PSNR) and mean square error (MSE): The two metrics can be explained as follows:
a) MSE: The square of difference between the pixel values of the original image and denoised image is known as MSE. The MSE of a denoised image IDwith dimensions M × Nwith respect to the original image Iocan be written mathematically as5The higher the MSE value, the lower the denoised image quality. Hence, lower value of MSE indicates good denoising technique performance.
b) PSNR: Measure of signal power compared to noise power. The higher the ratio, the higher the visual quality of the image. Mathematically, it can be written as:5When compared to the original image, the visual results tend to lose some details, but the freedom of choosing parameters for the degree or smoothing provides flexibility for using these techniques in disparate applications.
Several spatial filtering techniques can remove Gaussian noise. Additionally, some transform techniques can also remove noise from images. Spatial filters do not break the image into its high and low frequency components but apply directly to an image to modify pixels spatially to remove the noise (see Fig. 3). Transforms first break an image into scales of low and high frequency information (multiscale decomposition, or MSD), then a thresholding operation applies to various components and an inverse transform is applied to recover a noise-free image (see Fig. 4).Noise impacts the higher frequencies of an image, so the thresholding operation is only applied to the high-frequency layers. All spatial filters employed to remove noise remove higher frequencies present in the image. As the important edge and contour information is also high frequency information, a spatial filter or transform must remove noise without affecting the relevant edges and contours. All spatial filters or transforms proposed through the years have tried to solve this problem,3-5 but BM3D, nonlinear means filter, and Shearlet transform perform best.
REFERENCES
1. F. Russo, IEEE Trans. Instrum. Meas., 52, 4, 1148–1154 (2003).
2. A. Vermaa and A. Shrey, Image Denoising in Wavelet Domain, 1–10.
3. R. M. Sairam, S. Sharma, and K. Gupta, J. Eng. Sci. Tech. Rev., 8, 5, 41–48 (2013).
4. R. C. Gonzalez and R. E. Woods, Digital Image Processing, 2 (2007).
5. B. Goyal, A. Dogra, S. Agrawal, B. S. Sohi, and A. Sharma, Inform. Fusion, 55, 220–244 (2020).
6. L. G. Shapiro and G. C. Stockman, Computer Vision, Prentice-Hall (2001).
7. P. Perona and J. Malik, IEEE Trans. Pattern Anal. Mach. Intell., 12, 7, 629–639 (1990).
8. L. Shao, R. Yan, X. Li, and Y. Liu, IEEE Trans. Cybern., 44, 7, 1001–1013 (2014).
9. C. Tomasi and R. Manduchi, “Bilateral filtering for gray and color images,” Sixth International Conference on Computer Vision, 839–846 (1998).
10. K. He, J. Sun, and X. Tang, “Guided image filtering,” European Conference on Computer Vision, 1–14 (2010).
11. G. Easley, D. Labate, and W.-Q. Lim, Appl. Comput. Harmon. Anal., 25, 1, 25–46 (Jul. 2008).
12. K. Dabov, A. Foi, V. Katkovnik, and K. Egiazarian, IEEE Trans. Image Process., 16, 8, 2080–2095 (2007).
13. M. A. Rahman, P. K. Dash, and E. R. Downton, IEEE Trans. Power App. Syst., 11, 4204–4210 (1982).
14. A. I. El-Fallah and G. E. Ford, “The evolution of mean curvature in image filtering,” Proc. 1st Int. Conf. Image Process., 1, 298–302 (Nov. 1994).
15. See https://bit.ly/MathworksRef15.
About the Author
Ayush Dogra
Assistant Professor - Senior Grade, Chitkara University Institute of Engineering and Technology
Dr. Ayush Dogra is an assistant professor (research) - senior grade at Chitkara University Institute of Engineering and Technology (Chitkara University; Punjab, India).
Apoorav Maulik Sharma
Research Fellow, Department of Electronics & Communication Engineering (ECE)
Apoorav Maulik Sharma is a research fellow in the Department of Electronics & Communication Engineering (ECE) in the University Institute of Engineering & Technology (UIET) at Panjab University (Chandigarh, India).
Bhawna Goyal
Assistant Professor, UCRD and ECE departments at Chandigarh University
Dr. Bhawna Goyal is an assistant professor in the UCRD and ECE department at Chandigarh University (Punjab, India), and in the Faculty of Engineering at Sohar University (Sohar, Oman).
Sunil Agrawal
Professor and Coordinator, Department of Electronics & Communication Engineering (ECE)
Sunil Agrawal is professor and coordinator in the Department of Electronics & Communication Engineering (ECE) in the University Institute of Engineering & Technology (UIET) at Panjab University (Chandigarh, India).
Renu Vig
Professor, Department of Electronics & Communication Engineering (ECE)
Renu Vig is a professor in the Department of Electronics & Communication Engineering (ECE) in the University Institute of Engineering & Technology (UIET) at Panjab University (Chandigarh, India).

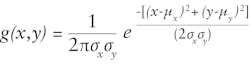
![FIGURE 2. The graph shows variation in value of function according to the value of sigma (standard deviation) with fixed mean (μ=0) [4]. FIGURE 2. The graph shows variation in value of function according to the value of sigma (standard deviation) with fixed mean (μ=0) [4].](https://img.laserfocusworld.com/files/base/ebm/lfw/image/2020/05/2005LFW_dog_z02.5eb17dee887d8.png?auto=format,compress&fit=max&q=45?w=250&width=250)
![FIGURE 3. Spatial parametric filtering is applied [4]. FIGURE 3. Spatial parametric filtering is applied [4].](https://img.laserfocusworld.com/files/base/ebm/lfw/image/2020/05/2005LFW_dog_z03.5eb18043b0b21.png?auto=format,compress&fit=max&q=45?w=250&width=250)
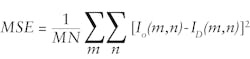



![FIGURE 4. A transform denoising process is applied [3, 4, 11]. FIGURE 4. A transform denoising process is applied [3, 4, 11].](https://img.laserfocusworld.com/files/base/ebm/lfw/image/2020/05/2005LFW_dog_z04.5eb180a63f294.png?auto=format,compress&fit=max&q=45?w=250&width=250)