Simplex algorithm aligns quickly and simply

RONG ZHANG and FRANK G. SHI

The packaging of fiberoptic devices is the most expensive part of the manufacturing process, presenting challenges to engineers working to reduce costs. A particularly difficult packaging step is the alignment of a light source and its receiving fiber. An efficient and robust alignment algorithm for locating the optimal fiberoptic coupling position is critical to an efficient packaging of fiberoptic components and modules.

Conventional methods

The most frequently used fiberoptic-alignment routines consist of two sequential steps: a coarse and a fine alignment. The object of the first (coarse) alignment step is simply for the fiber to catch the “first light” from the laser diode. This step is often accomplished by spiral or square scanning and machine-vision methods. After finding first light, the laser-to-fiber coupling position needs to be further adjusted in the second (fine) alignment step to obtain the maximum optical-coupling power.

The hill-climbing algorithm, which was developed from a “gradient-search” algorithm used for general x-y-z axial alignment, has been widely adopted as a fine-alignment method for current photonics packaging technology.¹ But the inherent limits of this algorithm cause some disadvantages in practical applications. First, because the hill-climbing method is a one-dimensional gradient-searching method, it can only deal with the alignment in one direction at a time, usually requiring on the order of 120 to 140 measurements to locate the peak in a two-dimensional (2-D) plane.² Second, this approach works well if the light output is a perfect Gaussian profile; however, in the case of multiple suboptimal peaks in the alignment plane, often the algorithm traps into a false peak. Third, because of the low signal-to-noise ratio at low power levels, hill climbing usually requires coarse alignment to reach a high-threshold power reading before it can perform successfully, thus consuming more time.

The simplex approach

The concept of the basic “simplex” method was first proposed in 1962 (a simplex is the N-dimensional version of a triangle; for example, a 3-simplex is a tetrahedron).³ The simplex method produces a numerical solution to a multidimensional problem. In it, a geometric simplex is constructed from (N + 1) vertices and sides of fixed length; the surface of the so-called objective function is explored by means of sequential reflections of the worst vertices, causing the center of the successive simplexes to move toward the maximum.

As a result of the fixed lateral length of the simplex, this algorithm exhibits a rather slow convergence or low accuracy. To overcome these shortcomings, the modified or variable-size simplex method was developed.⁴ Although this method has been widely applied in various fields as a promising optimization tool, its application in fiberoptic alignment has only recently been demonstrated by our group.⁵ Using simulation, we have demonstrated that the new method, the modified simplex method (MSM), is five times faster than the hill-climbing method in locating the optimal fiberoptic coupling position, and it works well for alignment of up to six axes, as well as for the alignment of multichannel-array devices and in the presence of multiple modes. We also demonstrated that the selection of the initial simplex size is important to the success of the method. An experiment has now been done that demonstrates the effectiveness of this new method in a simple 2-D alignment case.

Experimental comparison

The devices under test were two single-mode-fiber arrays. Because the purpose of this work as a first step was to demonstrate the effectiveness of the algorithm, only the alignment of the first channel of each fiber array in a 2-D plane was considered. The experiment was conducted on a motor-actuated alignment workstation (see Fig. 1).

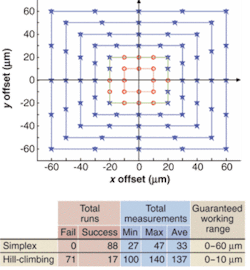
For the purpose of comparing the performance of our algorithm to the hill-climbing algorithm that was originally integrated in the commercial workstation, we first conducted a time-consuming x-y planar full-scan. A regular Gaussian distribution of optical power was observed, helping us to easily locate the optimal alignment position of peak power output. We then added arbitrary offsets in both the x and y directions and started the two algorithms from the same designated position, producing a fail/succeed distribution map of the two algorithms based on 88 different starting positions (see Fig. 2 and associated table).

FIGURE 2. A new simplex fiber-alignment algorithm was experimentally compared to a conventional hill-climbing algorithm at 88 starting positions. The stars show the testing points where hill-climbing failed to locate the peak, while the open circles show the testing points where both the hill-climbing and simplex methods found the peak. While the hill-climbing algorithm failed even at one-third the peak intensity, the simplex algorithm quickly located the peak over a large region with an average of 33 movements and power readings.

The guaranteed working range for MSM is 0 to 60 µm, a sixfold increase over that for the hill-climbing algorithm. Actually, as long as the offset is greater than 40 µm, the misalignment can clearly be seen by eye. Under this situation of 40 µm or greater lateral misalignment, the hill-climbing method requires a lengthy spiral or square-scanning-type coarse alignment to bring the fiber tip within a 0- to 10-µm range before we can actually apply the algorithm. With MSM, however, this coarse-alignment step can be eliminated, dramatically reducing alignment-cycle time.

Side modes

To test the algorithm with the presence of side modes, we moved the right-side stage in the setup a distance of 30 µm along the z axis to increase the separation between the two fiber arrays. The 2‑D optical-power intensity profile within offsets of x = y = ±30 µm, a multipeak plane is clearly present. We started both the hill-climbing algorithm and MSM at the same randomly picked positions (see Fig. 3). By using MSM, the 2-D profile of the aligned optical power versus x and y offsets shows that the real peak was located. When using the hill-climbing technique, the device under alignment traps into a fault peak reading less than 3-µW optical power. This experiment demonstrates that the simplex method can locate the real peak of a suboptimal beam while the hill-climbing approach cannot.

FIGURE 3. A test was done on a suboptimal beam with a multipeak profile (top). Using MSM, a 2-D profile of the aligned optical power versus x and y offsets shows that the real peak was located (center), while only a fault peak with a reading of less than 3-µW optical power was located by the hill-climbing algorithm (bottom).

The MSM method is more than ten times faster than the conventional approach. It also reduces the long cycle needed for the coarse-alignment step and elimates the expensive machine vision tools for fine alignment. Moreover, MSM is failure-proof (by avoiding trapping into fault peaks). Thus, this new technology is expected to significantly reduce the cost of manufacturing optical devices that involve optical alignment.

REFERENCES

1. C. Gabler et al., SPIE Integration and Packaging of Optoelectronic Devices 703, 8 (1987).
2. Z. Tang et al., Fiberoptics Communications 196(1-6) 173 (2001).
3. W. Spendley et al., Technometrics, 4, 441 (1962).
4. J. A. Nelder and R. Mead, Computer J. 7, 308 (1965).
5. R. Zhang and F. G. Shi, IEEE Trans. Advanced Packaging 27, 173 (2004).

Rong Zhang is a postdoctoral researcher at Beckman Laser Institute, University of California, Irvine; Frank G. Shi, who directs the OptoElectronics Packaging Lab, is professor in the materials science, chemical engineering, and electrical engineering departments of the University of California, Irvine; Irvine CA 92697; e-mail: [email protected].