Distributed tuned mass damping quiets vibrations

JEFFREY A. ZAPFE

Optical tables are typically used in applications in which even small deflections of the working surface (static and dynamic) cannot be tolerated. In modern optical tables, sandwich construction techniques produce a structure with a very high stiffness-to-weight ratio. The most common table configurations use stainless-steel facesheets with a steel honeycomb core. Conventional damping techniques used to attenuate a table's vibration modes can reduce its performance at other frequencies.

Kinetic Systems Inc. (KSI; Boston, MA) has developed an alternate vibration-suppression approach, distributed tuned mass damping, that effectively suppresses fundamental-mode table vibration without degrading performance at other frequencies. The company is currently in preproduction on a commercial line of tables featuring the new technique.

Like all physical bodies, optical tables have resonant vibration modes. The high stiffness-to-weight ratio causes the first resonant frequencies of modern optical tables to be much higher than earlier solid granite tables. The first two vibration modes of an optical table are usually the first bending mode and the first torsion mode. The order of the two modes is dependent on the aspect ratio (length to width) of the table. Below an aspect ratio of 2:1, the torsion mode is usually the lowest in frequency, while above 2:1 the bending mode is typically lower frequency.

Soft pneumatic mounts isolate the tables from excitation caused by floor vibration, providing better than 99% isolation at 20 Hz. The first resonant frequency of a table is typically in excess of 150 Hz, however, so vibration problems are more likely to stem from equipment mounted on the table or from disturbances acoustically coupled through the air.

Tuned mass damping

The metallic construction of an optical table provides minimal inherent material damping, so the finished product can exhibit strong resonant responses. Tuned mass inertial dampers (TMDs) offer one method for controlling this response, providing a lightweight, effective damping treatment that can be easily tuned to address a specific frequency. A TMD consists of a spring (steel bar) and a mass that can be tuned to the resonant frequency of the table. Typically, a TMD will be placed in two to four of the corners of a table. When coupled, the damper and table behave like two out-of-phase oscillators, producing a net cancellation of the response at the resonant frequency. The damper/table coupling does have the effect of introducing two new resonant modes into the system, but the magnitude of the response at each resonance is generally smaller than that of the initial peak.

Tuned mass dampers are effective over a narrow bandwidth; because the modal frequencies of the undamped table fluctuate as a result of normal manufacturing variations, the devices must be specifically tuned for each table by adjusting the mass or spring stiffness. The effective damping bandwidth of a single TMD can be broadened somewhat by dissipating energy from the spring/mass system. A powerful method for broadening the damping bandwidth is to combine a number of TMDs, each tuned to a slightly different frequency, into a distributed system.

Previous research has concentrated on dampers distributed either spatially or in frequency. A newer method combines the two, distributing the TMDs in both position and in frequency.1 A system of distributed tuned mass dampers (DTMDs) can attenuate all modes within the design band of frequencies. It is also extremely tolerant of variations in the dynamics of the table, so manufacturers can eliminate the time-consuming step of tuning the dampers on each table.

To demonstrate the effectiveness of the DTMD approach, our engineering group at KSI compared the dynamic response of an undamped optical table to the same table damped with discrete TMDs and with DTMDs. In the DTMD, a large number of individual TMDs (up to several hundred) are applied to the table. Small adjustments in the masses of the individual TMDs tune each to a slightly different frequency. The natural frequencies of the dampers cover a specific frequency band that includes the table resonances of interest.

To determine the design band, we use a finite element model, defining the DTMD as a uniform, distributed surface with an area density possessing a frequency-dependent magnitude and phase. The distribution of damper frequencies within the design band determines the effective mass of the DTMD. At low frequency, this is simply equal to the physical mass of the collective absorbers. At frequencies within the design band, because some dampers are being driven near resonance, the effective mass of the DTMD can exceed its physical mass by many times.

Within the design band of the DTMD used in our study, for example, the effective mass exceeds the physical mass by 2.5 times. In addition, the effective mass has a nonzero phase angle, which means the DTMD can dissipate energy from the optical table. We arranged the distribution of individual dampers to produce a relatively flat, effective mass magnitude over the design band. More recently, we have determined that a low-frequency-weighted effective mass distribution can be equally as effective.

Experimental verification

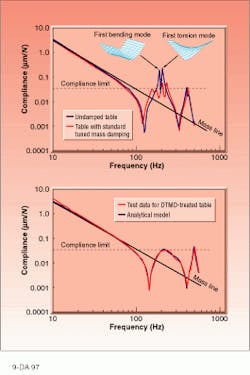
For the actual demonstration, we used a standard KSI optical table measuring 243.8 × 121.9 × 20.3 cm (8 ft × 4 ft × 8 in.) and evaluated table dynamics using a compliance measurement. Compliance is the ratio of dynamic displacement to applied force at a specific point on the table—in this case, we applied the impulse at a corner of the table with an instrumented force hammer, recording the disturbance with an accelerometer and running the data through a Fourier analyzer. The corner excitation allowed us to capture both the bending and torsion modes of the table (see figure).

Corner compliance—the ratio of dynamic displacement to force applied at the corner of an optical table—shows that discrete tuned mass dampers (TMDs) introduced to suppress bending and torsion mode vibration produce smaller secondary peaks at other frequencies (top). The spurious peaks can be addressed with additional discrete dampers, but this would increase the complexity and cost of the damping operation. A system of tuned mass dampers distributed in frequency and in position across the surface of an optical table can suppress both bending and torsional vibration below desired limits without introducing spurious vibrational frequencies (bottom).

For the undamped table, the two lowest table resonances were the first bending mode at 190 Hz and the first torsion mode at 208 Hz. We applied a conventional discrete TMD system to the table; discrete dampers introduced additional degrees of freedom into the table's dynamics, transforming the table's first two resonant peaks into four smaller peaks, the first two of which fell below the specified compliance limit. Additional discrete dampers could address the two peaks still above the limit, but this would increase the complexity and cost of the damping operation.

We next treated the table with a highly distributed system. Approximately 300 TMDs were applied to the surface of the optical table, concentrated in a 1- to 2-sq ft region around the corners of the table (see photo at top of this page); in production, the dampers will be located internally where they will be invisible to the user. For the comparison exercise, the design band ranged from 150 to 300 Hz, and the damper masses ranged from 60 to 230 g. The physical mass of the DTMD was 25 kg, which was comparable to the mass of the discrete TMDs in the standard treatment.

The DTMD system successfully attenuated both modes (bending and torsion) within the design band, driving both below the compliance limit. Unlike the standard treatment, the DTMD created no residual modes. A second system consisting of a 37-kg DTMD reduced peak compliance by another 8%.

The DTMD minimizes all vibrational modes within the desired frequency band, whereas discrete tuned dampers do not generally provide sufficient flexibility to address multiple modes. From a production standpoint, the technique simplifies the manufacturing process by eliminating the time-consuming tuning step. The versatility of the DTMD also introduces some interesting design possibilities, such as the ability to produce a system that damps vibration over a specific frequency band that might be particularly sensitive for an end user.

Kinetic Systems plans to offer optical tables with DTMD systems in the near future. It is currently in the preproduction stages, designing systems with 50 to 60 dampers. The dampers will be classified by weight and applied without any additional tuning. The tables are expected to be commercially available by early 1998.

REFERENCE

1. J. A. Zapfe and G. A. Lesieutre, AIAA Journal 35 (4), 753 (1997).