Nonlinear Optics: Engineered metaoptics forge new nonlinear devices
YURI KIVSHAR
Nanophotonics describes the subwavelength localization of light, and it is usually associated with plasmonics. However, the emerging field of optically resonant dielectric nanophotonics provides novel research directions for nanoscale optics.1 All-dielectric resonant nanophotonics use subwavelength Mie-resonant (or particle morphology-dependent) dielectric nanoparticles as elementary units (or “meta-atoms”) for creating highly efficient optical metadevices.
Whether called metamaterial-based optics or metaoptics, the unique optical resonances of these engineered nanoscale structures are accompanied by strong localization of both electric and magnetic fields, and they are expected to replace different plasmonic components in a range of potential applications. Importantly, resonant dielectric structures can lead to many novel effects originating from interference of several modes.
Optical cavities and Mie resonances
One of the key targets for making a successful laser is to confine light in an optical cavity. A conventional optical cavity traps light by using real or effective mirrors and using the physics of total internal reflection or scattering from periodic microstructures such as photonic crystals. Trapping in all such systems is characterized by the quality factor (Q factor)—a measure of the efficiency of the reflecting boundaries—being weakly dependent on the cavity geometry.
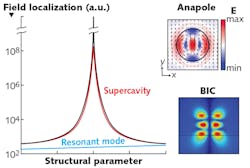
But recent advances in metaoptics based on Mie resonances on high-index dielectric structures suggest an alternative way to confine light by using nonradiating optical states such as anapoles or bound states in the continuum that can induce large subwavelength field enhancements at the nanoscale that are crucially dependent on system geometry (see Fig. 1).2, 3
Of primary importance is that these isolated dielectric nanoparticles with simple geometries can support both electric- and magnetic-type resonances of comparable strengths. A strong magnetic dipole resonance occurs due to a coupling of incoming light to the circular displacement currents of the electric field, owing to the field penetration and phase retardation inside the particle. This occurs when the wavelength inside the high-index material of the particle becomes comparable to the particle’s spatial dimension—namely, 2R is approximately λ/n, where n is the refractive index of the particle’s material, R is the nanoparticle’s radius, and λis the wavelength of light.
This is a type of geometric resonance that requires the nanoparticle to have a large refractive index to support strong magnetic-dipole resonances in the subwavelength regime. Similarly, a dielectric nanoparticle can support resonances dominated by the electric dipole and other high-order multipoles such as electric quadrupole and magnetic quadrupole resonances. The Mie resonances are usually associated with localization of the incident electromagnetic field inside the particles, suggesting at least two-orders-of-magnitude enhancement of many optical effects observed with high-index dielectric nanoparticles compared to nonresonant cases.1
Supercavities: Anapoles and bound states in the continuum
The term anapole means “without poles” and was originally proposed in the late 1950s by Yakov Zeldovich to model elementary particles that do not interact with the electromagnetic fields.4 Anapole states have been investigated in astrophysics, as they could explain the origin and composition of dark matter in the universe within the parameters of classical physics.
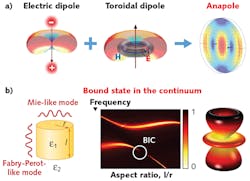
In the context of nonradiating sources, the theory developed during the 1990s demonstrated that different types of nonradiating states could be generated by combining classical electric and magnetic dipole modes with electromagnetic toroidal multipoles in configurations where the angular distribution of the energy density has the same and opposite parities. The simplest of these configurations is created by a toroidal dipole mode oscillating out of phase with respect to a single electric dipole.2
It was noted that such a particular interfering state—the superposition of an electric dipole and toroidal dipole modes—forms a simple but nontrivial nonradiating point source, later recognized as an elementary dynamic anapole state (see Fig. 2). A special feature of these two dipoles is that their far-field distribution is identical. For a particular set of parameters, these two dipoles can completely cancel each other by destructive interference in the far-field region when oscillating out of phase, hence creating a (weakly radiating) anapole.
Bound states in the continuum (BICs) originate from strong coupling between the modes in dielectric structures such as photonic crystals, metasurfaces, and isolated resonators. These BIC solutions were introduced in quantum mechanics 90 years ago by J. von Neuman and P. Wigner,5 while in photonics they were rediscovered only a few years ago.
A true BIC is a mathematical object with an infinite value of the Q factor and vanishing resonance width, and it can exist only in ideal lossless infinite structures or for extreme values of parameters. In practice, a quasi-BIC can be realized as a supercavity mode when both the Q factor and resonance width remain finite and approach the mathematical condition of a BIC asymptotically.
Recent discoveries6 reveal that even a single subwavelength resonator made of a high-index dielectric can be tuned into the regime of a supercavity mode supporting quasi-BICs (see Fig. 2). This can be achieved by varying the geometrical parameters of a nanoparticle when the radiative losses are almost suppressed due to destructive interference of leaky modes.
A new era of nonlinear nanophotonics
A large enhancement of the Q factor of high-index dielectric nanoscale resonators, with the parameters tuned to the supercavity conditions, offers a paradigm shift in nonlinear optics through the development of nonlinear metadevices.
The reason is that nonlinear optics at the nanoscale are governed by strong field confinement and resonant response not limited by phase matching. As a result, the processes of high-order harmonic generation can be boosted dramatically since they scale as (Q/V)n, where n is the process order and V is the mode volume. Therefore, a giant increase of the generation efficiency is expected in isolated subwavelength nanoparticles, as was recently predicted for second-harmonic generation (SHG) in aluminum gallium arsenide (AlGaAs) nanodisks.7
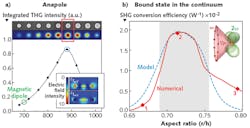
The first approach exploiting the anapole state to enhance nonlinear harmonic generation was demonstrated for germanium nanodisks (of 100 nm of thickness and radii ranging from 250 to 500 nm) by Grinblat and colleagues (see Fig. 3).8 When excited in the vicinity of the anapole resonance and taking advantage of a high field confinement, this structure performed a third-harmonic conversion from incident infrared light (1650 nm) into green light (550 nm) with an efficiency that is orders of magnitude higher than a flat structure.
Recently, a team at the Australian National University predicted and demonstrated the enhancement of the SHG efficiency for individual dielectric nanodisks in the quasi-BIC regime.
In the team’s experiments, the resonator is excited by an azimuthally polarized Gaussian beam providing perfect mode matching with the high-Q resonance, whose electric field is uniform with respect to the azimuthal direction, assuming a diffraction-limited beam waist and the value of the second-order nonlinear susceptibility of 290 pm/V. Both theoretical proposals7 and experimental observations on quasi-BIC nonlinear nanoparticles demonstrate breakthrough conversion efficiencies9 on the order of 10-3 W-1 (see table).
In the recent past, nonlinear nanophotonics was dominated by metallic nanoparticles. Metals were an attractive choice due to their extremely high intrinsic nonlinearities. In addition, the support of plasmon resonances allowed for light confinement and local intensity enhancement near electric-field hot spots. However, the overall efficiency of the nonlinear frequency conversion in plasmonic nanostructures remained very small—on the order of 10−10 W-1.
Conversion efficiencies in nanophotonics are usually limited by losses, small mode volumes confined to metal surfaces, and low laser damage thresholds. But all-dielectric nanostructures with Mie resonances provide an important pathway to enhance the nonlinear efficiency beyond the limits associated with plasmonics—approaching 10-6 W-1. These values can be pushed much higher to almost 10-2 W-1 with the concept of supercavities (see table).In summary, resonant dielectric nanostructures provide an alternative solution to enhance the performance of many nanophotonic devices that used metallic elements and plasmonic effects in the past. The study of resonant dielectric metaoptics has become a new research direction in metamaterials and nanophotonics, and it is expected to complement or substitute some of the plasmonic components in a range of potential applications.
The unique low-loss resonant behavior of engineered metaoptics makes it possible to reproduce many subwavelength resonant effects already demonstrated in nanoscale plasmonics without essential energy dissipation and, in addition, brings many novel concepts to practical applications. We anticipate that the novel physics of nonradiating optical states originating from the 90-year-old concept of BICs and enhanced by the recent discovery of optical anapoles will provide a new twist for both active and nonlinear nanophotonics.
ACKNOWLEDGEMENTS
The author thanks many of his colleagues and students for useful collaboration—he is especially indebted to Andrea Fratalocchi, Kirill Koshelev, Sergey Kruk, Mikhail Rybin, and Daria Smirnova. He also acknowledges financial support from the Strategic Fund of the Australian National University.
REFERENCES
1. S. Kruk and Y. Kivshar, ACS Photonics, 4, 11, 2638–2649 (2017).
2. K. Baryshnikova et al., Adv. Opt. Mater., 7, 1801350 (2019); https://doi.org/10.1002/adom.201801350.
3. K. Koshelev, A. Bogdanov, and Y. Kivshar, Sci. Bull., 64 (2019); https://doi.org/10.1016/j.scib.2018.12.003.
4. Y. B. Zeldovich, J. Exp. Theor. Phys., 6, 1184 (1958).
5. J. von Neuman and P. Wigner, Phys. Z., 30, 467–470 (1929).
6. M. V. Rybin et al., Phys. Rev. Lett., 119, 243901 (2017).
7. L. Carletti et al., Phys. Rev. Lett., 121, 033903 (2018).
8. G. Grinblat et al., Nano Lett., 16, 7, 4635–4640 (2016).
9. S. Kruk et al., 7th NANOMETA 2019, paper FRI4f.35, Seefeld, Austria (2019).
10. S. Kruk et al, Nano Lett., 17, 6, 3914–3918 (2017).
Yuri Kivshar is distinguished professor of The Australian National University (ANU), Canberra, Australia; e-mail: [email protected]; www.anu.edu.au.