Superlenses are nearsighted
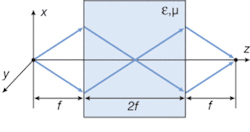
Materials with negative dielectric permittivity and negative magnetic permeability, also known as left-handed materials, and materials with negative refractive index have stirred much interest and controversy during the last few years. One of the primary sources of interest and controversy has been the possibility of creating an aberration-free “superlens” providing subwavelength resolution in the far field, constructed simply of a rectangular slab having permittivity and permeability of −1 (see figure).
The interest was so great that in 2003-just three years after John Pendry at Imperial College (London, England) proposed the idea, and David Smith, Sheldon Schultz, and colleagues at the University of California-San Diego actually created metamaterials yielding negative refraction at microwave frequencies-more than 100 research groups around the world were said to be working on metamaterials, and DARPA (the Defense Advanced Research Projects Agency; Arlington, VA) was sponsoring the first Negative Index Metamaterials Workshop.1, 2, 3
Voices of disbelief were raised, but positive research results were widely reported. In 2002, Prashant Valanju and colleagues at the University of Texas in Austin argued that negative refraction would violate the fundamental limit of the speed of light. And in the same year, Nicolas Garcia and Manuel Nieto-Vesperinas at the Spanish Council for Scientific Research (CSIC; Madrid, Spain) argued that an actual superlens would not be possible to construct due to the degradation of amplified evanescent waves by light absorption within the lens material.4, 5
An analytical expression describing the resolution limits of a superlens, published this month by Victor Podolskiy and Evgenii Narimanov at Princeton University (Princeton, NJ), suggests that all parties on both sides of the superlens controversy are partially right. Construction of actual superlenses is certainly possible, according to Podolskiy and Narimanov, but superlenses in the real world, like the 1950s cartoon character Mr. Magoo, would be extremely nearsighted. “Although the near-field performance of the superlens is encouraging, far-field subwavelength resolution is practically unachievable with current techniques,” according to Podolskiy and Narimanov.6
They explain that magnitude distortion in a propagating light pulse is caused by the exponential decay of the evanescent (“tending to vanish”) components of the wave vectors that carry subwavelength information. Conventional optics can correct for skewing of wave-vector-component orientation due to phase distortion, but not for the loss of subwavelength information due to magnitude distortion. In theory the superlens could correct for both, but the analytical expression derived by the Princeton team indicates that the resolution limit of the superlens would be about the same as the near-field resolution limit of conventional optics. So the superlens would definitely outperform the conventional lens, but only in the subwavelength near field.
REFERENCES
1. J. B. Pendry, Phys. Rev. Lett. 85(18) 3966 (Oct. 30, 2000).
2. D. R. Smith et al., Phys. Rev. Lett. 84(18) 4184 (May 1, 2000).
3. G. Marsh, Materials Today 6(1) 18 (January 2003).
4. P. M. Valanju et al., Phys. Rev. Lett. 88(18) 7401 (May 6, 2002).
5. N. Garcia and M. Nieto-Vesperinas, Phys. Rev. Lett. 88(20) 7403 (May 20, 2002).
6. V. A. Podolskiy and E. E. Narimanov, Optics Letters30(1) 75 (Jan. 1, 2005).