Ultrafast dips into the attosecond range
With the use of chirped-phase mirrors to reduce dispersion, and carrier-envelope phase stabilization to control the waveform, ultrafast lasers allow the generation of subfemtosecond pulses.
In 1981, Charles Shank and coworkers at Bell Labs (Murray Hill, NJ) redefined the term “ultrafast” when they reported the demonstration of subpicosecond pulses from a colliding-pulse dye laser.1 Just over 20 years later, in 2003, a new barrier was broken when subfemtosecond pulses were achieved by a collaboration between Theodore Hänsch and Ferenc Krausz and their colleagues.2
To accomplish this feat, the output from a waveform-controlled chirped-pulse-amplification Ti:sapphire amplifier system was passed through a hollow-fiber/chirped-mirror compressor stage to reduce the pulse duration down to 5 fs, with energy of 300 μJ and peak powers of more than 1011 W. This in turn was sent into an evacuated beamline and focused into a neon-gas jet. The extraordinarily high field intensity induced gigantic atomic-dipole oscillations-containing high-frequency components that extended into the extreme-UV and soft-x-ray spectral regions-producing individual 650-attosecond pulses at a 13-nm wavelength (93-eV photon energy).
Although it is the intensity of the 5-fs pulse that leads to the x-ray emission, it is the waveform control that makes every pulse identical; subjecting each atom to the same electric-field perturbation causes it to follow the same path and produces the coherent x-ray emission.
This collaboration between the fields of precision frequency metrology and high-intensity ultrafast-laser physics marks the beginning of a new form of coherent control with single or few-cycle pulses, and opens the door to the world of “attophysics”-the study of physical process on the attosecond timescale.
Phase becomes important
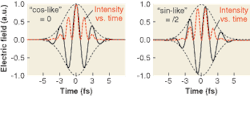
The wave packet in a 100-fs ultrafast laser-the carrier envelope-is ultrashort, but on a wavelength scale is still long enough for an electric-field oscillation of many cycles. As one moves to shorter and shorter pulses, however, the number of cycles decreases; at 5 fs, only two electric-field oscillations fit in the wave packet.
For nonlinear processes, including high-harmonic generation, attosecond-pulse generation, and photoelectron emission, the phase of this very short packet now becomes extremely important. The maximum electric field is much different for a cosine wave, with the peak of the electric field centered in the pulse, than for a sine wave, which has a double-peak of the electric field at a slightly lower field strength (see Fig. 1). In addition, because of the random nature of the phase, many effects are averaged out and are not possible to observe.
The difficulty is that, although the pulse travels through the oscillator cavity as a single packet, there is no coupling between the phase velocity (with which the field components propagate) and the group velocity (with which the envelope itself travels). In fact, because of dispersion in the cavity, these two velocities are not the same. As a result, there is a phase shift or “slip” from round-trip to round-trip between the maximum of the envelope and the underlying carrier field.
As pulses become shorter, and thus their associated bandwidth larger, the effect of dispersion grows. In any optical material, the index of refraction is a function of wavelength; the wavelengths at the short end of the envelope will travel at a different speed than pulses at the long end of the spectrum, stretching the pulse beyond its transform limit. To produce short pulses, it becomes necessary to correct for this dispersion coming mainly from the Ti:sapphire crystal itself, but also from the one meter or more of air.
Adding prisms to a cavity is one method for adding negative dispersion: the prism sequence creates different path lengths for the different wavelengths. Prisms have an inherent limitation, however, in that they can correct for second-order dispersion but cannot correct for higher orders at the same time. In fact, the material most commonly used, fused silica, corrects for second-order dispersion but contributes to unwanted third- and fourth-order dispersion. Also, theoretical and experimental work shows that as beam-pointing fluctuations occur, they transfer into phase noise because of the geometric dispersion of the prism sequence.3
Chirped dispersive mirrors
In 1994, researchers at the Technical University of Vienna and the University of Budapest introduced an alternative to prisms: the use of chirped dispersive mirrors. These dielectric-cavity mirrors are coated so that different wavelengths have different penetration depths (see Fig. 2). Dispersive mirrors remove the need for intracavity elements. They also make it possible to tailor the correction to include higher orders. In the first results, the construction of an oscillator was reported that had a bandwidth of more than 91 nm, compressible to a then record-short pulse of less than 11 fs. Chirped dispersive mirrors offer another advantage-that of decoupling of beam-pointing fluctuations from phase noise, due to the lack of elements with geometrical dispersion.
Although proper laser design can minimize or eliminate some sources of phase noise, it is possible to synchronize the group and phase velocities with the addition of active stabilization, called carrier-envelope-phase (CEP) stabilization. To do this, one must first be able to measure a value related to the phase slip, and then find some adjustment to the oscillator that effectively and uniquely alters the phase.
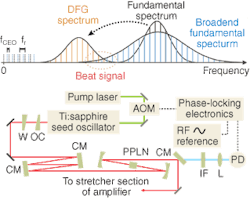
Interest in fixed-frequency combs has motivated work on this very problem. The scheme most commonly used to generate a feedback signal is a so-called “f-to-2f” interferometer. In this technique, part of the oscillator’s output is split off and focused into a photonic-crystal fiber to produce a spectrum spanning more than an octave; the red end is then frequency-doubled into the blue and combined with the blue part of the spectrum out of the fiber. This combination produces a beat signal that contains information about the change in phase and can be used as a feedback signal for control electronics.
The next task is to find a way to rapidly influence the phase. Some of the first work on frequency combs was with prism-based systems. By slightly adjusting the tilt of the mirror behind the prism sequence, and adjusting the cavity length via a folding mirror, it is possible to control the phase by continuous adjustment of the cavity length. This approach, however, is limited by the inertia of these mechanical parts.
Prismless oscillator
A faster and more elegant feedback approach was adopted for dispersion-mirror-based oscillators. The elimination of intracavity prisms greatly reduces coupling of beam pointing to CEP noise; in fact, in a direct comparison, the prismless oscillator shows an improvement of a more than ten times lower noise figure.
Feedback is accomplished by exploiting the group-phase contributions from the Kerr effect itself. Thin glass wedges are used to control the coarse dispersion of the oscillator by varying the glass thickness. Then an acousto-optic modulator is placed between the continuous-wave pump laser and the Ti:sapphire oscillator. Fine adjustment is done by modulating the pump power of the laser into the crystal. This modulation in turn results in a modulation of the intracavity peak power of the pulses, which results in a modulation of the nonlinear part of the refractive index in the Ti:sapphire crystal, fine-tuning the dispersion of the oscillator to control the phase slip.
In February of 2005, researchers at the Technical University of Vienna published a new technique for generating a beat signal.4 Theory predicts that the information about the carrier-envelope phase can not only be detected using frequency doubling and beating, but also from difference-frequency generation and beating. This allows for the setup of a monolithic implementation for the required feedback signal.
Monolithic approach
With the use of dispersive-mirror technology, it is possible to create a broadband oscillator producing more than 300 nm of bandwidth. This allows for difference-frequency generation (DFG) in a periodically poled lithium niobate crystal, which generates a signal in the 1.2- to 1.5‑μm range. At the same time, self-phase modulation also generates frequency components in the near-IR, which can beat with the DFG signal, providing the signal for the feedback. This new monolithic DFG scheme, now commercially available (the FemtoSource Rainbow DFG/FemtoPower CEP), is a stable and compact implementation with a major improvement in signal-to-noise levels.
In contrast to oscillators directly generating an octave-spanning spectrum, the DFG approach produces a higher spectral power density at the same output power. Also, the wider the spectrum an oscillator produces, the larger the losses from dielectric coatings at the edge of the supported bandwidth, which also affects the oscillator efficiency and output power. Thus, the DFG stabilization approach offers the bandwidth necessary for generating a strong beat signal and the high spectral power density appropriate for seeding an amplifier.
It is important to note that in amplifying CEP-stabilized pulses, beam-pointing-to-noise coupling should also be kept low in the stretcher and compressor. This is accomplished by introducing as little geometric dispersion as possible. In the FemtoPower amplifier design, for example, this is done by eliminating gratings and using an in-line glass stretcher along with a prism stage for the final compression.
The first application of ultrafast CEP stabilization to produce attosecond pulses may lead to the realization of the dream of an effective tabletop x-ray laser, in addition to providing a method of electronic spectroscopy to peer into the electronic processes that govern the creation and destruction of chemical bonds. Other applications are already unfolding.
REFERENCES
1. R. L. Fork, B. I. Greene, and C. V. Shank, Appl. Physics Lett.38, 671 (1981).
2. A. Baltuška et al, Nature421, 611 (February 2003).
3. F. Helbing, G. Steinmeyer, and U. Keller, IEEE J. Quantum Electronics 9(4) (July/August 2003).
4. T. Fuji et al, Ultrafast Lasers Letters30(3)
(February 2005).
5. U.S. Patent 5,734,403.
6. Rauschenberger et al., ICUIL 2004.
ANDREAS ISEMANN is worldwide sales manager and ANDREAS ASSION is product manager at Femtolasers Produktions, Fernkorngasse 10, A-1100, Vienna, Austria; e-mail: [email protected]. MARY ESSARY is general manager of FemtoLasers, 239 Stow Rd., Harvard, MA 01451.