The wave nature of light can cause it to diffract, effectively bending around corners. Ordinary experience, however, leads us to believe that in most cases light travels in straight lines, called rays. This rectilinear interpretation of light dates from at least the time of Euclid in the third century BC, and it still forms the chief premise of geometrical optics today. In fact, one of the most powerful tools available for modern optical design involves a computer-aided technique called ray tracing. An optical system is evaluated using ray tracing by tracking straight paths of light through each element.
Light rays can be constructed from Huygens wavelets by drawing arrows perpendicular to the wavefront. For an ideal plane wave, in which all the points of constant phase on all the wavelets define parallel planes in space, all the rays are parallel to each other and point in the direction of propagation. Studying the behavior of a single ray (or a bundle of rays) when it interacts with optical elements describes the essence of geometrical optics (see photo).
Choosing the right path
Perhaps the most familiar law of Euclidian geometry states that a straight line forms the shortest path between two points. About four centuries after Euclid, an optical version of this principle was written down by Hero of Alexandria, who used it to deduce the law of reflection.
Hero maintained that light takes the shortest possible path between two points. For a reflected ray of light, the shortest path can be found by following the central ray of the figure as it makes its way from point A to point B via line M, representing a mirror.
The figure depicts two possible paths for a Huygens wavelet emanating from point A and reflected to point B: ACB and ADB. To determine which path is shorter, we drop a perpendicular from B through E on the mirror and terminate it at B'. Point B' is chosen such that EB = EB'. This construction forms two isosceles triangles (BCB' and BDB') in which CB = CB' and DB = DB'. Therefore, the path length ACB equals ACB'. The same argument holds for ADB and ADB'.
The shorter path suddenly becomes obvious. It is the straight line ADB', which is just ADB. In fact, because it is a straight line, ADB' represents the shortest possible path of any reflected ray from A to B.
An interesting consequence of the geometric construction in this figure concerns the included angles BDE and ADC. Since EB = EB', we know that the line M bisects the angle BDB'; therefore, the angle EDB' equals the angle EDB'. That means angles EDB' and ADC are also equal, because ADB' and CDE form two intersecting straight lines. Consequently, angles BDE and ADC are equal as well.
The equality of these last two angles expresses the law of reflection, which states that the angle of reflection equals the angle of incidence—a relationship usually written as
θr = θi
These two angles equal each other only when the incident and reflected rays trace the shortest possible path. (Angles of incidence are usually measured from the surface normal, however this does not invalidate the above derivation.)
In optics, however, the shortest possible path isn't always the path taken. For example, consider a light ray that encounters a block of transparent glass. The shortest path between points A and B should be the straight line AB. But instead of taking the shortest path, the light ray follows the quickest route from A to B, which is ACB. In this case, the quickest route is not the shortest one. Why? Because the speed of light is different in each medium.
Most of us regularly apply the same principle of least time when driving from one place to another. The quickest way to our destination is often to spend more time on a highway where the speed limit is 55 mph and less time on surface streets where the speed limit is 35 mph, rather than travel a more direct route over slower roads. If we carefully balance our highway miles vs. surface-street miles, we can minimize the transit time compared to any other path we might choose.
The transit time for the light ray would equal the total time spent in each medium, or t = AC/v1 + CB/v2, where AC and CB define the path lengths in air and glass, respectively, and v1 and v2 represent the velocities of light along each path. The transit time reaches a minimum when the ratio of the two velocities equals the ratio of the sines of the incident and transmitted angles. That is:
v1/v2 = sin θi/sin θt
Now, the ratio of the speed of light in a vacuum to its speed in air (c/n1) can be expressed as a single factor, n1, which can be thought of as an "impedance" factor. For example, if our car has a top speed of 100 mph but the speed limit on the highway is 55 mph, then the impedance factor would be 100/55 or 1.8. On surface streets, the factor is even higher, at 100/25 or n = 2.9. For a light ray in glass, the factor is about 1.5 (n2 = 1.5); therefore the speed of light drops 1.5 times, or n2 = c/n2. With this in mind, we can rewrite Eq. 2 in terms of n1 and n2:
n1sin θi = n2sin θt
This important expression is called Snell's law of refraction, after Willebrord Snell van Royen (1591-1626), who determined it empirically. Ray-tracing programs rely heavily on this law to analyze the performance of optical components and systems. The factor n, call the index of refraction, characterizes a critical property of optical media. So many qualities of an optical system depend on the value of n, which can vary significantly from one material to another, or even within a single substance. The refractive index is a function of wavelength and, depending on the material, can also be dependent on temperature and other environmental variables.
Reflection, refraction, Fermat
It was the French mathematician Pierre de Fermat (1601-1665) who derived the law of refraction using the principle of least time, an approach that has come to be known as Fermat's principle. In its most general form, Fermat's principle represents the fundamental physical tenet underlying all of geometrical optics. In addition to the law of refraction, a variety of other important optical laws follow logically from this far-reaching doctrine. For instance, Hero's principle and the law of reflection express a special case of Fermat's principle in which the index of refraction of the medium does not change.
Another consequence of Fermat's principle concerns the principle of reversibility or reciprocity. This principle states that if the direction of propagation were reversed, the light ray would retrace its path through the optical system. Fermat's principle makes this assertion patently obvious in Figure 2, because if ACB truly traces the quickest route from A to B, then the reverse direction (BCA) must be the fastest as well. Also, notice that in the figure the original ray (ACB) bends towards the normal as it enters a medium with a higher index of refraction, whereas in the opposite direction the ray bends away from the normal as it passes into a medium of lower index.
The most compelling application of Fermat's principle concerns the situation in which the quickest route between two points in an optical system consists of not just one path but an infinite family of paths. Such is the case in imaging systems that use one or more optical elements to gather light rays from one point and to focus (image) them at another point. Determining the shape, content, and position of these optics is the single most important function of geometrical optics.
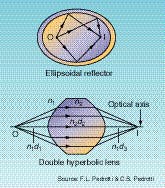
Special reflecting and refracting shapes can be made to focus all or part of the light rays radiating from a particular point; two good examples are the ellipsoidal reflector and the double hyperbolic lens (see Fig. 1). Inside the ellipsoidal reflector, all the reflected light paths from point O to point I are the same distance and therefore must also be the quickest routes. So Fermat's principle holds for all these reflected rays. This follows from the geometrical definition of an ellipsoid, which is the set of all the points whose combined distance from the two foci is a constant. This type of reflector, incidentally, makes an excellent light collector for optically pumped lasers.For the hyperbolic lens, the transit times of rays passing from point O to point I are made equal by the shape of the intervening glass medium. In other words, the optical path lengths of the rays are all the same. Optical path length is defined as nd: the product of the index of refraction (n) and the physical distances in the medium (d). So even though the central ray passing through the lens has the shortest physical path, it also has the most glass to transverse, making the optical path length equal to the others.
These two examples belong to a family of perfect imaging shapes called Cartesian surfaces. Because spherical surfaces are easier to fabricate, however, they have more practical significance. Spherical surfaces do not bring all rays to a perfect focus, so their refractive and reflective imaging properties must be approximated. The approximation is made by looking only at rays that lie close to the optical axis (for example, the central ray in Fig. 1). Geometrical analysis of these so-called paraxial rays defines the field of Gaussian optics.
Gaussian optics
In the Gaussian approximation, even spherical surfaces become perfect imagers. Take, for example, a thin lens with two convex spherical surfaces. Light rays that radiate from specific points on the object will converge to corresponding points on the image plane of the lens. Optical attributes such as the image-plane position or image size (magnification) depend on the position of the object relative to the primary focal point, which itself depends on the curvature of the two spherical surfaces and the two indices of refraction. A set of simple formulas that characterize the Gaussian optical properties of various spherical surfaces under different circumstances can be geometrically derived.
In certain situations, the optical surface may form a virtual image in which the light rays do not converge on any image point (or plane), but instead seem to diverge from a point behind the optical surface. Convex mirrors and concave lenses have this property. Unlike real images, virtual images cannot be projected onto a screen.
The same geometrical constructions used to describe the optical traits of a single thin lens also can be applied to a combination of two or more thin lenses. In such an arrangement, the image of the first lens becomes the object of the next, and so on. But things get a little more complicated as lens thickness increases. Here, the Gaussian formulations must account for longer path lengths through each lens.
Less than perfect
The Gaussian approximation offers a simple and convenient explanation of spherical optics, but real-world applications expose the limitation of this approach. Notably, there are five effects that render optical surfaces less than perfect: spherical aberration, coma, astigmatism, field curvature, and distortion. These are called Seidel aberrations after the German mathematician Ludwig Philipp von Seidel (1821-1896).
Spherical aberration in a lens results from the fact that the outer regions refract light rays more than the central regions do. Consequently, the focal length of the outer perimeter is shorter than that of the inner region, leading to a foggy halo of unfocused light surrounding the paraxial focal point.
Coma is caused by light rays that illuminate an optic at an angle to its optical axis. This off-axis aberration smears point images into comet-like blurs, hence the name.
Astigmatism is another off-axis effect, which generates perpendicular focal lines (not points) that lie in two different focal surfaces. The degree of separation between these curved focal surfaces determines the severity of astigmatism.
Field curvature is related to astigmatism. If the two focal surfaces of an astigmatic system can be made to coincide, but the curve remains, then the effect is field curvature. A camera whose lens suffers from curvature will take pictures that blur towards the edges because the focal surface (called the Petzval surface) is not flat like the film.
Distortion, the last of the Seidel aberrations, results from an uneven lateral magnification across the field of view. Distortion comes in two basic varieties: barrel or pincushion. If lateral magnification increases towards the outer regions of the field, then pincushion distortion appears. Conversely, an inverse variation of magnification across the field leads to barrel distortion.
The five Seidel aberrations can occur even when the light is monochromatic. When light consists of more than one color, a sixth effect can occur.
Chromatic aberration arises in lenses because the index of refraction is a function of wavelength. In the visible spectrum, refraction decreases with increasing wavelength: therefore, red images focus farther away from a lens than do blue images. White light sent through prisms and the phenomenon of rainbows, both illustrate dispersion of the visible wavelengths. Mirrors, on the other hand, do not refract light and do not suffer from chromatic aberration. As lovely as rainbows are, chromatic dispersion is only occasionally desirable in optical systems. A variety of clever techniques have evolved to correct for these aberrations.
Even with the most sophisticated ray-tracing programs, though, the ultimate challenge for optical designers originates with the wave nature of light, because the diffractive effects of light waves place fundamental limits on the resolution of optical systems. Nevertheless, the advent of near-field optics, which has led to a number of practical sub-wavelength microscopy methods, has made it possible to dodge even this seemingly inescapable obstacle. In the end, the only limitation to optical design may be our imaginations.
About the Author
Thomas V. Higgins
Contributing Editor
Thomas V. Higgins was a contributing editor for Laser Focus World, covering science and technology.