Quantum information Processing: Photons promise an exciting route to quantum computing
JEREMY L. O’BRIEN
Quantum information science seeks to answer the question, “What additional power and functionality can be gained by harnessing uniquely quantum-mechanical effects in the encoding, transmission, and processing of information?” Anticipated future technologies in this area include quantum communication, which promises the ultimate security based on the laws of physics; quantum metrology, which promises the highest measurement precision allowed by nature; and quantum lithography, which aims to use entangled states of light to define features smaller than the wavelength of light. Perhaps the most profound future technology is a quantum computer that promises exponentially faster operation for particular tasks. Of the various physical systems being pursued, an all-optical quantum computer, which encodes quantum information in single photons, has emerged as a leading approach.1, 2
Single photons as quantum bits
Single photons make excellent quantum bits, or qubits (two-level quantum-mechanical systems), because they are very well isolated from their environment: a photon propagating in free space experiences a vacuum to good approximation. This is in contrast to almost all other physical systems exhibiting quantum-mechanical phenomena, which are typically very small and very cold: they are subject to numerous disturbances from their environment. For example, an electron’s spin can be used to encode a qubit, but it would be subject to noise due to interactions with anything that is charged or has a spin in its environment. A single photon, on the other hand, if prepared in a horizontal polarization state and reflected off a mirror on the Moon, would still be horizontally polarized when it returned. Of course this neglects the problem of how to store photons in the computer!
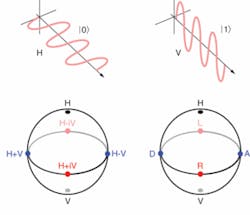
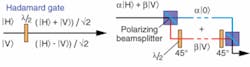
In addition to low noise, single photons allow one-qubit quantum logic gates (the quantum analogue of one-bit gates like the NOT gate, which takes a zero to a one and a one to a zero) to be implemented essentially for free. This is because encoding in polarization allows all of the conventional polarization rotations available with birefringent waveplates (see Fig. 1).
For these reasons, single photons were one of the earliest systems considered for quantum information, and have found wide application in quantum communication.3, 4 Here the polarization degree of freedom of single photons is most appropriate for free-space communication, while a “time-bin” encoding is more suitable in optical fibers, which tend to scramble polarization. Spatial encoding, where a qubit is encoded by a single photon in one of two optical modes, is particularly useful for quantum computing.Massive optical nonlinearity?
Unfortunately the photon’s low-noise virtue is also a curse: to process quantum information, we must make photons “talk” to each other to allow the interactions required for two-qubit gates. These two-qubit gates must be able to “entangle” the state of the two photons—the canonical example is the controlled-NOT gate (CNOT). This is the quantum analogue of the XOR gate (see en.wikipedia.org/wiki/XOR_gate), which flips the state of the target qubit only if the control qubit is in the “1” state. In contrast to the XOR, the CNOT can have input and output states that are a quantum mechanical superposition.
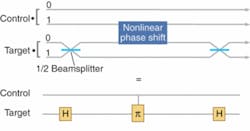
Realizing a two-photon CNOT gate is difficult (see Fig. 3). The spatially encoded target qubit is sent into a conventional Mach-Zender interferometer such that the photon goes into a superposition inside the interferometer, but always exits in the same logical state that it entered; if it enters in the 1(0) mode, it exits in the 1(0) mode, and similarly for any superposition. To realize a CNOT gate, we need the presence of a single photon in the control “1” mode to induce a π phase shift in the target interferometer. One could imagine doing this with a nonlinear optical material, such as a cross-Kerr medium. However, it quickly becomes apparent that the strength of such a nonlinearity would need to be massive—far beyond the most advanced materials we have yet to conceive.The requirement for a massive optical nonlinearity was a seemingly impassable roadblock to optical quantum computing until 2001, when Knill, Laflamme, and Milburn (KLM) proposed a radical solution based on inducing such a nonlinearity via single-photon detection (see www.laserfocusworld.com/articles/298397).5 This theory introduces two additional photons to act much like a catalyst in the CNOT gate. For example, a two-photon CNOT gate could be realized by introducing two extra photons and mixing all four photons in a linear optical network, essentially a network of beamsplitters that forms several nested interferometers. Detection of two of the four photons (not necessarily the two extra ones) at particular outputs of the network, combined with nondetection at other outputs, would signal success of the CNOT gate. Unfortunately the probability of success was not 1, but when successful, the gate would implement the CNOT operation.
The problem of having probabilistic gates was overcome by introducing more photons to boost the success probability and using a trick called quantum teleportation, which was demonstrated in 1997. The complete scheme represented a radical departure from the conventional wisdom of the day, which held that a massive optical nonlinearity would be required to realize a quantum computer operating on single photons.
Although this impressive breakthrough showed that all-optical quantum computing was in principle possible, the task of manipulating many photons was daunting. Nevertheless, several groups set out to demonstrate the fundamental building block—an all-optical CNOT gate.
A two-photon CNOT gate
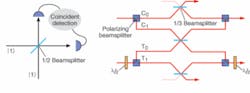
A two-photon CNOT gate based on a measurement-induced optical nonlinearity was experimentally demonstrated in 2003 (see Fig. 4).6 In this scheme, there are only two photons, and detection of these photons is the success signal.At the heart of the operation of this gate is quantum interference with two photons: when two identical photons arrive simultaneously at the inputs to a 50% reflective beamsplitter, the probability of detecting a photon at each of the outputs is zero; in stark contrast to our classical intuition, which suggests that this probability should be 1/2. The reason is that in quantum mechanics we must sum indistinguishable probability amplitudes (in this case, the amplitude for both photons being transmitted, t.t, and the amplitude for both photons being reflected, r.r) and square the result to get a probability. Since probability amplitudes are complex numbers, they can cancel one another (in this case, r.r = t.t because of the phase shift imparted on reflection). When the beamsplitter reflectivity is not 50%, the probability is not zero, but is below the classically expected value.
In the two-photon CNOT gate, the control and target photons are converted between polarization and path encoding and back again. This means that the 50% beamsplitters shown in Fig. 3 that implement Hardamard or “H” gates can now be realized by a half-wave plate oriented at 22.5°, when the photons are polarization encoded. The controlled-π phase shift is then realized by the linear optical network consisting of three 1/3 beamsplitters, where quantum interference induces the required phase shift. With a probability of 1/9, the two photons exit this circuit in the control and target modes—in these cases the CNOT logic has been applied to their polarization state. Although this circuit implements the required CNOT logic, it destroys the photons in the process. Gates that use additional photons have overcome this problem.
Where to now?
Improvements to the original KLM scheme, along with several experimental demonstrations of fundamental quantum logic gates gave cause for optimism. However, a worryingly large resource overhead remained, arising from the additional photons required to make the probabilistic gates near-deterministic: greater than 10,000 pairs of entangled photons would be required to realize a single CNOT with success probability greater than 95%. Fortunately new theoretical schemes have been developed that reduce this overhead by orders of magnitude.
Today the major challenges facing all-optical quantum computing are the realization of high-efficiency single-photon sources and detectors, and their integration into scalable optical circuits, such as the silica-on-silicon waveguide circuits currently being developed at Bristol (previous proof-of-principle demonstrations have relied on bulk optical elements and photons propagating in air). Finally, a number of hybrid approaches have been proposed, and are actively being pursued, in which a different type of optical nonlinearity is introduced.
ACKNOWLEDGMENTS
The author thanks the U.K. Engineering and Physical Sciences Research Council, the U.K. Quantum Information Processing Interdisciplinary Collaboration, the U.S. Disruptive Technologies Office, the EU Integrated Project Qubit Applications, the Leverhulme Trust, and the Daiwa Anglo-Japanese Foundation.
REFERENCESREFERENCES
1. http://qist.lanl.gov/qcomp_map.shtml
2. J.L. O’Brien, Science 3(18) 1567 (2007).
3. G.J. Milburn, Phys. Rev. Lett. 62, 2124 (1989).
4. N. Gisin, et al., Rev. Mod. Phys. 74, 145 (2002).
5. E. Knill, et al., Nature 409, 46 (2001).
6. J.L. O’Brien, et al., Nature 426, 264 (2003).
JEREMY L. O’BRIEN is a reader in research at the Centre for Quantum Photonics, H.H. Wills Physics Laboratory and Department of Electrical and Electronic Engineering, University of Bristol, Merchant Ventures Building, Woodland Road, Bristol, BS8 1UB, England; e-mail: [email protected]; www.phy.bris.ac.uk/people/jeremy_obrien/cqp.html.