PHOTONIC FRONTIERS: NEGATIVE-INDEX-MATERIALS: Negative-indexmaterials are on positive track
Materials with negative refractive indexes have become one of the decade’s surprise hits in photonics. First demonstrated at radio frequencies, such metamaterials have recently produced negative refraction at visible wavelengths. Early experiments used only subwavelength structures with a single metamaterial layer, but recently the first “three-dimensional” negative-index optical materials have been demonstrated, and more new developments are emerging at a rapid pace.
Ironically, the potential application of metamaterials most publicized in the popular press—invisibility cloaks of the sort used by Harry Potter—doesn’t actually require negative-index materials. But negative refraction promises many more innovations that would offer dramatic new optical capabilities, such as “superlenses” for subwavelength imaging. It is still early days as researchers explore the newly discovered territory, but it is clear things are going to get even more interesting.
Basics
In optics refractive index n is a fundamental property of a material, but in electromagnetic theory n actually is the square root of the product of two more fundamental quantities, the electrical permittivity ε and the magnetic permeability µ: n = ±√εµ.
Permittivity is related to the dielectric constant (also denoted ε but defined for a static field). By convention both permittivity and permeability normally are given relative to the corresponding qualities of a vacuum, which are defined as equal to 1.
Both permittivity and permeability are positive for conventional transparent optical materials such as glass and water, so their refractive index is positive. Other materials, such as gold and silver, have negative permittivity and positive permeability at visible wavelengths, so their refractive index is imaginary and they are opaque. Materials that have positive permittivity and negative permeability negative are also opaque. But in 1968, Russian physicist Victor Veselago suggested that materials would have a negative refractive index if they had negative values of both permittivity and permeability.
That seemed an academic matter at the time, because no natural materials had such properties at optical wavelengths. But in the late 1990s, John Pendry of Imperial College London (London, England) developed artificial metamaterials composed of conductive components designed to make both permittivity and permeability negative at wavelengths large enough that they don’t “see” the components as such, but only as a uniform material. The effect occurs above a resonant frequency, and the magnitude of the refractive index depends on frequency. After initial demonstrations at radio frequencies, components were shrunk to smaller sizes for use at higher microwave and eventually optical frequencies.
Properties of negative-index materials
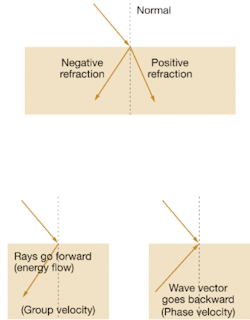
As Snell’s law predicts, negative-index materials bend light backward, but negative refraction produces strange effects (see Fig. 1). Energy flows from the positive-index material at the top to the negative-index material at the bottom, moving at the material’s group velocity (left). Yet waves in the negative-index material travel in the opposite direction, moving toward the top at the phase velocity (right).
Negative refraction changes the rules of optics. In 2000, Pendry observed that a negative-index lens would focus not just the normal propagating waves, but also evanescent waves, allowing the possibility of making a “superlens” with subwavelength resolution.1 The superlens requires only a flat slab of negative-index material. If the material has both ε = -1 and µ = -1, corresponding to n = -1, the slab acts as “negative space,” wrote David Smith of Duke University (Raleigh, NC), Pendry, and M. C. K. Wiltshire of Imperial College. “Optically speaking, it is as if the slab had grabbed an equal thickness of empty space next to it and annihilated it. In effect, the new lens translates an optical object a distance 2d (twice its thickness) down the axis to form an image.”2
The refractive index of a metamaterial can vary strongly with frequency, especially near resonances. This limits the range of wavelengths at which negative refraction occurs, but it also promises new types of nonlinear devices. For example, the index can change sign within the bandwidth of a short-pulse laser source, so coupling into and out of the metamaterial would differ between two parts of the spectrum. The index also can vary in space, and the change in refraction between regions of positive and negative index can generate new nonlinear phenomena, including “backward” phase matching, Vladimir Shalaev of Purdue University (West Lafayette, IN) wrote in a review article.3
Negative-index materials have some inherent limitations, including high loss compared to conventional transparent materials. But theorists are considering ways that gain could be added to offset the losses. Alexander K. Popov of the University of Wisconsin (Stevens Point, WI) and Shalaev have suggested using optical parametric amplification.4
Optical demonstrations
Negative-index materials reached the near-infrared in a series of demonstrations beginning in 2005 that spanned wavelengths of 1.4 to 2 µm. The approaches differed in detail, but shared important features. Unit cells of conductive metal film were deposited on top and bottom of a thin dielectric layer, producing a negative-index layer much thinner than the wavelength of light transmitted. For example, Shalaev’s group designed unit cells consisting of pairs of gold nanorods 780 × 220 nm that were offset from one another on top and bottom of a silica layer, producing a subwavelength structure with refractive index of roughly -0.3 at 1.5 µm.5
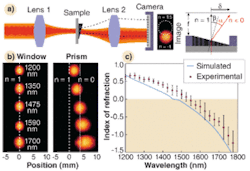
The first demonstration of negative refractive index at visible wavelengths was by Gunnar Dolling, then at the University of Karlsruhe (Karlsruhe, Germany) and colleagues. They fabricated a microstructure with a thin layer of magnesium fluoride sandwiched between two thin silver layers. Then they etched the 97-nm-thick structure to produce a grid or fishnet structure with wires and holes in the grid similar in size. This single functional layer had negative index between 760 and 800 nm, with the peak negative value of -0.6 at 780 nm.6 The group later made stacks of as many as three functional layers, limited by fabrication difficulties and transmission losses, but even those structures were much thinner than a wavelength.Like the Karlsruhe group, Valentine used a fishnet structure, but his fishnet contained eleven 30 nm layers of silver alternating with ten 50 nm layers of magnesium fluoride (MgF2), equivalent to ten layers of unit cells a total of 830 nm thick (see Fig 2, left and center). Fabricating the structure as a prism with a small slope allowed Valentine to bend light backward. The refractive index decreased as wavelength increased. At 1200 nm the index was 0.63, dropping below zero near 1500 nm and reaching -1.23 at 1775 nm where measurements stopped; the observed refraction changed with wavelength (see Fig. 3).7
Although the Berkeley “bulk” sample was less than a wavelength thick, with 10 unit cells stacked together it had properties notably different from single unit-cell thickness. “A single layer of metamaterial is resonant,” Valentine says, but bulk material is not, so its refractive index is negative across a wider spectral range. Strong coupling between the layers reduces light absorption, so the thicker structure transmits more light. The effect is also evident in the figure of merit, a measure of transparency defined as the ratio of ratio of real to imaginary refractive index; the larger the value, the more light is transmitted.
Another Berkeley student, Jie Yao, also observed negative refraction in a different type of bulk metamaterial, arrays of 60 nm silver nanowires embedded in alumina.8 However, the effect—observed at 660 and 780 nm in layers up to 12 µm thick—occurred only for transverse-magnetic (TM) polarized light incident on the ends of the nanowires. Yao attributes the effect not to a negative phase velocity, but to the dispersion and inherent anisotropy of the structure.
Outlook
Research on negative-index materials is in the early stages, and much remains to be learned about device fabrication, structure, performance and applications. Developers need to scale up sizes and improve transmission, as well as to study how the performance of actual devices affects the prospects for practical superlenses. They also need to work out what structures would work best for particular applications. Anisotropy may be good for some applications, but others may require isotropic materials.
The challenges are real, but the excitement is clear. Fabricating negative-index materials is opening new optical possibilities that we’re only beginning to explore. Expect the unexpected, like John Pendry’s recent theoretical paper showing an intimate link between negative refraction and time reversal, and proposing a new type of lens based on a two-dimensional hologram written in a thin sheet of highly nonlinear material.9
REFERENCES
- J. Pendry, Physi. Rev. Lett. 85, 3966 (2000).
- D.R. Smith, J. Pendry, and M.C.K. Wiltshire, Science 305, 788 (Aug. 6, 2004).
- V. Shalaev, Nature Photonics 1, 41 (Jan 2007).
- A.K. Popov and V.M. Shalaev, Opt. Lett. 31, 2169 (2006).
- V. Shalaev et al., Optics Lett. 30, 3356 (Dec. 15, 2005).
- G. Dolling et al., Optics Lett. 32, 53 (Jan 1, 2007).
- J. Valentine et al., Nature 455, 376 (Sept. 18, 2008).
- J. Yao et al., Science 321, 930 (Aug. 15, 2008).
- J. Pendry, www.sciencexpress.org (Aug. 28, 2008) doi10.1126/science.1162087.
About the Author
Jeff Hecht
Contributing Editor
Jeff Hecht is a regular contributing editor to Laser Focus World and has been covering the laser industry for 35 years. A prolific book author, Jeff's published works include “Understanding Fiber Optics,” “Understanding Lasers,” “The Laser Guidebook,” and “Beam Weapons: The Next Arms Race.” He also has written books on the histories of lasers and fiber optics, including “City of Light: The Story of Fiber Optics,” and “Beam: The Race to Make the Laser.” Find out more at jeffhecht.com.