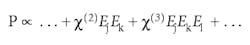The power in crystals
The principal of superposition states that different wavelengths of light do not interact when they occupy the same space. This situation is altered in a dramatic way in nonlinear optics (NLO), which describes the reaction of a material to intense light. Under the right conditions, a material can act as a sort of catalyst, remaining unchanged itself but converting laser beams into a virtual rainbow of new wavelengths.
The material truth
Nonlinear optical effects can take place in all phases of matter. Inorganic crystals have proven historically to be the most convenient and effective media. However materials currently under development may soon alter this situation.
The nonlinear polarization in a material, which is responsible for the generation of new wavelengths, can be expanded as a power series of the electric field of the incident light:
null
Each of the terms is modified by the susceptibility, χ, a tensor quantity.
A tensor is the most general product of two or more vectors. The number of vectors multiplied equals the rank of the tensor. The susceptibility tensor for second-order effects χ(2) = χijk relates each of the three components of the polarization—Px, Py, and Pz to the nine products of the two applied light fields, for a total of 27 terms.
For convenience, the second-order susceptibility is converted into nonlinear optical coefficients dijk. Different definitions and dimensions are used, so absolute values of dijk should be used with care. The most common second-order effect, and the most important NLO phenomenon, is second-harmonic generation (SHG).
Similar considerations hold for the third-order susceptibility, a fourth-rank tensor. Third-order coefficients are responsible for third-harmonic generation, parametric conversion, and stimulated scattering, among many other effects. There are 81 possible third-order terms.
Crystal symmetry
Crystals are grouped into seven symmetry classes, characterized by three vectors that define the crystal sides, plus the angles between them. Cubic crystals are the most symmetric; the least symmetric, triclinic, has three different sides set at three different angles (see Fig. 1). In addition, crystals fit in one of 32 so-called point groups, each of which belongs to one of the symmetry classes.
null
A careful examination of the symmetries in a material is indispensable to understanding its nonlinear optical properties. For instance, 11 of the point groups are "centrosymmetric," meaning that the structure of the crystal remains unchanged along a direction reversed 180∞. No second-order effects can take place in centrosymmetric crystals.
Other symmetry considerations further simplify the second-order coefficients, reducing the second-order tensor to 18 terms. Additional details for individual crystals usually reduce this to between one to three significant terms. Similar simplifications occur for higher-order NLO.
Practical considerations
Besides possessing a large nonlinear coefficient, a material should be transparent over a wide range, accept polishing and coating, and not be hygroscopic. It must be possible to grow the crystal in a reasonable period of time and in practical sizes.
The acceptance angle of the crystal affects parameters as varied as the length of the interaction of the NLO conversion and the minimum beam quality of the fundamental laser. The crystal must be resistant to optical damage. The incident beams thermally stress the material, and a failure of the crystal to support high fluences will limit its use for high average power.
Perhaps the most important constraint is that the crystal supports some form of "phase-matching." More will be said about this topic in next month's "Back to Basics" article but for now let it suffice that phase-matching is required for the incident beam(s) to transfer power to the newly generated beam. There are various phase-matching techniques, all of which rely on wavelength-dependent properties of the material.
Classic crystals
Nature is generous in supplying laser sources in the infrared, but stingy at shorter wavelengths. Interest in NLO materials, therefore, centers on the production of visible and ultraviolet light. Potassium dihydrogen phosphate (KDP) was among the first crystals used to produce useful levels of visible second-harmonic light.
Relative measurements of dijk can be obtained with better accuracy than absolute values, and values for different materials are often compared to KDP. It is easy to grow in solutions that produce high-quality crystals (see photo, below), with a transmission band from 200 to 1500 nm, and has a high optical damage threshold.
null
Potassium dihydrogen phosphate has a relatively small nonlinear coefficient. An important method for developing new crystals is to find a material with desirable qualities and to improve its shortcomings by creating isomorphs. Isomorphs substitute a new atom or molecule as a component while retaining the structure of the crystal. An early example is the substitution of deuterium for hydrogen in KDP to produce KD*P to increase NLO efficiency.
Another KDP isomorph, KTP (KTiOPO4) has still higher efficiency, and is a commonly used material for lower-power intracavity-doubled neodymium lasers. Green laser pointers are often made using KTP. Also, it is an important crystal for optical parametric devices with tunable outputs from red to the mid-infrared.
A piggyback on telecom
The widespread use of lithium niobate (LiNbO3) in optical networking gives this material great commercial importance. Its large electro-optic and acousto-optic coefficients make it the most commonly used material for waveguide substrates, as well as for Pockels cells, Q-switches, and so on.
Lithium niobate has a band edge near 400 nm, so it cannot be used to double wavelengths much shorter than 1 µm. It has a low damage threshold, characterized by "gray-tracking," in which lines appear in the crystal along the beam path. This damage has been known to heal itself, but it is an undesirable feature. Doping lithium niobate with magnesium raises the damage threshold.
Barium sodium niobate (BaNaNb5O15), also known as BaNaNNA, is similar to lithium niobate but is less susceptible to optical damage and has a nonlinear coefficient about three times larger. However, some BaNaNNA samples have shown poor optical quality. This material has been used for efficient second-harmonic generation of 1.06-µm light, and for parametric conversion.
Poling for more
The efficiency of doubling CW lasers can be problematic. To boost efficiency, certain types of crystals can be fabricated for "quasi-phase-matching". The fabrication method is called periodic poling.
Periodically poled lithium niobate (PPLN) is produced using its ferroelectric properties to reverse its principal axes in adjacent regions of the crystal. In the simplest case, the regions have a thickness equal to the coherence length for the NLO interaction. This allows the highest SHG coefficient to be used, which isn't the case in other phase-matching schemes.
The damage threshold has proven to be a limitation for the use of PPLN, exacerbated by the small crystal sizes required by poling. In addition, other NLO effects require added power in the fundamental wave. These considerations led to the development of periodic poling for other ferroelectric crystals, notably KTP and lithium tantalate. The recent development of PPRTA (rubidium titanyl arsenate) has also attracted interest.
BBO, LBO
The introduction of beta barium borate (BBO) and lithium triborate (LBO) in the late 1980s provided a combination of nonlinear efficiency and high damage threshold that significantly accelerated NLO development. Both materials are transparent well into the ultraviolet. Lithium triborate has the highest damage threshold of all commonly used NLO crystals, making it the material of choice for high-average-power applications.
Both materials are used to produce wavelengths shorter than 300 nm, but LBO has a lower birefringence that limits its UV phase-matching to certain combinations of longer wavelengths. It is often "temperature tuned" for phase-matching; that is, heating the crystal to a temperature at which its refractive index is the same for the fundamental and harmonic light. Compared to BBO, it has a significantly wider acceptance angle.
The birefringence of BBO gives it excellent phase-match capabilities, enabling it to produce tunable radiation from the near infrared into the UV. It is commonly used in parametric conversion, and for the generation of higher harmonics of neodymium lasers. Both crystals are slightly hygroscopic, and are relatively soft.
Adding cesium to LBO produces CLBO, a soft and hygroscopic material that nevertheless has grown in popularity for producing shorter wavelengths. The combination of CLBO properties allows a severalfold improvement in NLO efficiency.
Other materials, new horizons
The distinguishing characteristic of proustite (Ag3AsS3) is its infrared transmission, which extends beyond 13 µm, making it attractive for carbon dioxide laser wavelengths. Its nonlinear coefficient is about 300 times larger than that of KDP. The material is difficult to coat and to polish, however. There are a host of other crystals used in the infrared, including the related material silver gallium selenide (AgGaSe3). Crystals also exist that are specialized to a single application, such as optical phase conjugation.
A practical new crystal to generate wavelengths below 200 nm would have instant commercial success, but is an difficult challenge that so far has produced limited success. Cesium lithium borate (CLBO), for example, is transparent at wavelengths down to 180 nm, but it does not have enough birefringence to phase-match for wavelengths below 200 nm.
Organic NLO materials have nonlinear coefficients that for some processes are orders of magnitude greater than dielectric crystals, allowing NLO production using smaller, lower power, and less expensive lasers, but their optical quality is a drawback. However, practical nonlinear optical devices have been fabricated in laboratories using waveguides and microscopic structures made from organic compounds (see Fig. 2).
null
Organic NLO materials have the great advantage of being easy to make compared to inorganic crystals. Polydiacetylenes have attracted much attention because of their large third-order nonlinear coefficients, and an organic crystal known as DAST has also received high interest. Other organic materials that have been studied include phthalocyanines, ladder polymers, and polyacetylene.
A clever idea that has proven hard to implement is the addition of the laser gain material directly to a doubling crystal, thus producing a self-frequency-converted laser. This concept has been successfully demonstrated in the laboratory, mostly using rare-earth materials like neodymium in various forms of lithium niobate. Creating a stable, practical device, however, has proven difficult, in part because of phase-matching requirements.
Optoelectronics is still in its early stages, and as applications become more widespread, nonlinear materials will grow in importance to increase the range of laser technology.
Next month's article will review the techniques of second-harmonic generation.