Twice as good
The first nonlinear optical effect to be observed after the invention of the laser was frequency doubling, also called second-harmonic generation (SHG). Its potential was recognized immediately, but it took three decades for SHG to achieve its commercial promise. In part, this delay was the result of the need for improved laser sources, but much had to be learned about the SHG process itself.
Second-order nonlinear optical effects result from the second-order term in the polarization susceptibility of a material. This term describes the production of a new wave Ei(ωi) from the combination of two incident waves, Ei(ωi)Ek(ωk). Second-order effects include parametric oscillation and the Pockels effect, in which the frequency of one of the incident beams is taken to be zero (an applied DC voltage). The most remarkable second-order effect is second-harmonic generation.
Double or nothing
Second-harmonic generation is mathematically equivalent to two incident beams of the same frequency—that is, a single intense incident beam. A beam at frequency w is converted into one at frequency 2ω. Energy flows from the fundamental beam into the new beam, which has one-half the wavelength of the incident beam.
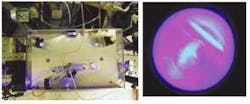
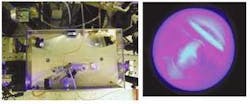
The prime application of SHG is the conversion of the fundamental wavelengths of solid-state neodymium (Nd3+) or ytterbium (Yb3+) infrared lasers to produce green output. SHG enables the desirable characteristics of these lasers— low power consumption and compact size— to benefit sources for visible wavelengths. SHG has led to the emergence of diode-pumped frequency-doubled lasers as the preeminent lasers in the scientific marketplace (see Fig. 1).
null
Second-harmonic generation is also used to generate coherent radiation at wavelengths where fundamental sources are lacking, such as in the ultraviolet. The interest in materials for frequency conversion below 200 nm possibly eclipses the search for fundamental sources at these wavelengths (the "fundamental" beam in this case would typically be the already doubled output of a solid-state laser). In addition, SHG greatly extends the range of tunable sources such as OPOs.
Inside or out?
Clearly, a high nonlinear response in the crystal is important for achieving efficient doubling. The specifications for nonlinear crystals take advantage of natural symmetries to simplify the susceptibility term—a third-rank complex tensor—to an effective nonlinear coefficient deff. In place of the 27 tensor components, there are typically two or three values of deff for materials of interest. These two or three values depend on the direction and polarization of the beams with respect to the crystalline axes.
A second critical factor for practical SHG is the need for high peak power in the fundamental beam. The scale of nonlinear coefficients is very small, but conversion efficiency increases as the square of the fundamental power. SHG was first observed at the University of Michigan (Ann Arbor, MI) in 1961. In this regard, it is fortunate that the first laser was a ruby laser, which has a pulsed beam with significant peak power.
Pulsed lasers, such as Q-switched and modelocked lasers, can produce high peak powers even if their average powers are modest. These peak powers yield high efficiency in a single pass through the SHG crystal, allowing it simply to be placed outside of the laser. For lower-power lasers, it may be necessary to build up the fundamental power by placing the crystal in an optical cavity that is matched to the modes of the fundamental beam.
The doubling crystal can be placed inside the laser cavity itself to take advantage of the circulating power in a continuous-wave laser, which can be 100 times greater than its output. Such a design must counteract the "green problem," in which the SHG crystal causes large amplitude fluctuations by swapping energy between polarization modes of the crystal. The green problem is avoided either by operating the fundamental laser in single longitudinal mode, or with a great many such modes.
Keep it together
The distance in the crystal over which the fundamental beam and its harmonic interact is also a critical factor. Dispersion causes the fundamental and the second harmonic beams to propagate at different speeds. As a result, the beams will interfere destructively after travelling a distance inside the crystal called the "coherence length," which is usually on the order of 10 µm. If the crystal length happens to be an odd multiple of the coherence length, no second-harmonic light will be emitted.
Techniques to overcome this destructive interference are known as "phase-matching." Phase-matching can be thought of as the need to satisfy the conservation of momentum, and is a requirement for nonlinear phenomena in general. (The exceptions are nonlinear absorption phenomena, such as Raman scattering.)
Phase-matching in nonlinear crystals makes use of their birefringence to negate the effects of dispersion. In the crystals used for SHG, birefringence means that a beam polarized in the direction of the optic axis (the "ordinary ray") will experience the same refractive index regardless of its direction of propagation. However, a beam polarized orthogonally to the ordinary beam (the "extraordinary ray") will find that the refractive index very much depends on its direction of travel in the crystal.
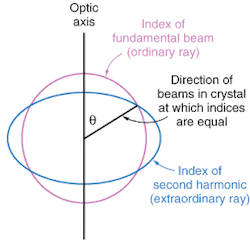
The optic axis is the direction along which these two refractive indices are the same when the beams have the same wavelength. When two beams differ in wavelength, dispersion makes their refractive indices different; the indices can be equalized by making use of variations in the extraordinary index. There are two methods of making the indices match.
How it's done
The first method relies on the angular dependence of the extraordinary index. The crystal is oriented so that its optic axis is in the plane of the polarization of the fundamental beam (making it the ordinary ray). The crystal is then set at the angle at which the extraordinary index for the wavelength of the second harmonic is equal to the ordinary index for the fundamental (see Fig. 2). The fundamental and second harmonic in this method are orthogonally polarized, which is a characteristic of birefringent phase-matching, not SHG in general.
null
An additional difficulty is that the energy of the two beams will propagate in different directions, a condition referred to as "Poynting vector walk-off." While large differences in the refractive indices are potentially desirable for phase-matching, the greater the birefringence in a material, the greater the walk-off problem. However, if the angle between the direction of propagation and the optic axis can be set to 90°, the angle between the Poynting vectors for the two beams is zero. This so-called "noncritical phase-matching" maximizes the length of nonlinear interaction on the crystal.
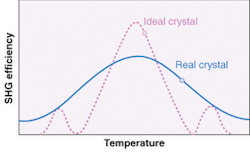
The second basic method of birefringent phase-matching relies on the dependence of the extraordinary index on temperature. Relatively modest heating, to about 300°C, can make the ordinary and extraordinary indices of a crystal such as lithium triborate (LBO) equal for the fundamental and harmonic beams (see Fig. 3). This effect, called "temperature-tuning," was first discovered by accident in lithium niobate (LiNbO3).
null
The ability of LBO and its cousin, beta barium borate (BBO), to achieve temperature-tuned noncritical phase-matching is one of the reasons for their increase in popularity for SHG in high-end systems. Other factors are their high damage thresholds and wide transparency range. Neither crystal, however, possesses exceptional values for deff.
The popularity of LBO and BBO shows that SHG has aspects of an art. Designing for SHG is not simply a matter of making the beam as intense as possible and choosing a crystal with the highest deff.
It is possible to circumvent the need for phase-matching in some circumstances by using specially fabricated crystalline structures. Some ferroelectric nonlinear materials, such as lithium niobate, can be fabricated with alternating layers of reversed crystalline orientation that are as thick as the coherence length. Such "quasi-phase-matched" structures, while somewhat limited in application, can exceed the performance of conventionally phase-matched crystals.
In addition to LBO and BBO, materials used for frequency doubling to wavelengths in and near the visible include potassium titanyl phosphate (KTP), and potassium niobate (KNbO3), which has the largest deff of all commercially available materials. The older materials KDP (potassium dihydrogen phosphate) and its KD*P isomorph still find some use.
Silver gallium sulfide (AgGaS2) is used as a doubling crystal for infrared radiation such as the 10.6-µm output of CO2 lasers. Adding cesium to LBO (CLBO) extends its tranparency further into the ultraviolet, and this material is slowly gaining wider acceptance despite some handling difficulties. Some of the most intense optoelectronic material research is directed at organic nonlinear materials, which have values of deff orders of magnitude greater than conventional crystals. These materials hold out the promise of SHG using smaller, lower-power, and less-expensive lasers.
Next month: Third-harmonic generation.