Special effects
As dramatic as they might be, the phenomena of second-order nonlinear optics (NLO) seem intuitive once they become familiar. The situation changes when a third incident beam is added. Third-order NLO phenomena encompass a wide range of interesting, useful, and sometimes even bizarre optical effects.
Fully nonlinear
The aspect of third-order NLO effects that makes them so distinct is the manner in which the third-order coefficients allow the beam to change the material itself. Recall that the third-order polarization response of the material is proportional to
P(3) µ Χ(3)Ea cos(ωat) Eb cos(ωbt) Ec cos(ωct) (1)
where the nonlinear susceptibility Χ(3) describes all of the optical response of the material. This polarization is responsible for generating a new light wave, so there are really four waves in total. For example, if all three incident waves a, b, and c have the same frequency (that is, they are really the incident same beam) then equation 1 describes a frequency-tripled output beam.
Some of the many cross terms that are possible in a full expansion of equation 1 can be grouped together so that the index of refraction, which is included in the susceptibility, becomes n = n0 + Χ(3)E2. Then n appears deceptively simple:
n = n0 + n2I (2)
where n0 is the linear index of refraction and I is the intensity of the beam. The intensity of most beams varies radially across the profile, and if a beam is pulsed, it will vary in time as well. As a result, for very intense beams, the index of refraction of an otherwise uniform dielectric can be made to vary in space and time.
While second-order NLO phenomena require that the nonlinear material lack certain symmetry properties, this is not the case for third-order effects. These can occur in any material, even glass of the highest purity. Together with the tight confinement and very long interaction lengths in fiber, this makes a number of third-order NLO effects, such as stimulated scattering and four-wave mixing, critical to the performance of optical networks.
Self-focusing
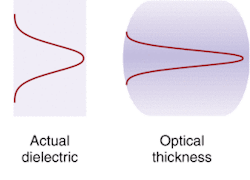
The spatial variation of n across the profile of an intense beam can cause what is known as self-focusing in a dielectric. The index of refraction increases toward the center of the beam, and usually toward the center of the dielectric itself, which causes the material to behave as a positive lens (see Fig. 1). This directs the outer portions of the beam inwards, further increasing its central intensity.
It is easy to see how this can lead to runaway optical damage. Because all materials exhibit third-order effects, self-focusing can even occur in a flat plate of glass. The most common result of self-focusing is a dark streak of damage in an optic. In a high-power laser system, self-focusing can cause the beam to collapse within the laser rod itself, with catastrophic results.
The situation is more complicated when self-focusing causes the beam to intensify in a nonuniform profile. Small ripples in the wavefront grow exponentially when the intensity exceeds a critical value. The same concept applies in the time domain, causing a continuous-wave beam to spontaneously break up into a pulsed sequence.
Self-focusing in ultrafast systems
A clever method of circumventing damage from self-focusing in high-peak-power ultrafast systems was developed in the 1980s by researchers at the University of Michigan (Ann Arbor, MI). "Chirped-pulse amplification" first reduces peak power by using dispersion to greatly lengthen the duration of a pulse before it is amplified. After the energy level of the pulse has been increased, often by a factor greater than 106, the dispersion is reversed using robust optics to recompress the pulse back to ultrafast durations.
Self-focusing is essential, on the other hand, to the success of most ultrafast systems, which are based on modelocked Ti:sapphire lasers. It was originally thought that modelocking Ti:sapphire would be difficult, so it was surprising when such lasers were observed to modelock spontaneously. Researchers at the University of St. Andrews (Scotland) first explained this phenomenon in the 1990s.
Focusing the beam in a Ti:sapphire crystal causes its center to intensify further, and it may separate into a train of pulses. An aperture in the cavity (such as the diameter of the rod itself) will preferentially induce more loss for the edge of the beam, which is still continuous wave, allowing the pulsed central portion to monopolize the laser gain. A variety of NLO phenomena, including self-focusing, are referred to as the "Kerr effect" after the 19th century Scottish physicist, and modelocking in Ti:sapphire has come to be known as Kerr-lens modelocking.
The silver lining
The Rayleigh range is a measure of the distance over which a laser beam remains collimated, and is typically proportional to the area of its cross section. Accordingly, micron-sized beams diffuse significantly over just a few centimeters of travel. But in the 1990s, researchers discovered that intense pulses only microns in diameter can form a filament of light that propagates through air for hundreds of meters.
In this effect, self-focusing first forms a positive lens in the air then this high-intensity focus ionizes the air molecules. The ionized air has a lower index of refraction and causes the pulse to spread out. When a balance is achieved between focusing and spreading, the beam is described as "self-guiding."
Researchers in Germany and France are investigating self-guided filaments to improve lidar spectroscopy of atmospheric pollutants. Other NLO effects act to broaden the spectrum of the filament from the ultraviolet to the infrared. The broad spectrum and preferential scattering properties of the filament allow simultaneous detection of multiple pollutants and better resolution compared to traditional lidar.
Physicists at the Ecole Polytechnique (Palaiseau, France) have found that self-guided pulses can be formed in solids as well as gases. The optical density of glass is orders of magnitude greater than that of air, but the same effects can occur if the initial focus of the high intensity pulse is precisely controlled (see Fig. 2). Researchers postulate that the effect may be useful in optical computing, and may lead to a superior technique for generating ultrafast pulses.
Self-phase modulation
The equivalent of self-focusing in the time domain is self-phase modulation (SPM). When a high-peak-power ultrafast pulse propagates through a dielectric material, it experiences an increasing index of refraction as the pulse reaches its peak. The central portion of the pulse slows, allowing the leading edge to speed ahead, while the trailing edge catches up. The Fourier component wavelengths at the leading edge are shifted toward the red, and the trailing edge of the pulse is "blue-shifted."
Self-phase modulation thus adds new frequencies to the pulse, as well as a variable frequency component, a phenomenon called "chirp." In ultrafast systems, SPM will cause the pulse to broaden with each pass through the laser rod as it circulates in the cavity. Dispersion compensation, which uses optical elements such as gratings or prisms to correct for SPM, is critical to the design of these systems.
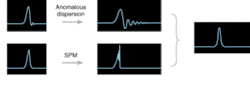
Dispersion will ordinarily cause the pulse to increase in duration. This is true for so-called "normal dispersion," where n increases as λ decreases and the bluer components of the pulse travel slower than the redder wavelengths. However when combined with a particular type of dispersion, SPM can be used to form a pulse that remains unchanged as it propagates.
Near an absorption band in a material, the dependence of the index of refraction on wavelength reverses direction. The material is said to be anomalously dispersive—n decreases as λ decreases. Now, for an intense pulse, SPM produces a red-shifted leading edge that propagates more slowly then the blue-shifted trailing edge. The net result is that the pulse is compressed.
Solitons
When these effects just balance, the result is a pulse that travels without spreading (see Fig. 3). This is called an optical soliton. In reality, other effects, such as group velocity dispersion, add to the broadening or the compression of the pulse as well, but the principal remains the same.
A soliton, or a "solitary wave," has many fascinating physical and mathematical properties. When two solitons collide, for example, they either repel each other or combine, depending on their relative phase. It is easy to see that this interaction can form the basis, at least in principle, of an optical computer.
Solitons propagate unchanged in one or more spatial dimensions, or in time (or some combination) within a nonlinear medium. Because they rely on a third-order NLO effect, this medium can be an ordinary optical fiber. The fiber already confines the light tightly in cross section, and temporal solitons can travel unchanged over many kilometers without distortion, making them a topic of much interest in telecommunications.
Solitons can have durations on the order of femtoseconds, and so are of interest to researchers hoping to improve fiber lasers as an alternative to conventional ultrafast systems. Fiber lasers are superior in size and are more robust, but they produce longer pulses at significantly lower energies. Improving their performance has been limited by nonlinearities in the fiber itself, but better understanding and control of soliton pulses in fiber lasers may help overcome these hurdles.
A soliton that fully preserves its shape in space and in time is called a "light bullet," and in the manner of a bullet, travels through space undiffracted and undistorted by absorption. Researchers at Cornell University (Ithaca, NY), the University of Colorado (Boulder, CO), and elsewhere are seeking the right combination of nonlinear material properties and pulse shaping to produce such an object.
The cutting edge
The principles of self-focusing and SPM are central to third-order effects in which the energy of the material remains unchanged (inelastic phenomena will be discussed in a future article in this series). These effects include counter-intuitive phenomena such as optical phase conjugation and optical bistability, and equally exotic applications, such as real-time holography.
Next month's article in this series examines some of the ways nonlinear optics can be used to control laser beams.