Special effects

The field of nonlinear optics has revolutionized the applications of laser light. New developments may make nonlinear devices commonplace.

After decades of painstaking development, the first commercial applications of nonlinear optics are now mature technologies. Systems based on second-harmonic generation, frequency tripling and quadrupling, and even parametric amplification are priced competitively. Research efforts in other areas, some ongoing since the early days of laser development, remain intense. Two areas that have evolved in a manner not predicted in their early history are optical bistability and optical phase conjugation.

A heuristic device

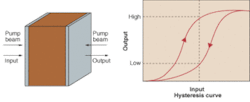
To illustrate optical bistability, first recall that a Fabry-Perot cavity is formed by two facing mirrors that trap light at wavelengths resonant with the mirror spacing. Depending on the reflectivity of the mirrors, the light circulating within the cavity builds up to an intensity that is much greater than the incident light, resulting in a substantial transmission at wavelengths where the mirrors are almost completely reflective. For intensities at conventional values, the fraction of light transmitted is independent of the incident intensity.

Now consider what happens when the cavity is filled with a nonlinear optical material. In the standard model, this material is a saturable absorber, a nonlinear material that has an upper limit on the amount of light power it can absorb. Above this limit, the material "bleaches," becoming transparent.

As the intensity incident on the cavity is increased, at first the light trapped between the mirrors is not enhanced, in contrast to the behavior of a conventional Fabry-Perot cavity at resonance. The absorbing medium produces sizable losses, dampening the effect.

When the saturation limit is exceeded, the circulating intensity begins to rise, causing further bleaching of the absorber, which further increases the circulating intensity, and so on. The transmitted intensity will then jump discontinuously to a much higher value, one that is characteristic of the absorber being fully saturated (essentially absent).

If the incident intensity is then reduced, the absorber will remain transparent for intensities much lower than required for bleaching when the incident intensity was increasing. This is because the already saturated absorber in the cavity allows the circulating intensity to achieve high resonant levels. As the incident intensity continues to fall, at some point the bleaching of the absorber will weaken, the circulating intensity will drop, and the transmitted intensity will fall discontinuously to a much lower value.

This behavior is described by a hysteresis curve (see Fig. 1). More realistic systems used to study or apply optical bistability might use an electro-optic crystal or some nonlinear dispersive material in the cavity. The physics of these systems is different from, but analogous to, the behavior of the saturable absorber device. For example, many of the properties of a photonic crystal device, so-called "holey fiber," are described by optical bistability.

A light touch

The practical significance of bistability is the control of light by means of light in such applications as optical switching, optical transistors, and so on. Devices using optical bistability may be the ultimate components of all-optical networks, optical computers, and storage networks. Major progress will be made toward these ends when a much faster dynamic response is achieved than is currently possible.

If the incident beam for our saturable absorber device is thought of as a control beam, and a second beam, the signal, is also incident on the cavity, then the use of such a device as a switch or element in a binary circuit is readily understood. If the signal arrives with an intensity that falls between the two discontinuities of the hysteresis loop, then there are two possible output values that can result. The switch is open and the signal is transmitted if the absorber is on the upper branch, and the switch is closed for the lower branch.

The behavior of bistable (or multistable systems) is very rich, and its study is extremely helpful for systems that display nonlinear and chaotic response. If the incident intensity is changed suddenly to a value from below to above the jump discontinuity, our model device may spontaneously produce a train of pulsed output from a continuous input beam. This is reminiscent of the behavior of single-mode optical fiber when the level of a continuous-wave signal approaches the nonlinear regime of silica.

The answer in code

As another example, the output of semiconductor lasers is extremely sensitive to feedback. Reflections of less than one part in a million can cause the laser to produce complex, random output. The laser can shut off entirely for tens of nanoseconds, spaced at intervals ranging from nanoseconds up to milliseconds, and emitting a train of pulses picoseconds in duration while it is on.

These instabilities are deleterious for many applications, such as optical disc devices, but they can also be put to good use. It happens that the output of a laser can be synchronized to follow the output of another laser that is behaving chaotically, a result that was predicted theoretically in 1990 by Pecora and Carroll at the Naval Research Laboratory (Washington, D.C.). This effect is under study for use in fast, secure optical communications.

Chaotic communications, using this phrase in a positive sense, mixes a message signal with the output from a chaotic laser (see photo, p. 64). The amplitude of the message is kept smaller than the average fluctuations of the laser, making it impossible to distinguish the message from the chaotic carrier. To recover the message, the signal is compared to the output of another chaotic laser at the receiving end, which is synchronized to the transmitter.

Optical phase conjugation

Ever since it was first observed by Russian researchers in 1972, optical phase conjugation (OPC) has excited speculation about its revolutionary potential. The first observation resulted from stimulated Brillouin scattering. An understanding of OPC was delayed until it was produced using four-wave mixing, and although a surprising variety of nonlinear effects can be used, four-wave mixing remains the most straightforward way to study OPC.

Degenerate four-wave mixing occurs, in this case, when three incident beams combine to produce one new beam, all of the same frequency. Two pump beams are combined in a nonlinear crystal such as barium titanate (BaTiO₃) to create an intensity-dependent phase grating. The arrival of a third wave at the grating, the probe beam, results in the production of the new phase-conjugate beam.

To efficiently produce the grating, the pump beams must be phase-matched, a consequence of the requirement for the conservation of momentum. This requires these two beams be equal and opposite in direction. Phase matching also applies to the probe beam and the beam newly generated by four-wave mixing, and results directly in its phase-conjugate nature.

Simple but strange

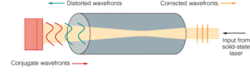
Phase conjugation can be thought of as creating a mirror with very unusual properties. Unlike a conventional mirror, which only reverses the tangential component of an incident beam, a phase-conjugate mirror (PCM) retroreflects the complete incident beam back to its origin, regardless of the angle at which it arrives. Moreover, the phase of the new beam is the conjugate of the incident wave. Ideally, then, the new wave looks like the probe beam traveling backward in time.

The most well-known aspect of OPC is its ability to reverse the degradation suffered by an image that is transmitted through a distorting medium. Early demonstrations of this effect used an etched piece of glass as the distorting medium—seen in person, the effect is almost magical. A laboratory application of a PCM is to reverse the distortions typically experienced in a solid-state laser system that uses a high-power amplifier stage (see Fig. 2).

Clear memory

Optical phase conjugation figures into development efforts for optical data storage. To reliably retrieve data stored in volumetric holograms, the optical system must be free of aberrations over a large field of view. Researchers at IBM (San Jose, CA) and elsewhere are looking into the possibility of circumventing this requirement by forming the retrieval beam using a PCM formed in a nonlinear crystal.

An advantage to generating OPC using four-wave mixing (compared to other nonlinear methods) is that the signal or image can be of relatively low intensity, because the pump beams power the effect. Likewise, it is possible for OPC using four-wave mixing to amplify the conjugate image, producing an effective reflectivity greater than unity.

Despite its exciting possibilities, more than 30 years after its discovery there are hardly any commercial applications based directly on OPC. In view of the quantity of research that has been done in the field, this result is disappointing. There are many problems related to the properties of the nonlinear materials used for phase conjugation, including the slow response time for the effect, often in the millisecond range.

The cutting edge of NLO

Earlier articles in this series described other areas of active research in nonlinear optics, including higher harmonic generation to produce soft x-rays, the production of ultrafast pulses, nonlinear spectroscopy, applications in optical networking, including the generation of soliton pulses, research into holey fiber, and new nonlinear materials, including organic crystals. Other areas of active research include quantum statistics, the nonlinear effects of quantum confinement, and the use of the photorefractive effect in adaptive neural networks.

One can anticipate that the development of new nonlinear materials has particular promise. Some of these new materials may reduce the threshold for nonlinear effects down to conventional light levels, and complete the evolution of nonlinear optics from the exotic to the commonplace.