Reflection grisms compensate dispersion in ultrafast systems
STEVE KANE, JEFF SQUIER, RALPH JIMENEZ, LYUBA KUZNETSOVA, FRANK WISE, HENRY KAPTEYN, and BRUNO TOUZET
Whenever an ultrafast laser pulse is propagated through material—an optical fiber, a focusing objective in a microscopy system, or even the gain medium in the laser that generated or amplified the pulse in the first place—the wavelength-dependent refractive index of the material distorts the temporal shape of the pulse and reduces its peak power. Compensation of this material dispersion is a fundamental aspect of nearly all ultrafast optical systems, from the production of pulses to the delivery of pulses to experiments and applications. Broadening of the pulse by material dispersion is sometimes intentional and desirable, and sometimes it is an unwelcome consequence of the optical system. However, the ultimate goal is always the same: to eventually propagate the pulse through a compensating optical system—a pulse compressor—whose wavelength-dependent path length is opposite that of the dispersive material, resulting in a fully compressed, high-peak-power pulse at the pulse’s final destination.
Traditional pulse compressors are based on pairs of diffraction gratings or prisms, and both types of compressors have limited value for compensating material dispersion. Grating-pair compressors can imperfectly compensate for large amounts of material dispersion, and prism pairs can nearly perfectly compensate for only tiny amounts of material dispersion. Until recently there have been no practical solutions to the problem of completely compensating modest to large (1 to 500 m) amounts of dispersive material. Over the past year we have developed and demonstrated a new class of pulse compressors based on reflection grisms—metal-coated diffraction gratings coupled to prisms—that fully compensate material dispersion (see Fig. 1). These grisms have been demonstrated in Ti:sapphire laser systems at 800 nm and at 1030 nm in ytterbium (Yb)-doped fiber systems with equal success, producing transform-limited pulses after propagation through meters of dispersive material.
Dispersion in materials and pulse compressors
Any dispersive system—either a material with a wavelength-dependent index or a pulse compressor with a wavelength-dependent optical path—imparts a delay to a pulse that can be expressed as a function of wavelength (or more conveniently, frequency). A delay that is linear with frequency is called group-delay dispersion (GDD); a delay that is quadratic with frequency is termed third-order dispersion (TOD). When a pulse experiences GDD, it is symmetrically stretched in time (for example, a short Gaussian pulse will simply become a longer Gaussian pulse), and if it sees TOD, the pulse is asymmetrically distorted with a series of prepulses or postpulses. Group-delay dispersion and TOD can be either positive or negative in sign; for example, a system with positive GDD (like glass) has a longer optical path length for blue wavelengths than red wavelengths. After a pulse travels through a positive-sign GDD system, the only way to recover the original short pulse is to propagate through another system with GDD of identical magnitude but negative sign (having a longer path length for red wavelengths than blue wavelengths). Sending a pulse through a series of opposite-signed dispersive systems is the essence of femtosecond pulse compression.
For ultrashort pulses, especially those that have suffered a great deal of dispersion, it is necessary not only to compensate for the GDD, but also the TOD. If left uncompensated, leftover TOD will prevent the pulse from being compressed to its ideal, transform-limited duration.
The magnitude and sign of GDD and TOD of materials is determined by the wavelength-dependence of the refractive index and the amount of material through which the pulse propagates. For all optical materials in the 700-to-1100 nm wavelength range, GDD is always positive in sign, and TOD is always positive in sign. There are no exceptions to this rule among optical glasses and common crystalline materials (Ti:sapphire, TeO2, LiSAF, YAG, and so on.); whenever a pulse propagates through any optical material, it always accumulates positive GDD and positive TOD.
To compensate for material dispersion, it is therefore necessary to find a pulse compressor with negative GDD and negative TOD in the same proportions. Can this be done? The most common pulse compressor is the Treacy grating pair, which was shown in 1969 to have negative GDD. The exact dispersion of the grating-pair compressor is determined by several factors (grating line density, incidence angle, grating separation), but it is straightforward to prove that, for any configuration of a Treacy compressor, the GDD is always negative and the TOD is always positive. There is no way to arrange a grating pair to provide negative GDD and negative TOD, which would be necessary to compensate for material dispersion.
Another commonly used pulse compressor is a sequence of prisms, which provide negative GDD in a variety of applications. In addition, a prism pair can be arranged (by choosing the proper prism materials and usage geometry) to have negative GDD and negative TOD, ideal for compensating material. For example, the well-known 6 fs pulses produced at Bell Labs in the 1980s were compressed using a prism sequence to remove excess TOD. However, the usefulness of prisms is limited: in general, compensation of a single centimeter of material requires a prism spacing of about 10 cm. As the material path lengths in the system become long (as in the case of a fiber-delivery system or a regenerative amplifier) a prism sequence becomes entirely impractical for material-dispersion compensation.
In the early 1990s P. Tournois demonstrated a method for compensating tens of meters of material, which was further refined by two of us (Steve Kane and Jeff Squier).1, 2 Tournois showed that a Treacy-style pulse compressor using traditional grisms—transmission gratings engraved directly onto the surface of prisms—would yield a dispersive system with zero TOD. In 1995 we demonstrated experimentally that transmission grisms could be designed and fabricated to give large amounts of negative GDD and negative TOD in the proper proportions for compensating material dispersion; we used these grisms to compress 800 nm, 130 fs pulses after propagation through 100 m of fiber.
This early demonstration of material-dispersion compensation using grisms was interesting, but not of great practical significance. The transmission grisms were very inefficient (25% or less transmission per pass), and it was easy to show that the required geometry for material-dispersion compensation was totally incompatible with the efficiency constraints of diffraction gratings. The hope of using traditional grisms for dispersion compensation and pulse compression quickly faded.
Grisms revisited
The need for a material-dispersion compensator continued to increase, however, especially with the growth of ultrafast fiber lasers. Ten years after the original grism experiments, we began to investigate additional design parameters that might overcome the shortcomings of the original grisms and allow us to produce a pulse compressor with the proper GDD, TOD, and diffraction efficiency for practical use. The result was a grism consisting of a reflection grating mounted to a prism, with a critical design difference as compared to traditional grisms. After diffracting from the grating, the pulse propagates through the prism material, and then refracts out of the prism at an air-glass interface that is tilted by a large angle with respect to the grating. This new parameter—the angle of the prism with respect to the diffracted beam—allows us to design reflection grisms at near-Littrow usage, which is the ideal condition for high diffraction efficiency.
By carefully optimizing the grism parameters, we have been able to produce pulse-compression grisms with proven groove densities (600, 1200, 1480 lines/mm) and standard prism geometries and materials. A well-designed grism can exhibit 90% efficiency, which is competitive with the best pulse compression-grating specifications on the market. A patent application has been filed for the use of these new grisms as compensators for material dispersion.3
Applications at 800 nm
A novel technique for producing very high-average-power amplified pulses is downchirped pulse amplification (DPA), introduced in 2004. In DPA, pulses are stretched by a grating-based delay line, amplified in Ti:sapphire, and then compressed by propagating through 1 to 2 m of dispersive glass.4 Contrary to conventional chirped-pulse amplification, a DPA system relies on the negative GDD of gratings to stretch the pulse, and the positive GDD of material to compress it. For relatively modest pulse energies, this technique yields extremely high throughput from the compressor, reduces spatial chirp, and is exceedingly simple to align. To produce ultrashort amplified pulses, however, it is necessary to have a stretcher whose GDD and TOD are perfectly matched to the dispersive material in the compressor. Reflection grisms are a natural fit for this application.Using 600 lines/mm gratings and off-the-shelf BK7 prisms as stretcher grisms, pulses as short as 35 fs were obtained after compression through 120 cm of SF18 glass (see Fig. 2).5 Losses in the compressor are limited by surface reflections, which can be reduced by antireflection coatings to levels an order of magnitude more favorable than conventional compressors. Reflection-grism pairs are extremely compact—the two-grism system was less than 7 cm long and compensated nearly 200,000 fs2 of GDD and 120,000 fs3 of TOD.
Fiber applications at 1030 nm
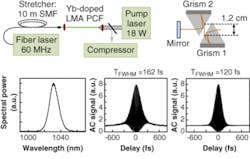
In Yb-doped fiber-laser systems, an ultrashort pulse propagates through a very large amount of dispersive fiber during all stages of the generation and amplification process. Recently we demonstrated a chirped-pulse-amplification system using a 10 m fiber stretcher and a Yb-doped fiber amplifier, with reflection grisms as the pulse compressor.6 These grisms were specifically designed to compensate the large amounts of TOD present at 1030 nm, and were able to fully compensate for 10 m of fiber (with a grism spacing of only 1.2 cm). This system was gain-narrowing-limited to 120 fs pulses, and the extremely clean interferometric autocorrelations indicate full GDD and TOD compensation by the grisms (see Fig. 3). These initial results have encouraged us to build a high-power CPA system with a 400 m fiber stretcher; these experiments are planned for spring 2007.In addition to fiber-laser applications, reflection grisms will be very useful in applications (such as multiphoton microscopy) that would benefit from fiber delivery of femtosecond pulses.
REFERENCES
1. P. Tournois, Electronics Lett. 29, 1414 (1993).
2. S. Kane and J. Squier, IEEE J. Quantum Electron. 31, 2052 (1995).
3. S. Kane, “Grating with angled output prism face for providing wavelength dependent group delay,” US Patent Application (2006).
4. H.C. Kapteyn and S.J. Backus, “Downchirped pulse amplification,” U.S. Patent 7,072,101, July 4, 2006.
5. D. Gaudiosi et al., Optics Express 14, 9277 (2006).
6. L. Kuznetsova et al., Advanced Solid-State Photonics 2007, Vancouver, Canada, paper TuB3 (2007).
Steve Kane and Bruno Touzet are with the Diffraction Gratings Division of Horiba Jobin Yvon, 3880 Park Ave, Edison, NJ 08820; e-mail: [email protected]; www.jobinyvon.com/grisms. Jeff Squier is with the Colorado School of Mines, Golden, CO 80401; Ralph Jimenez is with the National Institute of Standards and Technology, 325 Broadway, Boulder, CO 80305, and the University of Colorado, Boulder, CO 80309; Lyuba Kuznetsova and Frank Wise are with Cornell University, Ithaca, NY 14853; and Henry Kapteyn is at the University of Colorado, Boulder.