Lens tolerances: Software eliminates the guesswork
DONALD C. DILWORTH
Some years ago I designed a small high-resolution projection lens. The tolerances were tight, and some elements had to be centered to within 10 µm. The drawings went to an offshore company, and when the lenses came back they did not work. The vendor had designed the cell in two parts that screwed together, but the threads were not concentric with the lenses. You could feel the decenter with your fingers in some cases. I reported the error to the shop, but they replied angrily, insulted that I had criticized their work. Another time, lenses came back from a shop and did not work properly. After two months of strenuous denial, the shop finally admitted that the parts were far out of spec.
While we do not expect lens manufacturers to be skilled mathematicians, they need to understand that there is a science behind the tolerances on the drawings. These examples show that some do not. They are not entirely to blame.
Before the development of modern lens-design software, designers assigned tolerances to lens dimensions following a rule-of-thumb procedure involving more guesswork than calculation. A few still do. Some designers calculate tolerances by first getting inverse sensitivities, which give the amount by which each variable can be in error and still meet the performance specifications. Then they divide those numbers by the square root of the total number of variables, and that is the budget.
This procedure is better than the rule-of-thumb approach, but still not rigorous by modern standards. That budget is proper only in cases where one would invariably find each parameter in error by exactly the assigned tolerance. Because lens parameters are most often somewhere within their range—but not exactly at the edge—a budget derived with that approach invariably assigns tolerances that are tighter than they need to be. When a shop makes an element that exceeds the tolerances created in this way, and the lens works well, the lens maker is inclined to conclude that tolerances need not be closely adhered to in other projects. This is a mistake.
Modern practice
Modern tolerances, by contrast, calculated by a state-of-the art lens-design program such as SYNOPSYS, are more sophisticated. This software first identifies all of the parameters that are to go into the budget and the quality descriptors that define the imaging goals. Then the rules of statistics tell us that, if we know the mean value and standard deviation of each parameter, we also know the mean value and standard deviation of each of the quality descriptors.
The procedure is rigorous under certain conditions, and the output from the program is a table of the tolerances. Thus, we know, for example, that if a lens were built to that table, then the Strehl ratio everywhere in the field would be higher than, say, 0.7, to a confidence level of 2, which means that we could predict that 97.7% of a large batch of lenses would have a larger Strehl ratio. Gone is the guesswork behind a lens tolerance budget.
A further refinement results from giving the software a definition of what constitutes a “tight” tolerance. Any tolerance that wants to be tighter than that will be loosened somewhat by the program, with most others getting tighter to compensate. This procedure reduces overall cost. Because the definition of loose and tight are more or less the same throughout the precision-lens industry, even without close collaboration with the shop the designer can usually generate a low-cost budget rather well.
But we mentioned “certain conditions.” Here is where the vendor can help to meet the error budget—or derail the whole procedure. For the budget to be valid, two criteria must be met: first, the mean value of each parameter must be at the design value and, second, the parameter must be equally likely to be found anywhere within its error bracket.
Let us look at how some shops deviate from these statistical assumptions. First, consider the case in which a testplate was poorly measured. The print calls out a radius, with a tolerance, and when the testplate is measured more carefully it is found to be different from the assumed value—but the error is still within the tolerance budget. Does one make the lens to that testplate? Most shops would say yes, because the radius is within tolerance. But clearly, this violates the first condition above: the mean value will be the remeasured value, not the design value.
I am astonished by how many shops keep a poorly measured testplate list, which requires a user to ask for each testplate to be remeasured, and then reoptimize the lens to the new values. Sometimes new testplates are needed and the whole procedure repeated, driving up design costs.
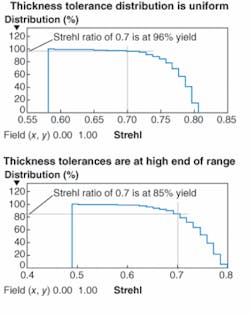
Yet another issue involves element thicknesses. Many shops aim for the high end of the tolerance budget so that, if the part requires reworking, the thickness is less likely to go under. This of course also violates the statistics. In a lens in which the thickness errors are uniformly distributed, the desired Strehl ratio is achieved quite well, but if the thicknesses are all at the high end of their range the yield is significantly poorer—even though, on paper, all tolerances are met (see figure).
One could better obtain the desired results by recognizing that the thicknesses conform to different statistics. One wants the standard deviation of the thickness to be the same as with the uniform distribution, and this will occur if the thickness tolerances are divided by the square root of three for this case. Then the expected value of the thickness error will be the same as for the uniform distribution, and the yield improves. Few shops understand this kind of subtlety.
Success in optics requires close collaboration with the vendor, who must understand the significance of the issues presented here. If the designer can connect with the shop to this degree, there will be fewer instances of lenses that do not work as they should. Designers should spell out these considerations when approaching a vendor to ensure that ignorance is no longer an excuse for the failure of a project.
Donald C. Dilworth is president of Optical Systems Design, P.O. Box 247, East Boothbay, ME 04544; e-mail: [email protected]; www.osdoptics.com.