Computer-based design programs are now the standard design tool for optimization of imaging systems such as camera lenses and telescopes. Depending on the program, the typical procedure begins with the design of a basic optical system and its approximate operation. The user then defines a “merit function” to constrain the desired performance of the system, and designates which parameters of the initial design are variable. The program then varies these parameters so as to drive the merit function to its optimal value.
Because of their much greater generality, nonimaging systems (or nonsequential systems, as they are known in the jargon of ray-tracing) can be much harder to optimize. There are many reasons: generally, nonsequential systems must be traced with many more rays than sequential imaging systems require, and the ray-tracing results are captured on pixelated detectors. Because ray-tracing results are “binned” into pixels, the construction of a merit function that is easily optimizable can be very difficult.
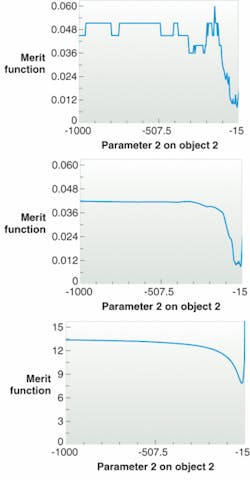
As an example, imagine the design of a mirror to produce the maximum on-axis brightness from a chosen commercially available light-emitting-diode (LED) source. The brightness of the LED integrated over the central degree or so is 25 candela (cd), and the optimization of the mirror is not simple because of the detailed spatial and angular structure of the LED source. The on-axis brightness of 10,000 rays varies when just the base radius of curvature of the mirror is varied (see figure). If the radius of curvature range were to begin at approximately -800, it would take a lot of numerical analysis to find the minimum at around -40.
A very simple answer to this problem is to simply trace more rays. The more rays that are traced, the smoother this plot will become. The smoother the merit function is, the easier it is to find a stable minimum. However, the time to perform the calculation increases linearly with the number of rays traced, so it is preferable to maximize the information obtained from fewer rays traced, rather than just tracing more rays.
Because the energy in a given ray is assigned only to one pixel, a small change in the system design will result in either the energy remaining in that pixel (so no change to the merit function) or, if the energy moves to a neighboring pixel, to a sudden jump. As a result, optimization is difficult, with discontinuous derivatives in the merit function occurring when a ray crosses the boundary into a new pixel.
A new method called pixel interpolation simplifies the optimization of the merit function in such designs. Instead of 100% of a ray’s energy being assigned to a single pixel, a fraction of the energy is spread to adjacent pixels around the primary ray-receiving pixel. As a result, any system tweak that causes a noticeable change in the merit function causes a ray to shift a pixel location. The resulting merit function is far smoother, with gradients that point to the region with minimized merit function and maximum on-axis brightness (see figure, center). This is accomplished using the same number of rays as the previous example.
Even more improvement can be obtained by making use of the moment-of-illumination data. The first moment of a grid of data is its centroid, and the second is its effective width. By defining the first angular moment of the detector data at (0, 0)-so that the beam of light is centered on-axis-and targeting the second angular moment to zero-so that the beam has a narrow distribution around zero-an even better merit function can be defined (see figure, bottom). Not only is this merit function smooth, but it has only a single minimum compared to the multiple minima of the previous functions, which greatly simplifies optimization.
The moment-of-illumination data is so useful because all the rays that hit the detector contribute to the merit function. In the first merit function, only those that land within a cone of a few degrees contribute. Pixel interpolation allows rays over a slightly larger angular range to contribute. But with the moment data, all rays contribute. For example, if a ray lands at 30°, a system change during optimization can make that ray now land at 29.9°. This change will contribute to the first and second moment data. Even in the absence of pixel interpolation, the moment data is smooth and has a well-defined gradient that points in the direction of the desired performance.
We have used the ZEMAX optical-system design program to perform an optimization over 22 variables in a free-form mirror. Using the first merit function, we improved the brightness of the LED from 25 to 250 cd, a tenfold increase. But the optimization took many hours because of the complexity and noisiness of the 22-variable merit function space. Using the third merit function, a better improvement was obtained from the same starting point in just a few minutes. The use of pixel interpolation and moment-of-illumination algorithms, such as those built into the latest release by ZEMAX, dramatically improves how optimization can be used in a wide range of illumination problems.
About the Author
Mark Nicholson
Vice President of Operations, Zemax
Mark Nicholson is vice president of operations at Zemax (Kirkland, WA).